| (5.21) |
Otherwise, if one thinks
there is a greater chance of the mass having
small rather than high values,
a prior which reflects
such an assumption could be chosen,
for example a half normal with
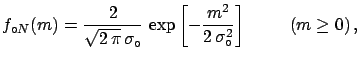
![$\displaystyle f_{\circ N}(m) =\frac{2}{\sqrt{2\,\pi}\,\sigma_\circ} \,\exp{\left[-\frac{m^2}{2\,\sigma_\circ^2}\right]} \hspace{1.0cm} (m \ge 0)\,,$](img687.png) |
(5.22) |
or a triangular distribution
| (5.23) |
Let us consider for simplicity the uniform distribution
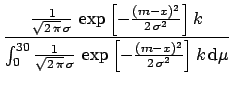 |
![$\displaystyle \frac{
\frac{1}{\sqrt{2\,\pi}\,\sigma}
\,\exp{\left[-\frac{(m-x)^...
...i}\,\sigma}
\,\exp{\left[-\frac{(m-x)^2}{2\,\sigma^2}\right]}
\,k\, \rm {d}\mu}$](img690.png) |
(5.24) | |
| (5.25) |
The value which has the highest degree of belief is
| (5.26) |
If we had assumed the other initial distributions the limit would have been in both cases
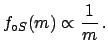 |
(5.27) |
practically the same (especially if compared with the experimental resolution of
| (5.28) |
To avoid singularities in the integral, let us take a power of
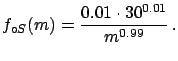 , and let us limit its domain
to 30, getting
, and let us limit its domain
to 30, getting
| (5.29) |
The upper limit becomes
| (5.30) |
Any experienced physicist would find this result ridiculous. The upper limit is less a
Instead, priors motivated by the positive attitude of the researchers
are much more stable, and even when the observation is ``very negative''
the result is stable, and one always gets a limit of the order of the
experimental resolution. Anyhow, it is also clear that when ![]() is several
is several ![]() below zero one starts to suspect
that ``something is wrong with the experiment'',
which formally corresponds to doubts about the likelihood itself.
below zero one starts to suspect
that ``something is wrong with the experiment'',
which formally corresponds to doubts about the likelihood itself.