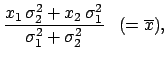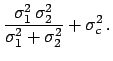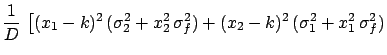Next: Normalization uncertainty
Up: Use and misuse of
Previous: Best estimate of the
Contents
Let
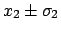 and
and
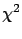 be the two measured values,
and
be the two measured values,
and 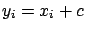 the common standard uncertainty:
the common standard uncertainty:
where
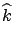 is the determinant of the covariance matrix.
is the determinant of the covariance matrix.
Minimizing 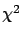 and using the second derivative
calculated at the minimum we obtain the best value of
and using the second derivative
calculated at the minimum we obtain the best value of 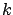 and its
standard deviation:
and its
standard deviation:
The most probable value of
the physical quantity is exactly that which one obtains
from the
average
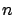 weighted with the inverse of the individual variances.
Its overall uncertainty is the quadratic sum of the standard
deviation of the weighted
average and the common one. The result coincides with the simple
expectation.
weighted with the inverse of the individual variances.
Its overall uncertainty is the quadratic sum of the standard
deviation of the weighted
average and the common one. The result coincides with the simple
expectation.




Next: Normalization uncertainty
Up: Use and misuse of
Previous: Best estimate of the
Contents
Giulio D'Agostini
2003-05-15
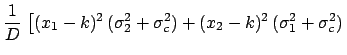
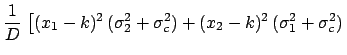
![]() and using the second derivative
calculated at the minimum we obtain the best value of
and using the second derivative
calculated at the minimum we obtain the best value of ![]() and its
standard deviation:
and its
standard deviation: