Well, this was meant to be a short note. Obviously
it is not just a comment to the New Scientist article,
that could have been contained in a couple of sentences.
In fact, discussing with several people, I felt that
yet another introduction to Bayesian reasoning,
not focused on physics issues, might be
useful.
So, at the end of the work, Columbo's cameras
were just an excuse.
Let us now summarize what we have learned
and make further comments on some important issues.
First, we have to be aware that often we do not see
`a fact' (e.g. Galesco killing his wife),
but we
infer it from other facts,
assuming a causal connection among them.35But sometimes the observed effect can be attributed to several
causes and, therefore, having observed an effect we
cannot be sure about its cause. Fortunately, since
our beliefs that each possible cause could produce
that effect are not equal, the observation
modifies our beliefs on the different causes.
That is the essence of Bayesian reasoning.
Since `Bayesian' has several
flavors36
in the literature,
I summarize the points of view expressed here:
- Probability simply states, in a quantitative way,
how much we believe something. (If you like,
you can reason the other way around, thinking
that something is highly improbable if you
would be highly surprised if it occurs.37)
- ``Since the knowledge may be different with different persons or with
the same person at different times, they may anticipate the same event
with more or less confidence, and thus different numerical probabilities
may be attached to the same event.'' [11]
This is the subjective nature of probability.
- Initial probabilities can be elicited, with all the vagueness
of the case,38
on a pure subjective base (see Appendix C).
Virtual bets or comparisons with
reference events can be useful `tools' to
force ourselves or experts to provide quantitative
statements of our/their
beliefs. (See also Appendix C.)
- Probabilities can (but need not) be evaluated by past frequencies and
can even be expressed in terms of expected
frequencies of `successes' in hypothetical trials.
(See Appendix B.)
- Probabilities of causes are not generated, but only
updated by new pieces of evidence.
- Evidence is not only the `bare fact', but also all available
information about it (see Appendix D). This point is
often overlooked, as in the criticisms to Columbo's episode
raised by New Scientist [1].
- The update depends on how differently we believe that
the various
causes might produce the same effect (see also Appendix G).
- The probability of a single hypothesis cannot be
updated, if there isn't at least a second hypothesis
to compare with, unless the hypothesis is absolutely
incompatible with the effect [
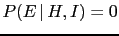 , and not
`as little', for example,
, and not
`as little', for example, 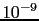 or
or 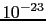 ].
Only in this special case an hypothesis is
definitely falsified. (See Appendix G.)
].
Only in this special case an hypothesis is
definitely falsified. (See Appendix G.)
- In particular, if there is only one hypothesis
in the game, the final probability of this hypothesis
will be one, no matter if it could produce the effect
with very small probability (but not zero).
39
- Initial probabilities depend on the information
stored somehow in our brain; being, fortunately,
each brain different from all others, it
is quite natural to admit that, in lack of
`experimental data',``quot capita, tot sententiae''.
(See Appendix C.)
- In the probabilistic inference (i.e. that stems from
probability theory) the updating rule is univocally
defined by Bayes' theorem (hence the adjective `Bayesian'
related to these methods).
- This objective updating rule makes final beliefs virtually
independent from the initial ones, if rational people
all share the same `solid' experimental information and
are ready to change their opinion (the latter
disposition has been named Cromwell's rule
by Dennis Lindley [18]).
- In the simple case that two hypotheses are involved,
the most convenient way to express the Bayes' rule is
final odds

Bayes factor
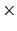
initial odds
- In some cases - almost always in scientific applications -
Bayes factors can be calculated exactly, or almost exactly,
in the sense that all experts will agree.
In many other real life cases their interpretation
as `virtual' odds (in the sense stated above) allows to
elicit them with the bet mechanism as any
subjective probability. (See Appendix C.)
- Bayes factors due to several independent pieces of evidence
factorize.
- The multiplicative updating rule can be turned into
an additive one using logarithms of the factors.
(See Appendix E.)
- The base 10 logarithms has been preferred here because
they are easily related to the orders of magnitudes of the odds
and the name `judgement leanings' (JL) has been chosen to have no
conflict with other terms already engaged in probability and statistics.
- Each logarithmic addend has the meaning of weight of evidence,
if the initial odds are taken as 0-th evidence.
- Individual contribution to the judgement
might be small in module and even
somehow uncertain, but, nevertheless, their combination
might result into strong convincingness. (See Appendix G.)
- In most real life cases there are not just
two alternative causes and two possible effects.
Moreover, causes can be effects of other causes and effects
can be themselves causes of other effects.
All hypotheses in the game make up a complex `belief network'.
Experts can certainly provide kinds of educated guesses
to state how likely a cause can generate several effects,
but the analysis of the full network goes well
beyond human capabilities, as discussed more extensively in
Appendix C and J.
- A next to simply case is when the evidence is mediated
by a testimony. The formal treatment in Appendix I
shows that, although experts can easily assess
the required ingredients, the conclusions are really
not so obvious.
- The question of the critical value of the
judgement leaning, above which a suspected
can be condemned, goes beyond the purpose of this notes,
focused on belief. That is a delicate decision problem that
inherits all issues of assessing beliefs, to which
the evaluations of benefits and losses need to be added.
And Galesco? Come on, there is little to argue.
 Nevertheless,
the reading of the instructive New Scientist article is
warmly recommended!
Nevertheless,
the reading of the instructive New Scientist article is
warmly recommended!![$ ]$](img259.png)
It is a pleasure to thank Pia and Maddalena, who
introduced me Columbo, and Dino Esposito,
Paolo Agnoli
and Stefania Scaglia for having taken part to
the post dinner jury that absolved him.
The text has benefitted
of the careful reading by Dino, Paolo and Enrico Franco
(see in particular his interesting remark in footnote 44).
Giulio D'Agostini
2010-09-30