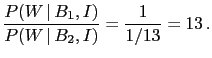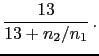Role of priors
Applying the updating reasoning to our box game,
the Bayes factor of interest is
As it was remarked, this number would give the required odds
if the hypotheses were initially equally likely.
But how strong are the initial relative beliefs
on the two hypotheses? `Unfortunately',
we cannot perform a probabilistic inversion
if we are unable to assign somehow prior probabilities to the
hypotheses we are interested in.9
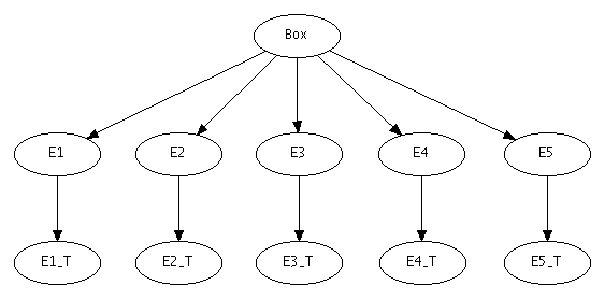
Figure:
Graphical representation of the causal connections
Box
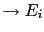 , where
, where 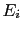 are the effects
(White/Black at each extraction). These effects are then causes
of other effects (
are the effects
(White/Black at each extraction). These effects are then causes
of other effects (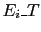 ), the reported colors, where `
), the reported colors, where `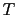 '
stands for `testimony'.
The arrows connecting the various `nodes' represent
conditional probabilities. The model will be fully exploited
in Appendix J.
'
stands for `testimony'.
The arrows connecting the various `nodes' represent
conditional probabilities. The model will be fully exploited
in Appendix J.
 |
Indeed, in the formulation of the problem I on purpose
passed over the relevant pieces of information
to evaluate the prior probabilities (it was said that
``there are two types of boxes'',
not ``there are two boxes''!). If we specify that
we had 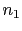 boxes of type
boxes of type 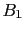 and
and 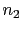 of the other kind,
then the initial odds
are
of the other kind,
then the initial odds
are 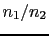 and the final ones will be
and the final ones will be
from which we get (just requiring that the probability of the two
hypotheses have to sum up to one10)
If the two hypotheses were initially considered equally likely,
then the evidence 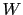 makes
makes 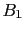 13 times more believable
than
13 times more believable
than 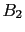 , i.e.
, i.e.
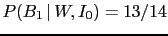 , or approximately 93%.
On the other hand, if
, or approximately 93%.
On the other hand, if 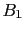 was a priori much less
credible than
was a priori much less
credible than 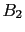 ,
for example by a factor 13,
just to play with round numbers, the same evidence
made
,
for example by a factor 13,
just to play with round numbers, the same evidence
made 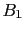 and
and 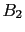 equally likely. Instead, if we were
initially in strong favor of
equally likely. Instead, if we were
initially in strong favor of 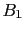 , considering it for instance
13 times more plausible than
, considering it for instance
13 times more plausible than 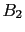 , that evidence
turned this factor into 169, making us 99.4% confident
- highly confident, some would even
say `practically sure'! -
that the box is of type
, that evidence
turned this factor into 169, making us 99.4% confident
- highly confident, some would even
say `practically sure'! -
that the box is of type 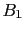 .
.
Giulio D'Agostini
2010-09-30