Next: Bayes theorem and Bayes Up: A defense of Columbo Previous: Introduction
Imagine there are two types of boxes, ![]() , that only contain
white balls (
, that only contain
white balls (![]() ), and
), and ![]() , that contain one
white balls and twelve black
(incidentally, just to be precise,
although the detail is absolutely irrelevant,
we have to infer from Columbo's words,
``You didn't touch any
of these twelve cameras. You picked up that one'',
the cameras were thirteen).
, that contain one
white balls and twelve black
(incidentally, just to be precise,
although the detail is absolutely irrelevant,
we have to infer from Columbo's words,
``You didn't touch any
of these twelve cameras. You picked up that one'',
the cameras were thirteen).
You take at random a box and extract a ball.
The resulting color is
white.
You might be interested to evaluate
the probability that the box is of type ![]() ,
in the sense of stating in a quantitative way
how much you believe
this hypothesis.
In formal terms we are interested in
,
in the sense of stating in a quantitative way
how much you believe
this hypothesis.
In formal terms we are interested in
![]() ,
knowing that
,
knowing that
![]() and
and
![]() , a problem that can be sketched as
, a problem that can be sketched as
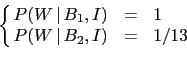 |
(1) |
A typical mistake
at this point is to
confuse
![]() with
with
![]() ,
or, more often,
,
or, more often,
![]() with
with
![]() ,
as largely discussed in Ref. [1].
Hence we need to learn how
to turn properly
,
as largely discussed in Ref. [1].
Hence we need to learn how
to turn properly
![]() into
into
![]() using the rules of probability
theory.
using the rules of probability
theory.