


Next: P-value based on the
Up: P-value analysis of the
Previous: P-value analysis of the
The expected number of events due to the null hypothesis
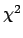 ``only background'' is 27.4 (
``only background'' is 27.4 (
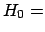 ).
Having observed 34 events we get:
).
Having observed 34 events we get:
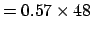 |
(1) |
a value that it is not considered `significative'. However, the obvious
criticism to this procedure is that we have only used the integrated number
of coincidences,
losing completely the detailed information provided by the time distribution.
The problem can be better understood in the limiting case of 1000 bins,
an expected background of 1 event/bin, and an experimental result in which 999 bins
have contents which `nicely' (Poisson) fluctuate around 1, and a single bin
exhibiting a spike of 31 counts. The p-value would be of 16%, accepting
the hypothesis that the data are explained well by background alone.
Giulio D'Agostini
2005-01-09