


Next: P-value based on the
Up: P-value analysis of the
Previous: P-value based on the
The naïve solution to this paradox is to calculate a p-value
using only the bin presenting the highest fluctuation. This approach would give
a very small number (
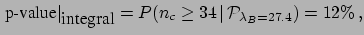 ) in our 1000 bin example, and would
remain below the
) in our 1000 bin example, and would
remain below the 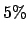 threshold even if the spike has only 5 events over
a background of 1.
Applying this reasoning to the ROG data we get
threshold even if the spike has only 5 events over
a background of 1.
Applying this reasoning to the ROG data we get
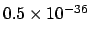 |
(2) |
a p-value which may be considered `significative'. (Note that, if we used the observed
background of Fig. 1, that we do not believe it is the correct number
to use, the p-value would be
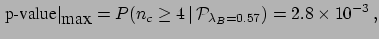 .)
.)
Giulio D'Agostini
2005-01-09