We need now to specify
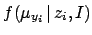 . As usual,
in lack of better knowledge, we take a Gaussian distribution
of unknown parameter
. As usual,
in lack of better knowledge, we take a Gaussian distribution
of unknown parameter 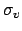 ,
with awareness that this is just a convenient, approximated
way to quantify our uncertainty.
,
with awareness that this is just a convenient, approximated
way to quantify our uncertainty.
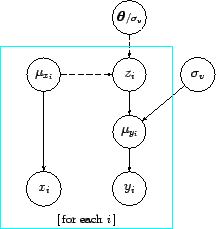
At this point a summary of all ingredients
of the model in the specific case of linear model is in order:
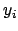 |
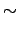 |
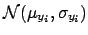 |
(39) |
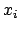 |
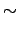 |
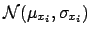 |
(40) |
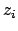 |
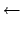 |
![$\displaystyle m\, \mu_{x_i} + c
\hspace{10.0mm} [\,\Rightarrow\ \delta(z_i- m\, \mu_{x_i} + c)\,]$](img146.png) |
(41) |
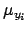 |
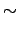 |
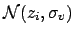 |
(42) |
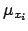 |
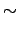 |
![$\displaystyle {\cal U}(-\infty,+\infty)
\hspace{5.0mm} [\,\Rightarrow\ k_{x_i}\,]$](img150.png) |
(43) |
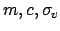 |
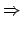 |
![$\displaystyle \mbox{see later} \hspace{12.4mm} [\,\Rightarrow \mbox{'uniform'}\,],$](img153.png) |
(44) |
where
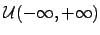 stands for a uniform distribution
over a very large interval, and the symbol `
stands for a uniform distribution
over a very large interval, and the symbol ` '
has been used to deterministically assign a value, as done in
BUGS[11] (see later).
'
has been used to deterministically assign a value, as done in
BUGS[11] (see later).
![$\displaystyle \prod_i
\frac{1}{\sqrt{\sigma^2_v + \sigma_{y_i}^2+m^2\,\sigma_{x...
...+ \sigma_{y_i}^2+m^2\,\sigma_{x_i}^2) }
\right]}\, f(m,c,\sigma_v\,\vert\,I)\,.$](img130.png)