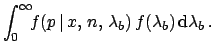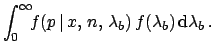Next: Poisson background on the
Up: Poisson background on the
Previous: Poisson background on the
In these examples we made the assumption that the expected number
of background events is well known. If this is not the case,
we can quantify our uncertainty about it by a pdf 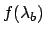 ,
whose modeling depends on our best knowledge about
,
whose modeling depends on our best knowledge about  .
Taking account of this uncertainty in a probabilistic approach
is rather simple, at least conceptually (calculations can
be quite complicate, but this is a different question).
In fact, applying probability theory we get:
.
Taking account of this uncertainty in a probabilistic approach
is rather simple, at least conceptually (calculations can
be quite complicate, but this is a different question).
In fact, applying probability theory we get:
We recognize in this formula that the pdf that takes
into account all possible values of 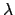 is a weighted average of all
is a weighted average of all 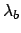 dependent pdf's,
with a weight equal to
dependent pdf's,
with a weight equal to 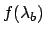 .
.
Giulio D'Agostini
2004-12-13