


Next: Correlation in results caused
Up: Uncertainties from systematic effects
Previous: Reweighting of conditional inferences
Joint inference and marginalization of
nuisance parameters
A different approach, which produces identical results,
is to think of a joint
inference about both the quantities of interest
and the influence variables:
Then, marginalization is applied to the variables that we are not
interested in (the so called nuisance parameters), obtaining
Equation (77) shows a peculiar feature of Bayesian inference,
namely the possibility making an inference about a number of
variables larger than the number of the observed data. Certainly,
there is no magic in it, and the resulting variables will be highly
correlated. Moreover, the prior cannot be improper in all
variables.
But, by using informative priors in which experts feel
confident,
this feature allows one to tackle complex problems with
missing or corrupted parameters. In the end, making use of
marginalization, one can concentrate on the quantities of real interest.
The formulation of the problem in terms of
Eqs. (77) and (79) allows one to
solve problems in which the influence variables might depend
on the true value 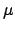 , because
, because
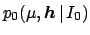 can model dependences between
can model dependences between 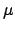 and
and
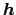 . In most
applications,
. In most
applications,
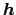 does not depend on
does not depend on 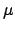 , and the
prior factors into the product of
, and the
prior factors into the product of
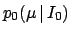 and
and
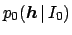 . When this happens,
we recover exactly the same results as obtained using
the reweighting of conditional inferences approach
described just above.
. When this happens,
we recover exactly the same results as obtained using
the reweighting of conditional inferences approach
described just above.



Next: Correlation in results caused
Up: Uncertainties from systematic effects
Previous: Reweighting of conditional inferences
Giulio D'Agostini
2003-05-13
![]() , because
, because
![]() can model dependences between
can model dependences between ![]() and
and
![]() . In most
applications,
. In most
applications,
![]() does not depend on
does not depend on ![]() , and the
prior factors into the product of
, and the
prior factors into the product of
![]() and
and
![]() . When this happens,
we recover exactly the same results as obtained using
the reweighting of conditional inferences approach
described just above.
. When this happens,
we recover exactly the same results as obtained using
the reweighting of conditional inferences approach
described just above.