


Next: Maximum-entropy priors
Up: General principle based priors
Previous: General principle based priors
Transformation invariance
An important class of priors arises from the requirement
of transformation invariance.
We shall consider two specific cases, translation invariance
and scale invariance.
- Translation invariance
-
Let us assume we are indifferent over a transformation
of the kind
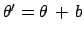 , where
, where 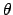 is our
variable of interest
and
is our
variable of interest
and 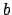 a constant.
Then
a constant.
Then
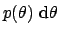 is an infinitesimal mass element of probability
for
is an infinitesimal mass element of probability
for 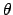 to be in the interval
to be in the interval
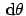 . Translation invariance
requires that this mass element remains unchanged when expressed
in terms of
. Translation invariance
requires that this mass element remains unchanged when expressed
in terms of 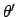 , i.e.
, i.e.
since
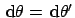 .
It is easy to see that in order for Eq. (101) to hold for any
.
It is easy to see that in order for Eq. (101) to hold for any 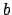 ,
,
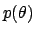 must be equal to a constant for all values of
must be equal to a constant for all values of
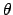 from
from 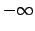 to
to 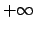 . It is therefore an improper prior.
As discussed above,
this is just a convenient modelling. For practical purposes this prior
should always be regarded as the limit for
. It is therefore an improper prior.
As discussed above,
this is just a convenient modelling. For practical purposes this prior
should always be regarded as the limit for
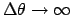 of
of
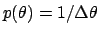 ,
where
,
where 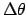 is a large finite range around the values of interest.
is a large finite range around the values of interest.
- Scale invariance
-
In other cases, we could be indifferent about a scale transformation,
that is
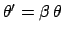 , where
, where 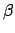 is a constant. This invariance
implies, since
is a constant. This invariance
implies, since
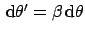 in this case,
in this case,
i.e.
The solution of this functional equation is
as can be easily proved using Eq. (104) as test solution in
Eq. (103).
This is the famous Jeffreys' prior, since it was first proposed
by Jeffreys. Note that this prior also can be stated as
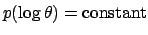 , as can be easily verified.
The requirement of scale invariance also
produces an improper prior, in the range
, as can be easily verified.
The requirement of scale invariance also
produces an improper prior, in the range
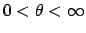 .
Again, the improper prior must be understood as the limit of a proper prior
extending several orders of magnitude around the values of interest.
[Note that we constrain
.
Again, the improper prior must be understood as the limit of a proper prior
extending several orders of magnitude around the values of interest.
[Note that we constrain 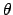 to be positive because, traditionally,
variables which are believed to satisfy this invariance are associated with
positively defined quantities. Indeed, Eq. (104)
has a symmetric solution for negative quantities.]
to be positive because, traditionally,
variables which are believed to satisfy this invariance are associated with
positively defined quantities. Indeed, Eq. (104)
has a symmetric solution for negative quantities.]
According to the supporters of these invariance motivated priors
(see e.g. Jaynes 1968, 1973, 1998, Sivia 1997, and Fröhner 2000,
Dose 2002) variables associated to translation invariance are
location parameters, as the parameter 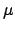 in a Gaussian model;
variables associated to scale invariance are scale parameters,
like
in a Gaussian model;
variables associated to scale invariance are scale parameters,
like 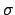 in a Gaussian model or
in a Gaussian model or 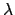 in a Poisson model.
For criticism about the (mis-)use of this kind
of prior see (D'Agostini 1999d).
in a Poisson model.
For criticism about the (mis-)use of this kind
of prior see (D'Agostini 1999d).



Next: Maximum-entropy priors
Up: General principle based priors
Previous: General principle based priors
Giulio D'Agostini
2003-05-13