


Next: Importance sampling
Up: Monte Carlo methods
Previous: Estimating expectations by sampling
Let us assume we are able to generate points according to
some function
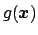 , such that, given a constant
, such that, given a constant 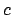 ,
,
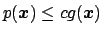 . We generate
. We generate
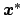 according to
according to
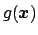 and decide to accept it with probability
and decide to accept it with probability
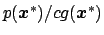 (i.e. we extract another random number between 0 and 1 and accept the point
if this number is below that ratio).
It is easy to show that this procedure reshapes
(i.e. we extract another random number between 0 and 1 and accept the point
if this number is below that ratio).
It is easy to show that this procedure reshapes
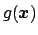 to
to
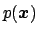 and that it does not depend on the absolute normalization
of
and that it does not depend on the absolute normalization
of
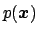 (any normalization constant can be absorbed in the multiplicative constant
(any normalization constant can be absorbed in the multiplicative constant 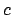 ).
A trivial choice of
).
A trivial choice of
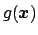 , especially for simple one-dimensional problems,
is a uniform distribution (this variation is known as the hit or miss method),
though clearly it can be very inefficient.
, especially for simple one-dimensional problems,
is a uniform distribution (this variation is known as the hit or miss method),
though clearly it can be very inefficient.
Giulio D'Agostini
2003-05-13