The function
![]() can be used
in the calculation of
can be used
in the calculation of
![]() , if we
notice that
, if we
notice that
![]() can be rewritten as follows:
can be rewritten as follows:
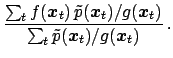 |
(115) |
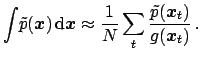 |
(116) |
It easily to see that the method works well if
![]() overlaps well
with
overlaps well
with
![]() . Thus, a proper choice of
. Thus, a proper choice of
![]() can be made
by studying where the probability mass of
can be made
by studying where the probability mass of
![]() is concentrated
(for example finding the mode of the distribution in a numerical way).
Often a Gaussian function is used for
is concentrated
(for example finding the mode of the distribution in a numerical way).
Often a Gaussian function is used for
![]() , with parameters
chosen to approximate
, with parameters
chosen to approximate
![]() in the proximity of the mode,
as described in Sect. 5.10. In other cases, other functions
can be used which have more pronounced tails, like
in the proximity of the mode,
as described in Sect. 5.10. In other cases, other functions
can be used which have more pronounced tails, like ![]() -Student
or Cauchy distributions. Special techniques, into which we cannot enter here,
allow
-Student
or Cauchy distributions. Special techniques, into which we cannot enter here,
allow ![]() independent random numbers to be generated and, subsequently,
by proper rotations, turned into other numbers which have a correlation matrix
equal to that of the multi-dimensional
Gaussian which approximates
independent random numbers to be generated and, subsequently,
by proper rotations, turned into other numbers which have a correlation matrix
equal to that of the multi-dimensional
Gaussian which approximates
![]() .
.
Note, finally, that, contrary to the rejection sampling, importance sampling is not suitable for generate samples of `unweighted events', such as those routinely used in the planning and the analysis of many kind experiments, especially particle physics experiments.