| (117) |
- if
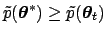 , then accept
, then accept
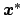 ;
;
- if
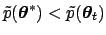 , extract a uniform random
number between 0 and 1 and accept
, extract a uniform random
number between 0 and 1 and accept
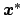 if
the random number is less then
if
the random number is less then
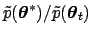 .
.
| (117) |
| (118) |
The fact that this algorithm belongs to the class of MCMC gives rise to two problems. First, each point in the chain has some correlation with the points which immediately preceded it, and usually the chain moves slowly (and irregularly) from one region in the variable space to another (note also that, if a proposed point is not accepted, the chain keep the same position in the next step, and this circumstance can happen several times consecutively). Second, the initial part of the sequence is strongly influenced by the arbitrary starting point. Therefore, it is necessary to remove the initial part of the chain.
Using an MCMC for a complex problem is not an automatic procedure and some tuning is needed. One of the important things to choose with care is the proposal function. If too small jumps are proposed, the chain moves too slowly and, can even remain trapped in a subregion and never sample the rest of the parameter space, if the probability distribution is defined over disconnected regions. If too large steps are proposed, the proposed points could often fall in very low probability regions and not be accepted, in which case the chain remains stuck in a point for many cycles.
For an interesting, insightful introduction to principles and applications of MCMC see (Kass et al 1998). A nice tutorial is given by (Hanson 2000). A recent application of Bayesian methods in cosmology, which uses MCMC and contains a pedagogical introduction too, can be found in (Lewis and Bridle 2002). For a good treatise, freely available on the web, (Neel 1993) is recommended. The reader will find that MCMC techniques are used to solve complex problems graphically represented in terms of Bayesian networks (also known as belief networks or simply probabilistic network). This subject, which has revolutionized the way of thinking artificial intelligence and the uncertainty issues related to it, does beyond the purpose of this article. The interested reader can find more information in (Pearl 1988, BUGS 1996, Cowell et al 1999 and Cozman 2001) and references therein.