


Next: Forward to the past:
Up: From Observations to Hypotheses
Previous: Inference, forecasting and related
Falsificationism and its statistical variations
The essence of the so called falsificationism
is that a theory should yield verifiable predictions,
i.e. predictions that can be checked
to be true or false. If an effect is observed
that contradicts the theory, the theory is ruled out, i. consistently. it is
falsified.
Though this scheme is
certainly appealing, and most scientists are convinced that this
is the way Science proceeds,2 it is easy to
realize that this scheme
is a bit naïve, when one tries to apply it literally,
as we shall see in a while. Before doing that,
it is important
to recognize that falsificationism is nothing but an
extension of the classical proof by contradiction
to the experimental method.
The proof by contradiction of standard dialectics and mathematics
consists in assuming true a hypothesis and in looking
for (at least) one of its logical consequences
that is manifestly false.
If a false consequence exists,
then the hypothesis under test is considered false
and its opposite true (in the sequel 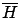 will indicate
the hypothesis opposite to
will indicate
the hypothesis opposite to 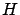 , i.e.
, i.e. 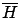 is
true if
is
true if 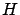 false, and vice versa).
Indeed, there is no doubt that if we observe an effect that
is impossible within a theory, this theory
has to be ruled out. But the strict application of the
falsificationist criterion is not maintainable in the
scientific practice for several reasons.
false, and vice versa).
Indeed, there is no doubt that if we observe an effect that
is impossible within a theory, this theory
has to be ruled out. But the strict application of the
falsificationist criterion is not maintainable in the
scientific practice for several reasons.
- What should we do of all theories which have not been falsified yet?
Should we consider them all at the same level, parked
in a kind of Limbo? This approach is not very
effective. Which experiment should we perform next? The natural
development of Science shows that new investigations are made
in the direction that seems mostly credible
(and fruitful) at a given moment.
- If the predictions of a theory are characterized by the
internal or external probabilistic behavior discussed above,
how can we ever think of
falsifying such a theory, speaking rigorously?
For instance, there is no way to falsify hypothesis
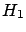 of Example 1, because any real number is compatible
with any Gaussian.
For the same reason, falsificationism cannot be used to make
an inference about the value of a physical quantity
(for a Gaussian response of the detector,
no value of
of Example 1, because any real number is compatible
with any Gaussian.
For the same reason, falsificationism cannot be used to make
an inference about the value of a physical quantity
(for a Gaussian response of the detector,
no value of 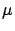 can be falsified whatever we observe,
and, unfortunately,
falsificationism does not tell how to classify non-falsified values
in credibility).
can be falsified whatever we observe,
and, unfortunately,
falsificationism does not tell how to classify non-falsified values
in credibility).
An extension of strict falsificationism
is offered by the
statistical test methods developed by statisticians.
Indeed, the latter methods might be seen as attempts of
implementing in practice the falsificationism principle.
It is therefore important to understand the `little' variations of
the statistical
tests with respect to the proof of contradiction
(and hence to strict falsificationism).
- a)
- The impossible consequence is replaced by an
improbable consequence.
If this improbable consequence
occurs, then the hypothesis is rejected, otherwise it is accepted.
The implicit argument on the basis of the
hypothesis test approach of
conventional statistics
is: ``if
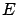 is practically impossible given
is practically impossible given 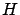 ,
then
,
then 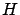 is considered practically false given
the observation
is considered practically false given
the observation 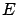 .''
But this probability inversion -- initially qualitative,
but then turned erroneously quantitative by most practitioners,
attributing to `
.''
But this probability inversion -- initially qualitative,
but then turned erroneously quantitative by most practitioners,
attributing to `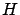 given
given 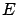 ' the
same probability of `
' the
same probability of `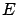 given
given 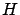 ' -- is not logically
justified and it is not difficult to show that it
yields misleading conclusions.
Let us see some simple examples.
' -- is not logically
justified and it is not difficult to show that it
yields misleading conclusions.
Let us see some simple examples.
- Example 2
- Considering only hypothesis
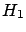 of Example 1
and taking
of Example 1
and taking 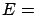 ``
``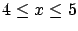 '', we can
calculate the probability of obtaining
'', we can
calculate the probability of obtaining 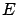 from
from 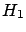 :
:
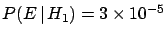 . This probability is rather small, but,
once
. This probability is rather small, but,
once 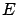 has occurred, we cannot state that
``
has occurred, we cannot state that
``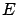 has little probability to come from
has little probability to come from 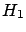 '', or that
``
'', or that
``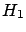 has little probability to have caused
has little probability to have caused 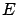 '':
'':
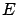 is certainly due to
is certainly due to 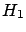 !
!
- Example 3
- ``I play honestly at lotto, betting on a rare combination'' (
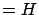 )
and ``win'' (
)
and ``win'' (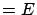 ). You cannot say that since
). You cannot say that since 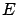 is
`practically impossible' given
is
`practically impossible' given 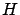 ,
then hypothesis
,
then hypothesis 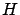 has to be `practically excluded', after you have got
the information that I have won [such a conclusion would imply that
it is `practically true' that ``I have cheated'' (
has to be `practically excluded', after you have got
the information that I have won [such a conclusion would imply that
it is `practically true' that ``I have cheated'' (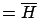 )].
)].
- Example 4
- An AIDS test to detect HIV infection is perfect to tag
HIV infected people as `positive' (=Pos),
i.e.
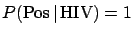 , but it can sometimes err, and
classify healthy persons
(
, but it can sometimes err, and
classify healthy persons
(
 ) as positive,
although with low probability, e.g.
) as positive,
although with low probability, e.g.
 .
An Italian citizen is chosen
at random to undergo such a test and he/she is tagged positive.
We cannot claim that ``since it was practically impossible that a
healthy person resulted positive, then this person is practically
infected'', or, quantitatively,
``there is only 0.2% probability that this
person is not infected''.
.
An Italian citizen is chosen
at random to undergo such a test and he/she is tagged positive.
We cannot claim that ``since it was practically impossible that a
healthy person resulted positive, then this person is practically
infected'', or, quantitatively,
``there is only 0.2% probability that this
person is not infected''.
We shall see later how to solve these kind of problems correctly.
For the moment the important message is that it is not
correct to replace `improbable' in logical methods that
speak about `impossible' (and to use then the reasoning
to perform `probabilistic inversions'): impossible and improbable differ
in quality, not just in quantity!
- b)
- In many cases the number of effects due to a hypothesis is so large
that each effect is `practically
impossible'.3
Even those who trust the reasoning based on the
small probability of effects to falsify hypotheses
have to realize that the reasoning fails in these cases,
because every observation
can be used as an evidence against the hypothesis
to be tested.
Statisticians have then
worked out methods in which
the observed effect
is replaced by two ensembles of effects,
one of high chance and another of low chance.
The reasoning based on the `practically impossible' effect
is then extended to
the latter ensemble.
This is the essence of all tests
tests based on ``p-values''[8]
(what physicists know as ``probability
of tails'' upon which 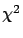 and other famous tests are based).
Logically,4 the situation gets worse, because
conclusions do not depend anymore on what has been
observed,
but also
on effects that have not been observed5(see e.g. Ref. [7]).
and other famous tests are based).
Logically,4 the situation gets worse, because
conclusions do not depend anymore on what has been
observed,
but also
on effects that have not been observed5(see e.g. Ref. [7]).
- c)
- Apart from the simple case of just one observation,
the data are summarized by a `test variable' (e.g.
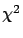 ),
function of the data,
and the reasoning discussed above is applied
to the test variable.
This introduces an additional, arbitrary ingredient
to this already logically tottering
construction.6
),
function of the data,
and the reasoning discussed above is applied
to the test variable.
This introduces an additional, arbitrary ingredient
to this already logically tottering
construction.6
- d)
- Even in simple problems, that could be formulated in
terms of a single quantity,
given the empirical information
there might be ambiguity
about which quantity plays the role of the random variable upon which
the p-value has to be
calculated.7
Anyhow, apart from questions that might seem subtle philosophical
quibbles, conventional tests lead to several practical problems.
- In my opinion the most serious problem is the fact that p-values
are constantly used in scientific conclusions
as if they were the probability that the hypothesis
under test is true (for example people report a p-value of 0.0003
as ``the hypothesis is excluded at 99.97% C.L.'', as if they were
99.97% confident that the hypothesis to test is false).
The consequence of this misunderstanding is very serious, and it is
essentially responsible for all claims of fake discoveries
in the past decades
(see some examples in Sec. 1.9 of Ref. [1].)
- Statistical tests are not based on first principles of any kind.
Hundreds of statistical tests have been contrived and their choice
is basically arbitrary. I have experienced that
discussions in experimental teams about which
test to use and how to use it are not deeper than discussions
in pubs among soccer fans (Italian readers might think at the
`Processo di Biscardi' talk show, quite often also in the tones).
- There is sometimes a tendency to look for the test that
gives the desired result. Personally, I find that
the fancier
the name of the test is, the less believable the claim is,
because I am pretty sure that other,
more common tests were discarded
because `they were not appropriate', an expression to be
often interpreted
as ``the other tests did not support what
the experimentalist
wanted the data to
prove''
(and I could report of people
that, frustrated by the `bad results' obtained with frequentistic tests,
contacted me hoping for a Bayesian miracle --
they got regularly
disappointed because, `unfortunately',
Bayesian methods, consciously applied,
tend not to feed vain illusions).
- Standard statistical methods, essentially a contradictory collection of
ad-hoc-eries, induce scientists, and physicists in particular,
to think that `statistics' is something `not serious',
thus encouraging
`creative' behaviors.8



Next: Forward to the past:
Up: From Observations to Hypotheses
Previous: Inference, forecasting and related
Giulio D'Agostini
2004-12-22
![]() will indicate
the hypothesis opposite to
will indicate
the hypothesis opposite to ![]() , i.e.
, i.e. ![]() is
true if
is
true if ![]() false, and vice versa).
Indeed, there is no doubt that if we observe an effect that
is impossible within a theory, this theory
has to be ruled out. But the strict application of the
falsificationist criterion is not maintainable in the
scientific practice for several reasons.
false, and vice versa).
Indeed, there is no doubt that if we observe an effect that
is impossible within a theory, this theory
has to be ruled out. But the strict application of the
falsificationist criterion is not maintainable in the
scientific practice for several reasons.