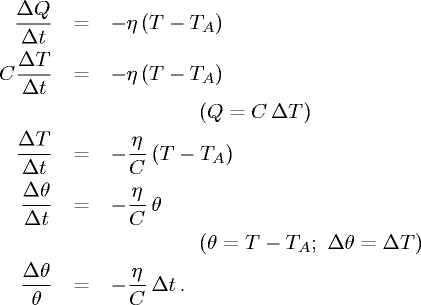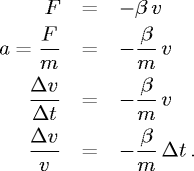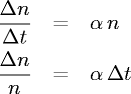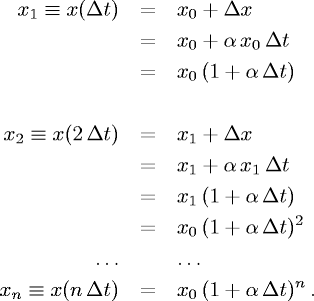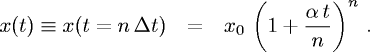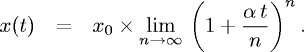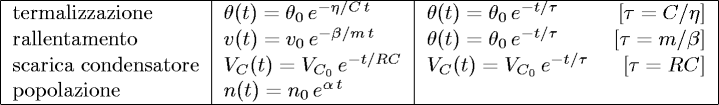Nota sugli esponenziali
- Ricordiamo innanzitutto dei problemi che abbiamo già incontrato
- Termalizzazione: il calore scambiato nell'unità di tempo è proporzionale
alla differenza di temperatura,
con un coefficiente che dipende dalle proprietà
fisiche e geometriche della superficie di contatto.
Chiamando t il tempo,
T la temperatura istantanea del corpo,
TA la temperatura ambiente,
θ la differenza fra T e
TA,
Q la quantità di calore,
C la capacità termica
(legata al calore specifico c dalla
relazione C = c m, ove m è la massa del corpo)
e η un coefficiente da cui dipende la dispersione termica, abbiamo:
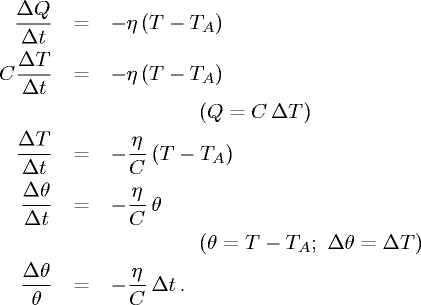
- Corpo frenato da attrito di viscosità proporzionale alla velocità
con coefficiente di proporzionalità β.
Con i soliti simboli per
forza, massa e velocità otteniamo:
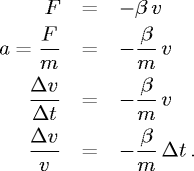
- Scarica di un condensatore di capacità C su una resistenza R.
→ lezioni precedenti
- Problemi aventi la stessa struttura matematica:
- Aumento/decremento di popolazione
(assumendo tasso di crescita/decrescita costante):
l'incremento di popolazione n nell'unità di tempo è
proporzionale al numero
di individui
della popolazione e da una costante ('α'):
- positiva se le nascite supera il numero di morti;
- negativa nel caso contrario;
- nullo nel caso di 'crescita zero').
Si ottiene quindi
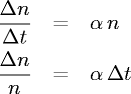
- Aumento di capitale,
dato un tasso di interesse i nel tempo unitario:
→ analogo
a crescita di popolazione, con α solo positiva.
- Decadimento di nuclei radioattivi:
→ analogo
a crescita di popolazione, con α solo negativa.
↠ Tutti questi problemi hanno la stessa struttura formale,
data la generica variabile x

→ la variazione relativa ('percentuale') della variabile è
proporzionale all'intervallo di tempo.
Possiamo riscrivere la stessa equazione come
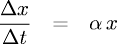
→ il tasso di crescita/decrescita (a seconda del segno di α) di una variabile è
proporzionale al valore della variabile.
↠ Si tratta ora di capire come varia x con il tempo.
- Cominciamo a vedere cosa succede
dopo Δt, dopo 2Δt, etc., partendo dal valore x0 all'istante t=0:
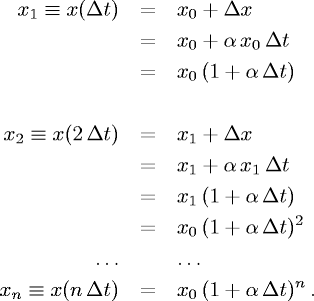
- Si tratta quindi di una progressione geometrica
di ragione (1+αΔt),
maggiore o minore di 1 a seconda del segno di α.
Dopo un tempo t = nΔt si ha quindi
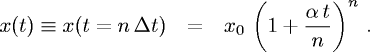
- Immaginiamo di 'affettare' ora il tempo t in tantissimi intervallini Δt.
Al limite, il numero di intervallini diventa 'infinito' e la loro ampiezza 'nulla'.
Si tratta di trovare quindi il limite
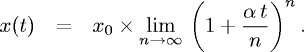
- Cerchiamo di capire quanto vale questo limite in modo 'pratico', non rigoroso,
analizzando
la seguente tabella compilata con αt=1 e αt=-1.
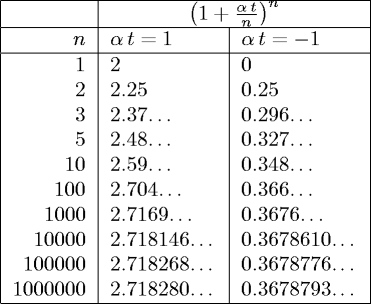
- Come si può verificare facilmente, il limite converge a
eαt,
ove e è la costante di Eulero, base dei logaritmi naturali
(in effetti, vedi bibliografie, una delle definizioni di e è proprio
legata a questo limite.
- In conclusione, la soluzione cercata è
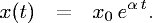
- Finalmente, sostituendo ad α i parametri dei diversi problemi, abbiamo
le diverse soluzioni:
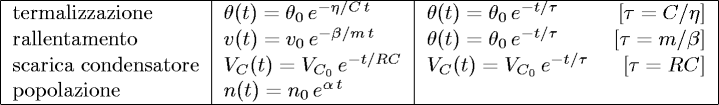
Nella tabella abbiamo indicato, ove ha interesse,
con τ la costante di tempo del processo,
un parametro che ci indica, in qualche modo, la velocità del processo:
- minore è τ, più rapido è il processo.
In particolare, si noti come, nel caso di esponenziali negativi
(i primi tre casi),
per t=τ la grandezza in esame di riduce di 1/e rispetto
al valore iniziale,
ovvero di circa il 37% (si ricorda come θ rappresenta la
differenza di temperatura rispetto all'ambiente).
[Problemino: → nel caso della termalizzazione e del rallentamento
si cerchi di dare una giustificazione intuitiva
delle dipendenze delle costanti di tempo dai parametri del problema.]
Altro esempio didatticamente interessante di crescita esponenziale:
- tacchino esponenziale:
mangia proporzionalmente al suo peso e aumenta di peso esattamente
di quanto mangia.
Bibliografia
- Costante e di Eulero: vedi
qui
o qui
(il secondo link soprattutto per l'equivalenza >
fra le due definizioni più note).
Torna indietro
— Home