Fisica per il CdS in SMIA
Prof. G. D'Agostini
A.A. 24-25


| ------------- | ------------- | 1. Gio 27/02 |
| 2. Lun 3/03 | 3. Mar 4/03 | 4. Gio 6/03 |
| 5. Lun 10/03 | 6. Mar 11/03 | 7. Gio 13/03 |
| 8. Lun 17/03 | 9. Mar 18/03 | 10. Gio 20/03 |
| 11. Lun 24/03 | 12. Mar 25/03 | 13. Gio 27/03 |
| 14. Lun 31/03 | 15. Mar 1/04 | 16. Gio 3/04 |
| 17. Lun 7/04 | 18. Mar 8/04 | 19. Gio 10/04 |
| 20. Lun 14/04 | 21. Mar 15/04 | ------------- |
| ------------- | ------------- | ------------- |
| 22. Lun 28/04 | 23. Mar 29/04 | ------------- |
| 24. Lun 5/05 | 25. Mar 6/05 | 26. Gio 8/05 |
| 27. Lun 12/05 | 28. Mar 13/05 | 29. Gio 15/05 |
| 30. Lun 19/05 | 31. Mar 20/05 | 32. Gio 22/05 |
| 33. Lun 26/05 | |
34. Gio 29/05 |
| ------------- | 35. Mar 3/06 Aula Picone |
36. Gio 5/06 |
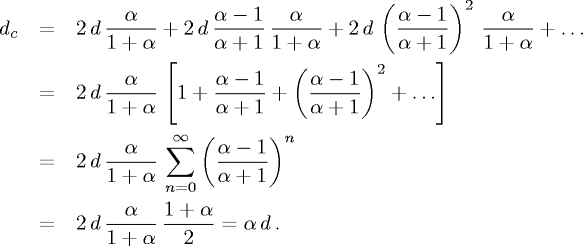
|
Ma cosa'è l'energia?
(Box fuori programma per chi volesse approfondire) → Concetto legato alla sua conservazione — Definizione in Wikipedia inglese (si stressa la sua proprietà di esser traferita senza scomparire) — Definizione in Wikipedia italiana (legata alla "capacità di compiere lavoro":(*) → uhm... pessima) — [idem su Treccani e libri di testi,(**) almeno per quanto riguarda la definizione] — Un articolo abbastanza recente sulla questione (più o meno ok) — Interessante la voce di Wikipedia francese e la citazione di Max Plank riportata — in fondo alla parte storica (e l'articolo richiamato nella nota 48 — sito visitato 10/04/2024): — "Tratterò del concetto di energia solo nella misura in cui può essere attaccato al principio — che dà il titolo a questo saggio, supponendo che il concetto di energia in fisica — tragga il suo significato soprattutto dal principio di conservazione che la riguarda" [→ Feynman] —(Das Prinzip der Erhaltung der Energie, 1887) — Interessanti slides sul tema (Bevilacqua, Falomo, Falabretti) — Un classico sul tema è History and Root of the Principle of the Conservation of Energy — di Ernst Mach: versione inglese scaricabile da questo link (vedi anche qui). — (Fra l'altro Mach è già stato citato durante il corso perché ringraziato, — insieme a David Hume, da Einstein, per averlo 'incoraggiato' a portare avanti — le sue idee rivoluzionarie.) |
(*) Uhm...
(**) Diciamo 'furbescamente', ma senza dire niente di errato.
|

[(*) Per chi fosse interessato
(ovviamente fuori programma):
(schematizzata qui, da Bayesian reasoning in data analysis) Si notino, in tale derivazione:
mentre nel successivo 'paragrafo' 179 propone l'uso dei minimi quadrati per trovare il valore più probabile delle grandezze fisiche incognite) |
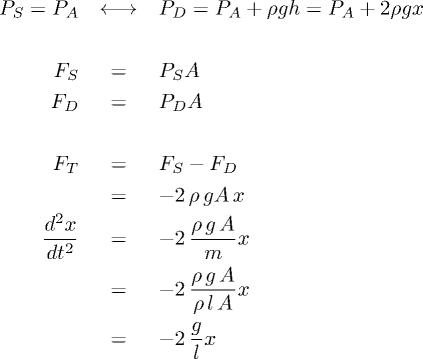

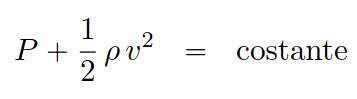
 Esami: possibili date
prova scritta esssione estiva.
Esami: possibili date
prova scritta esssione estiva.