Fisica per SMIA (2024/2025)
(G. D'Agostini)






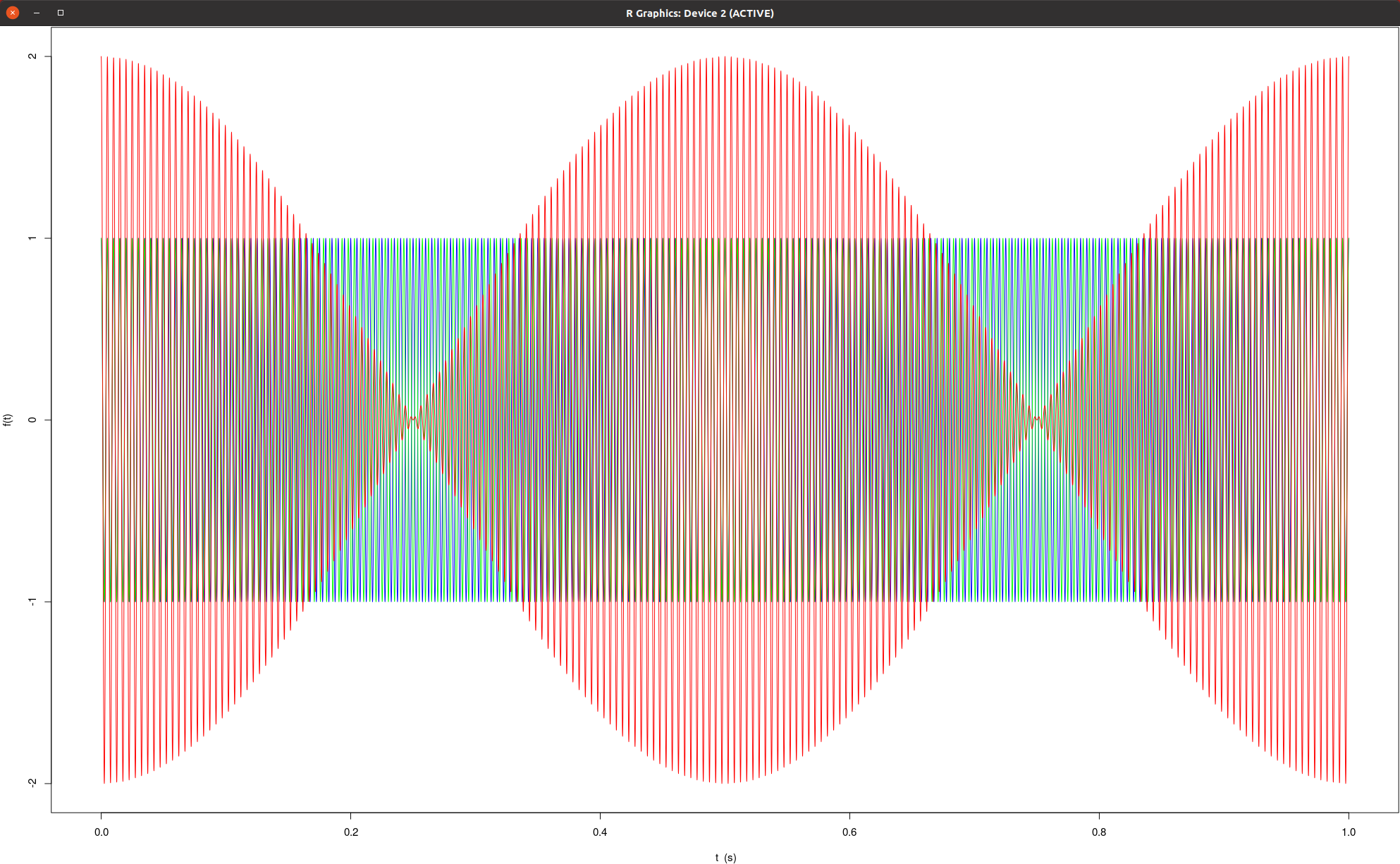
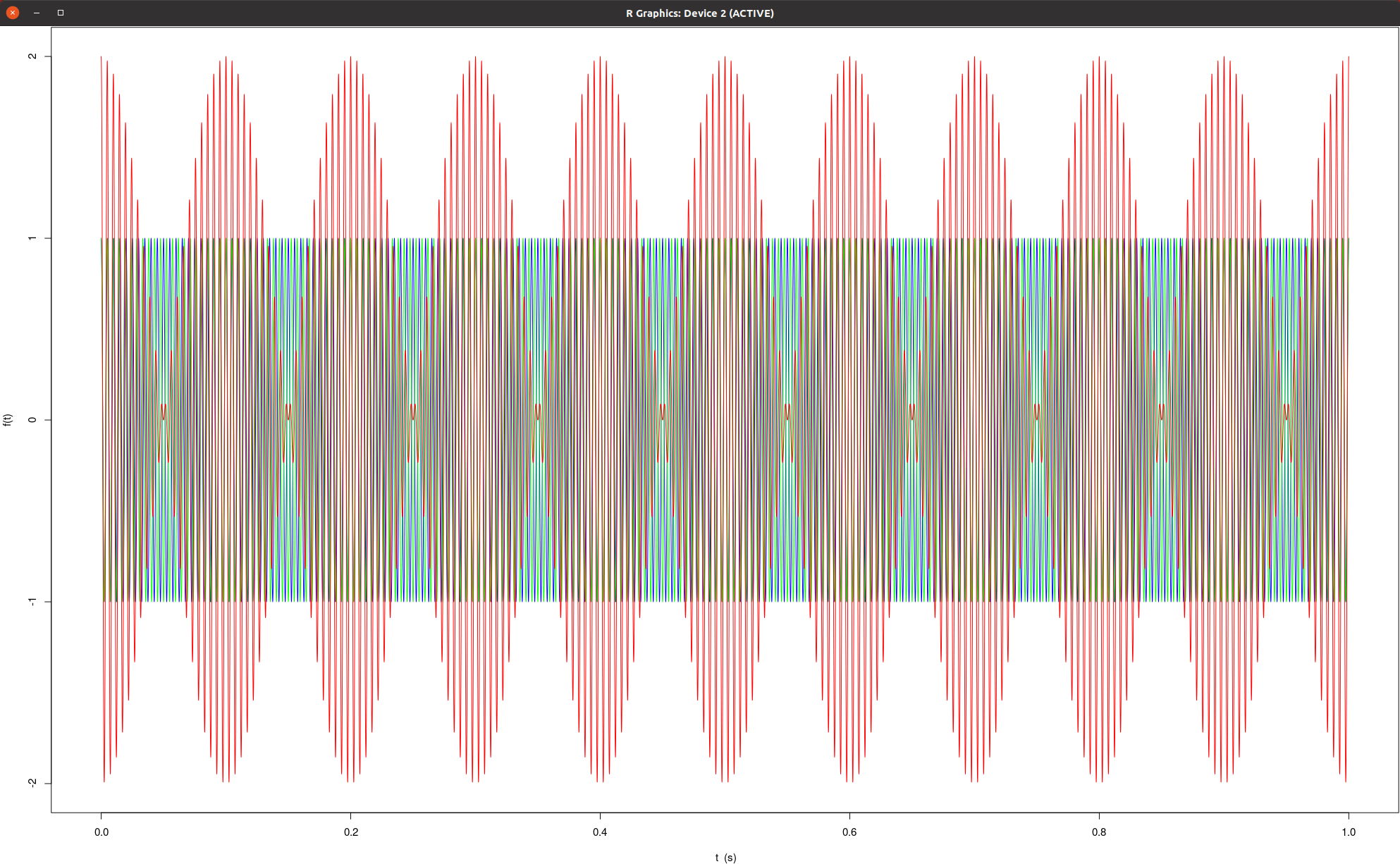
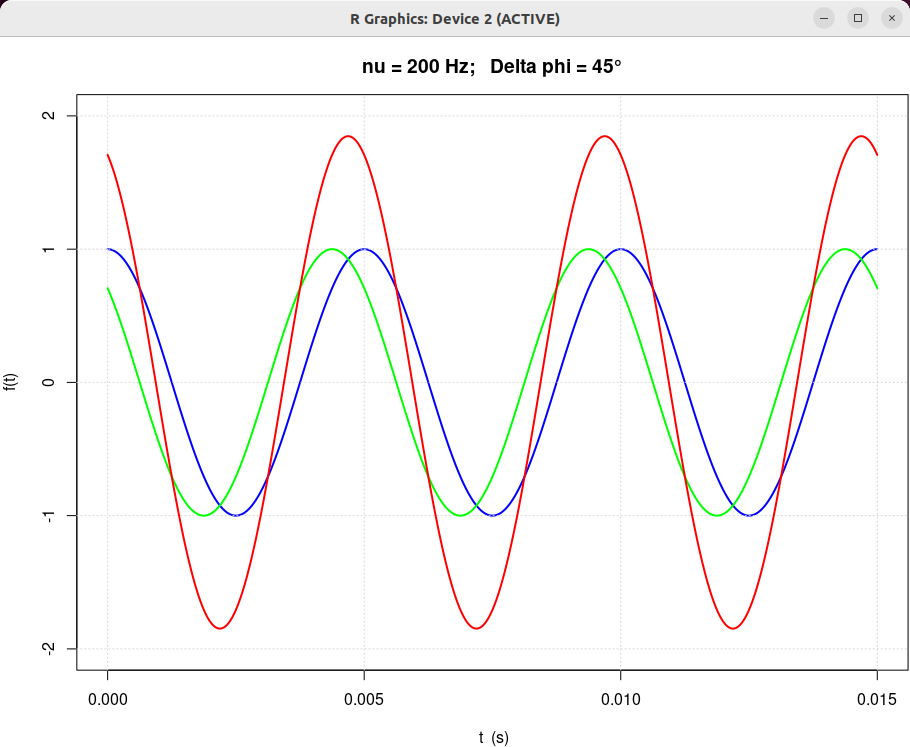





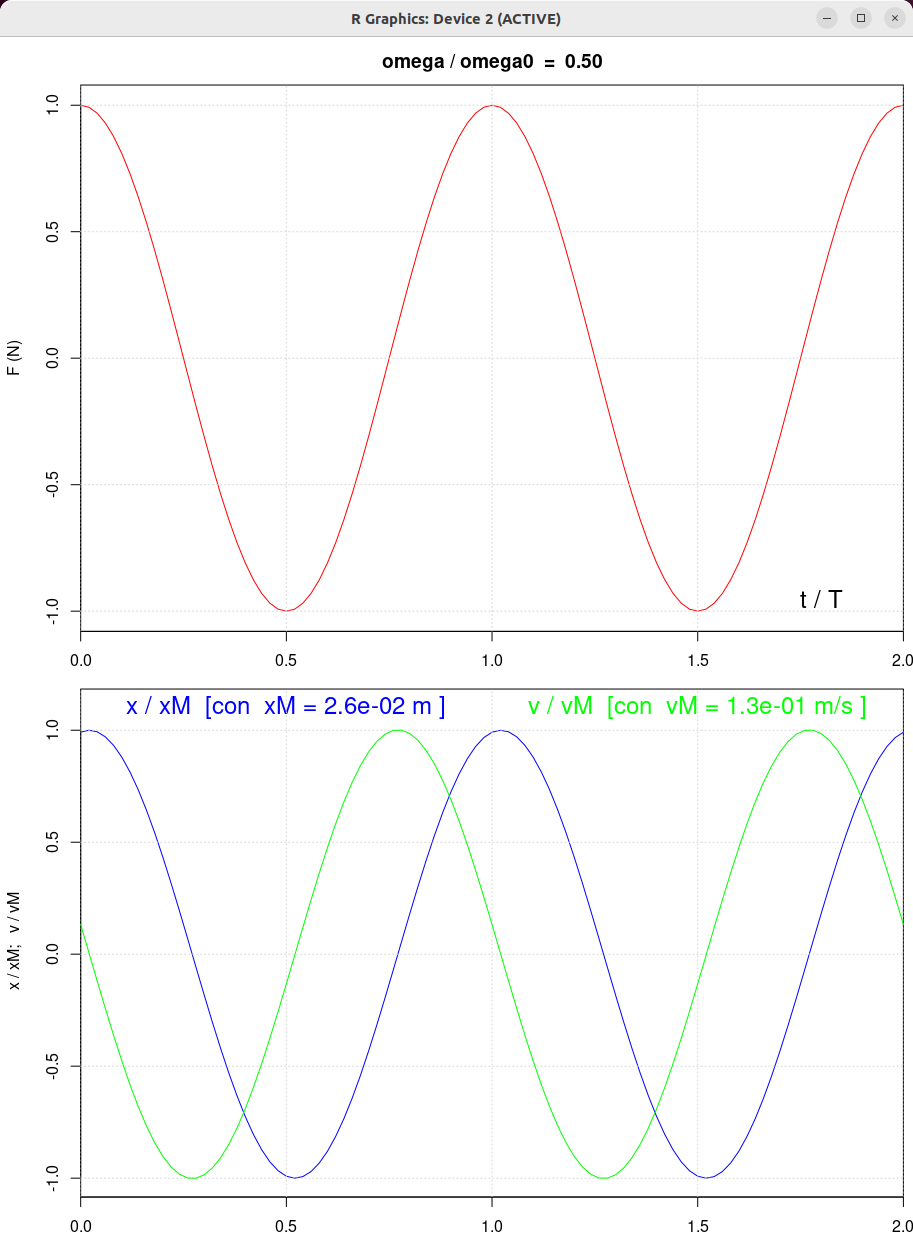
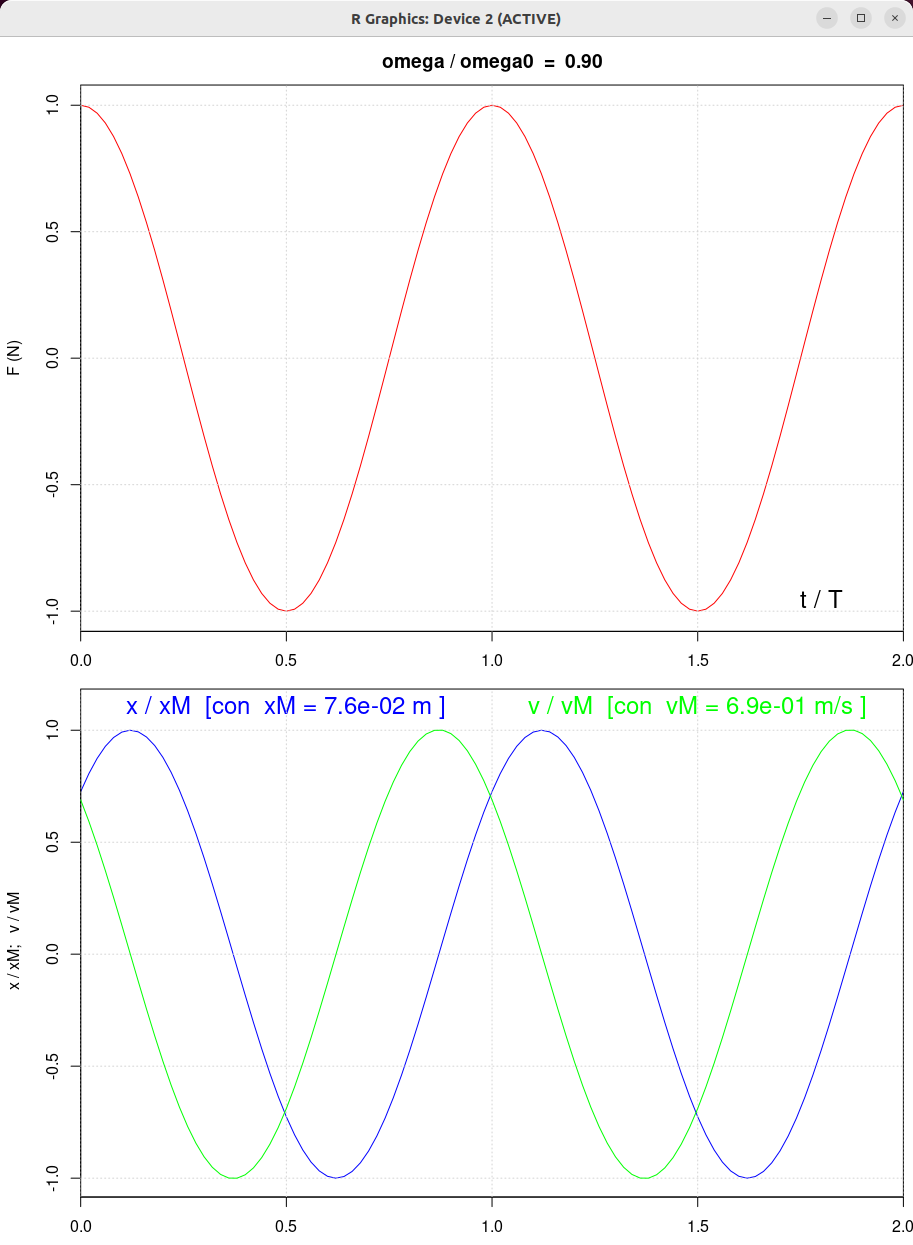
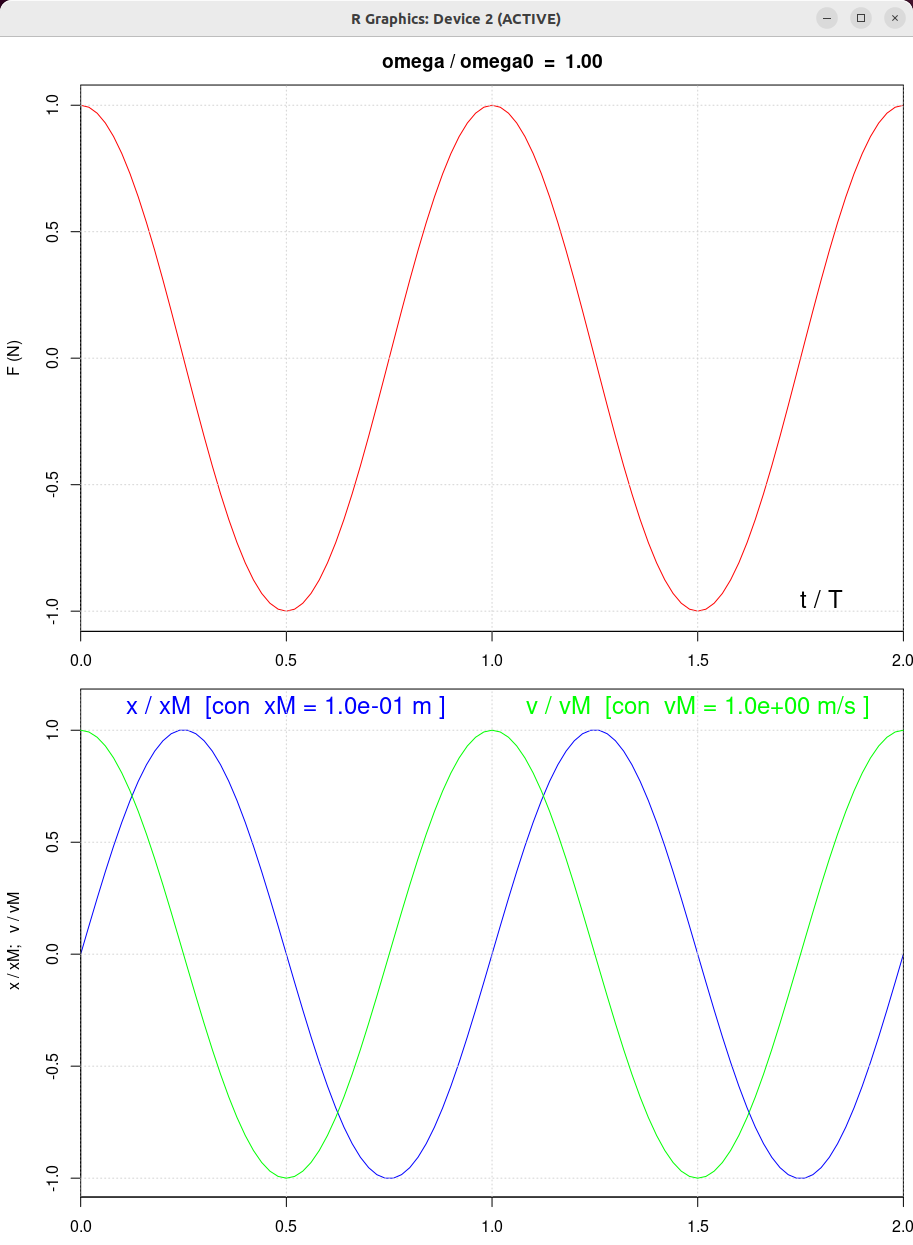
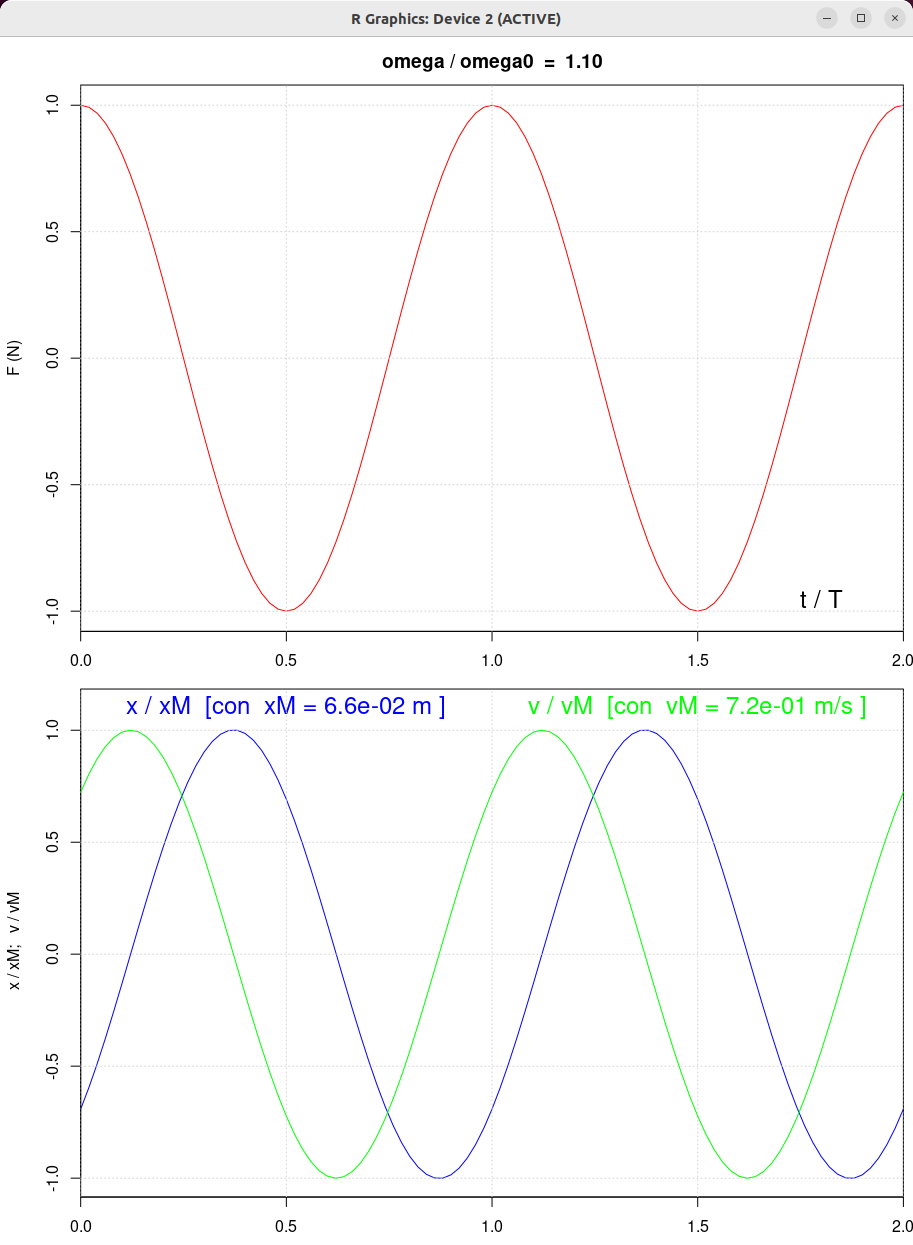
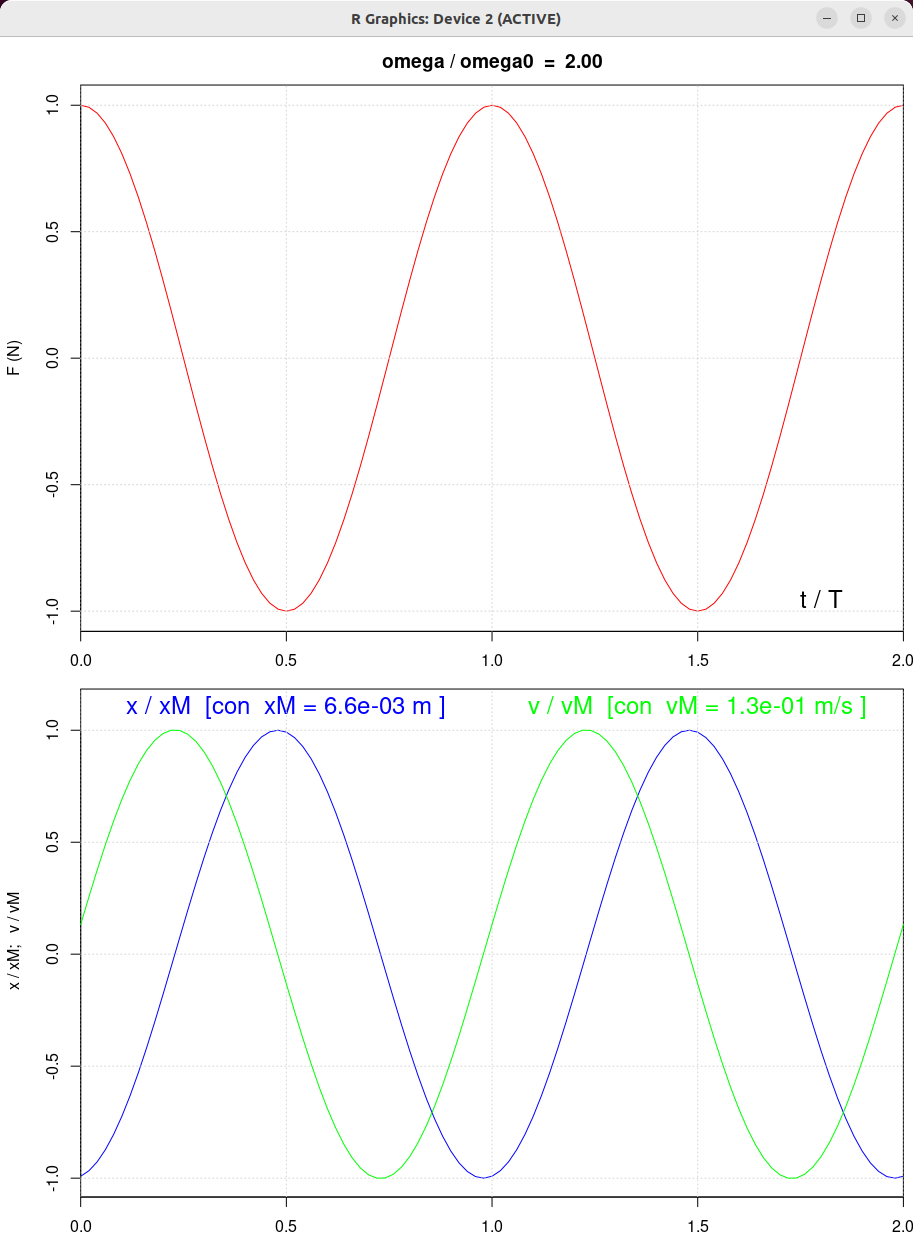
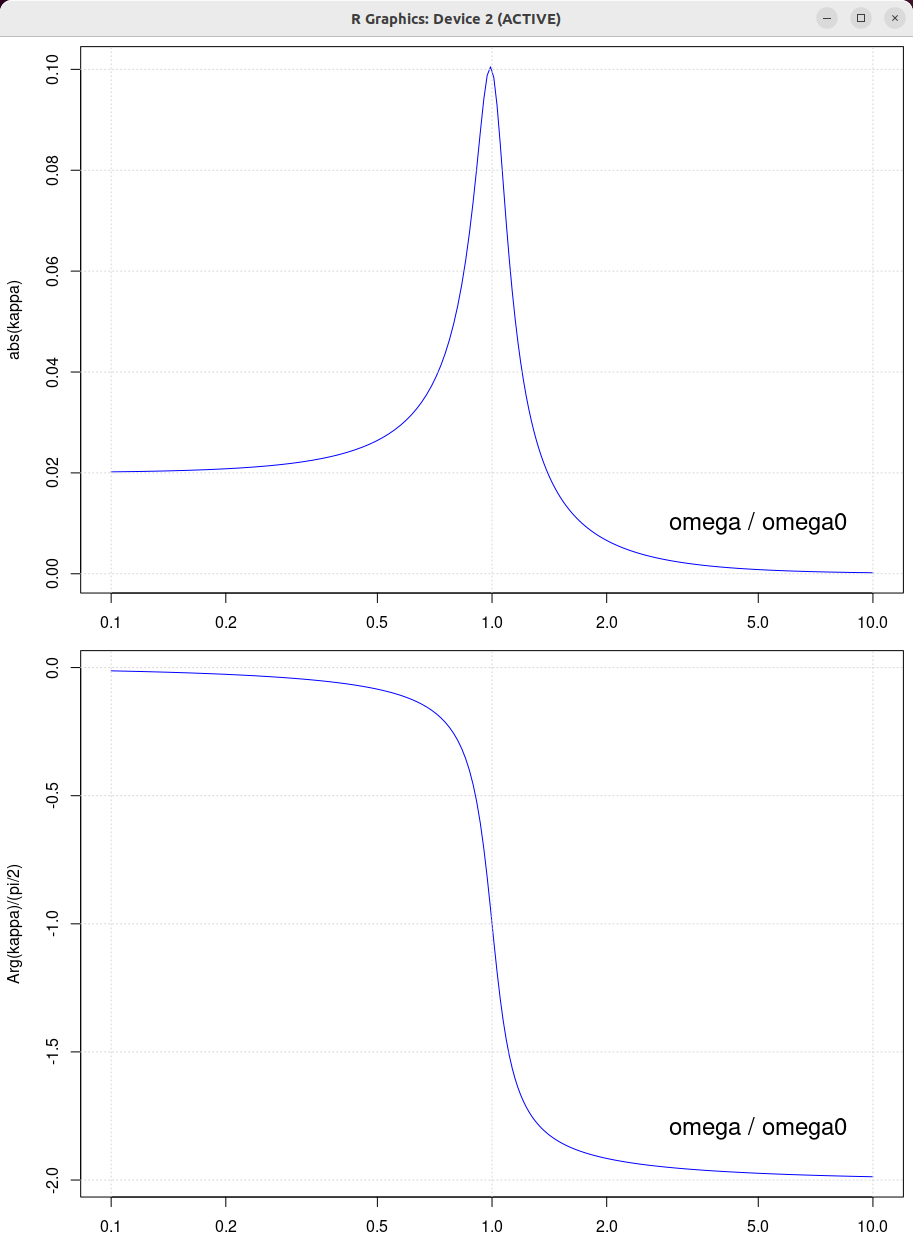
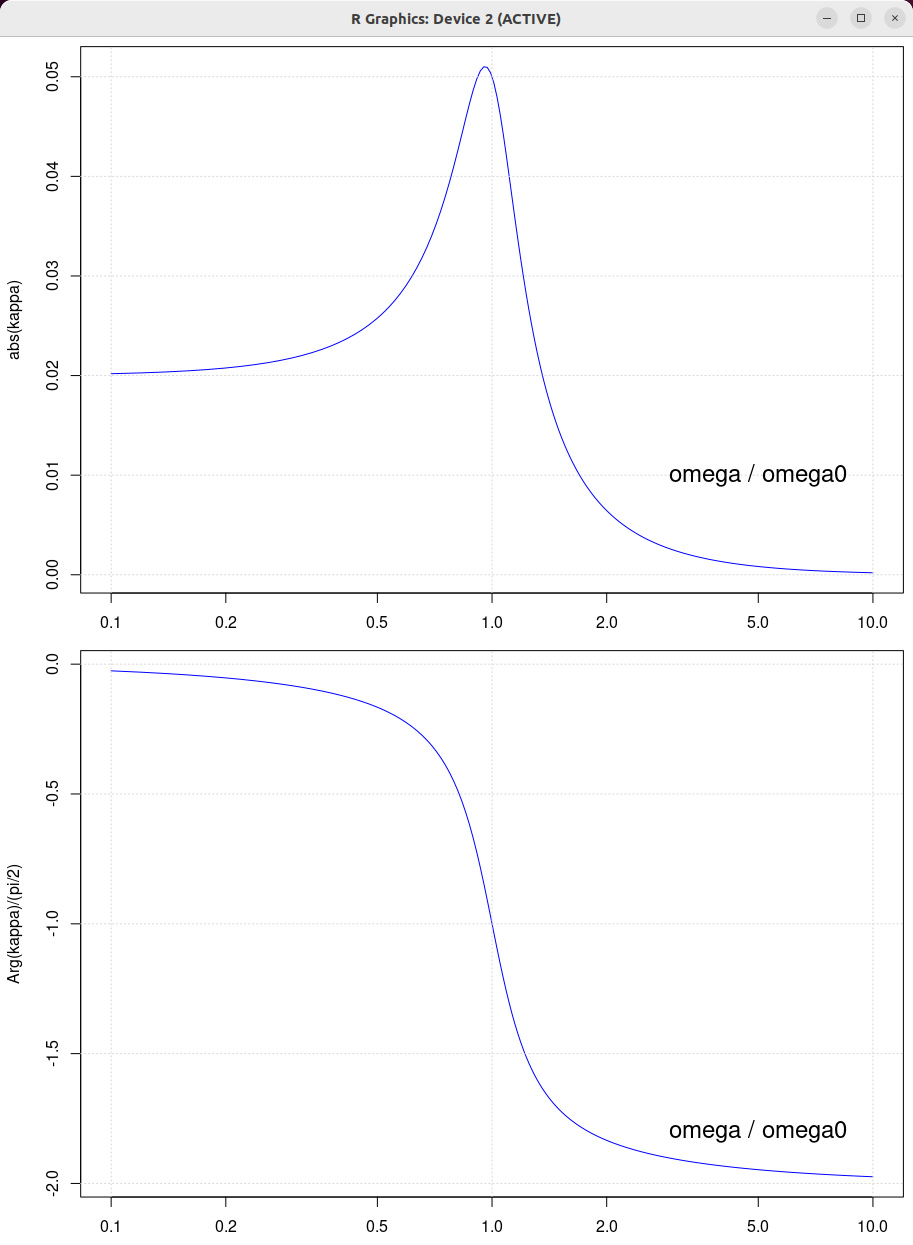
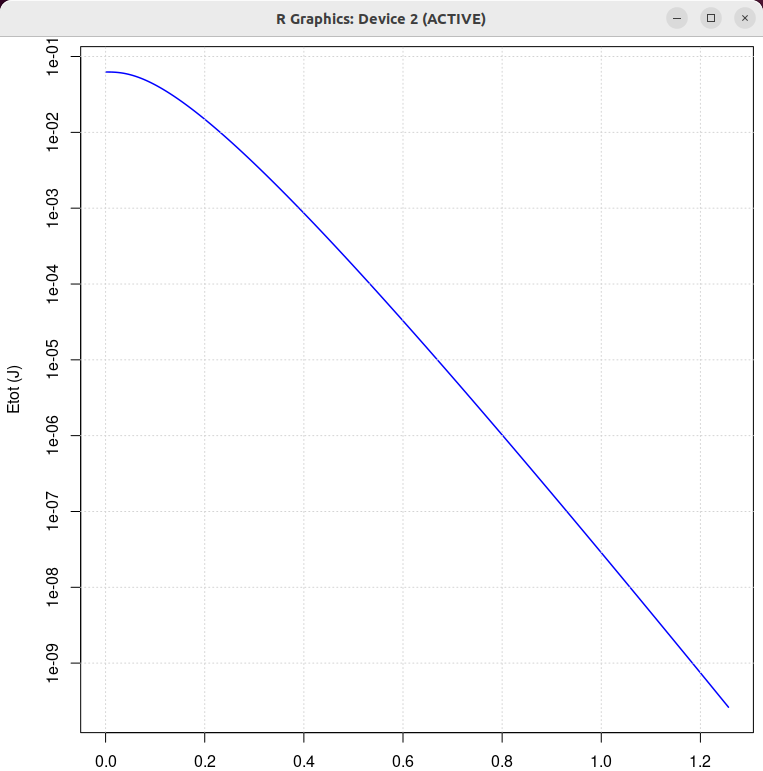
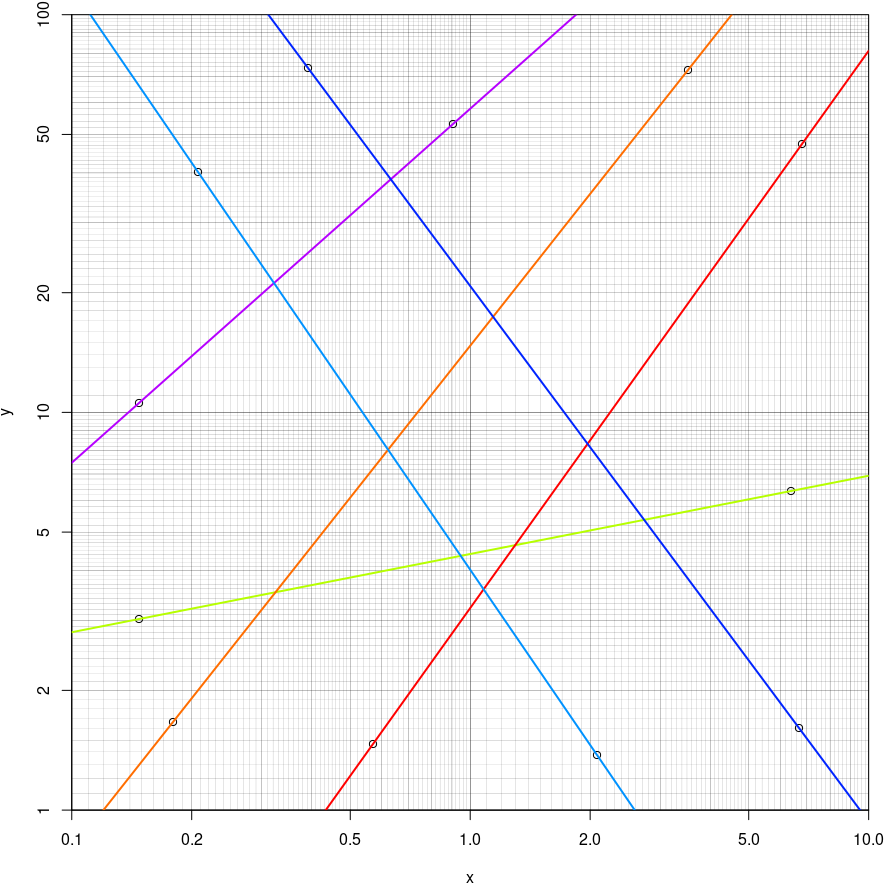
| beta = 0.5 | beta = 1.0 | beta = 2.0 |
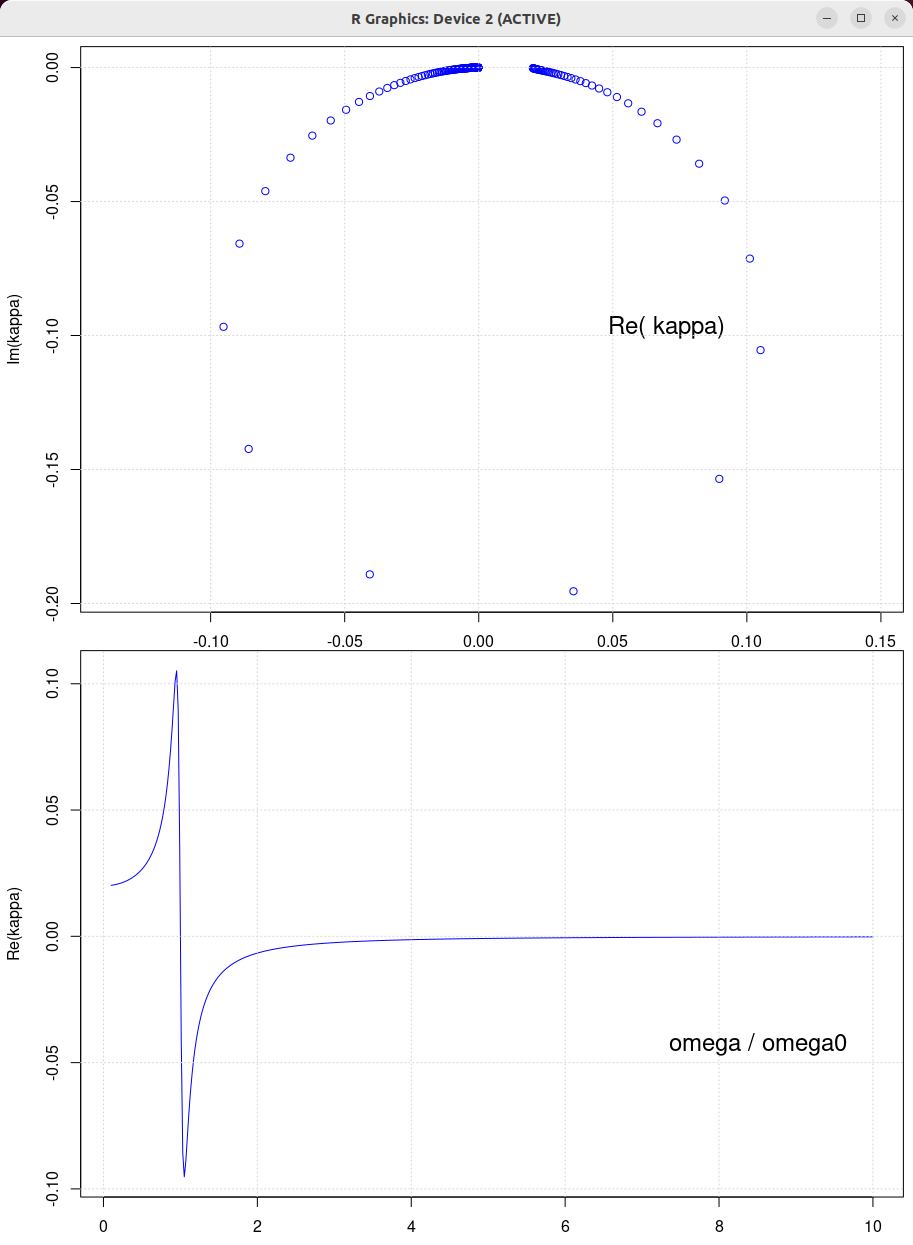
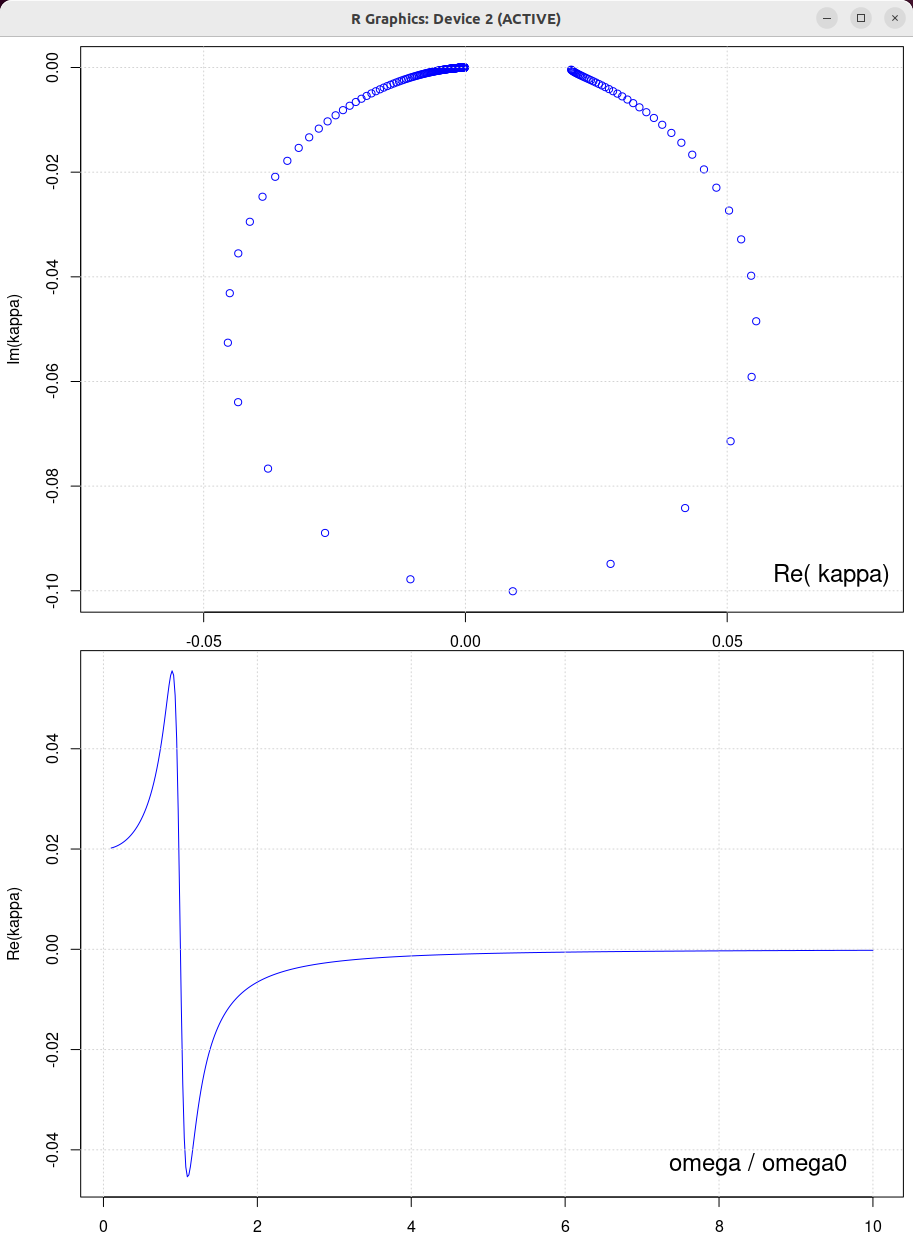
| 
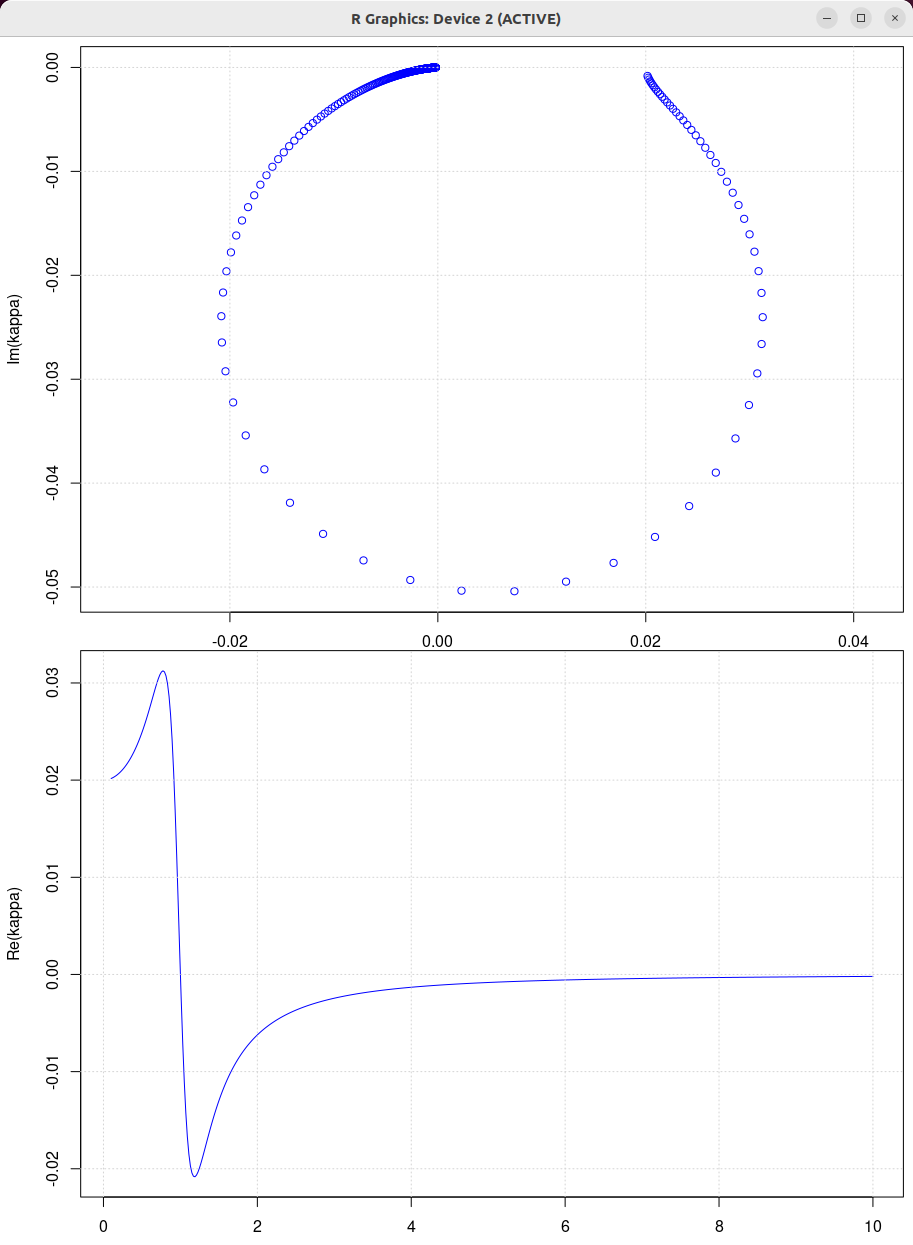
| 
|
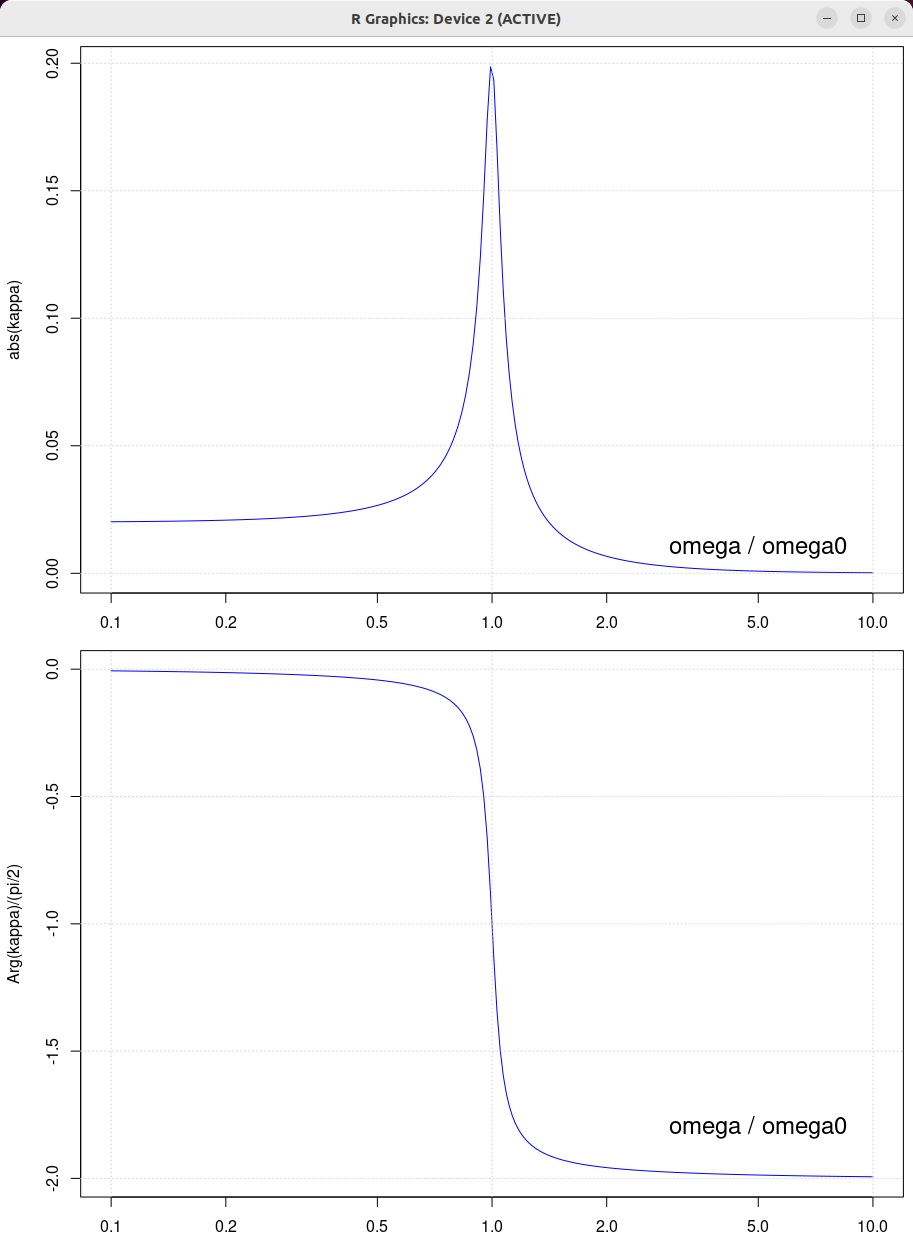
| 
| 
|
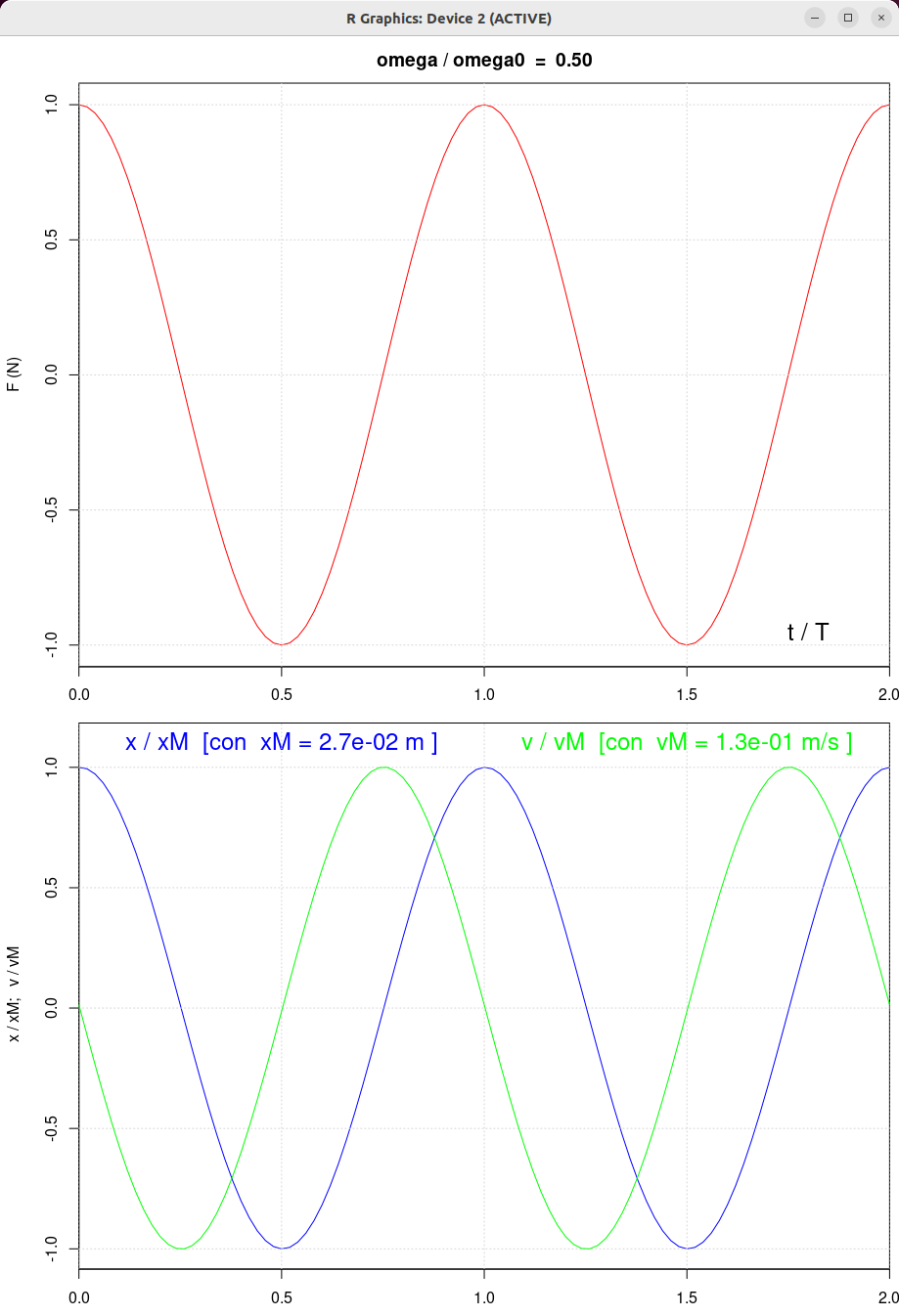
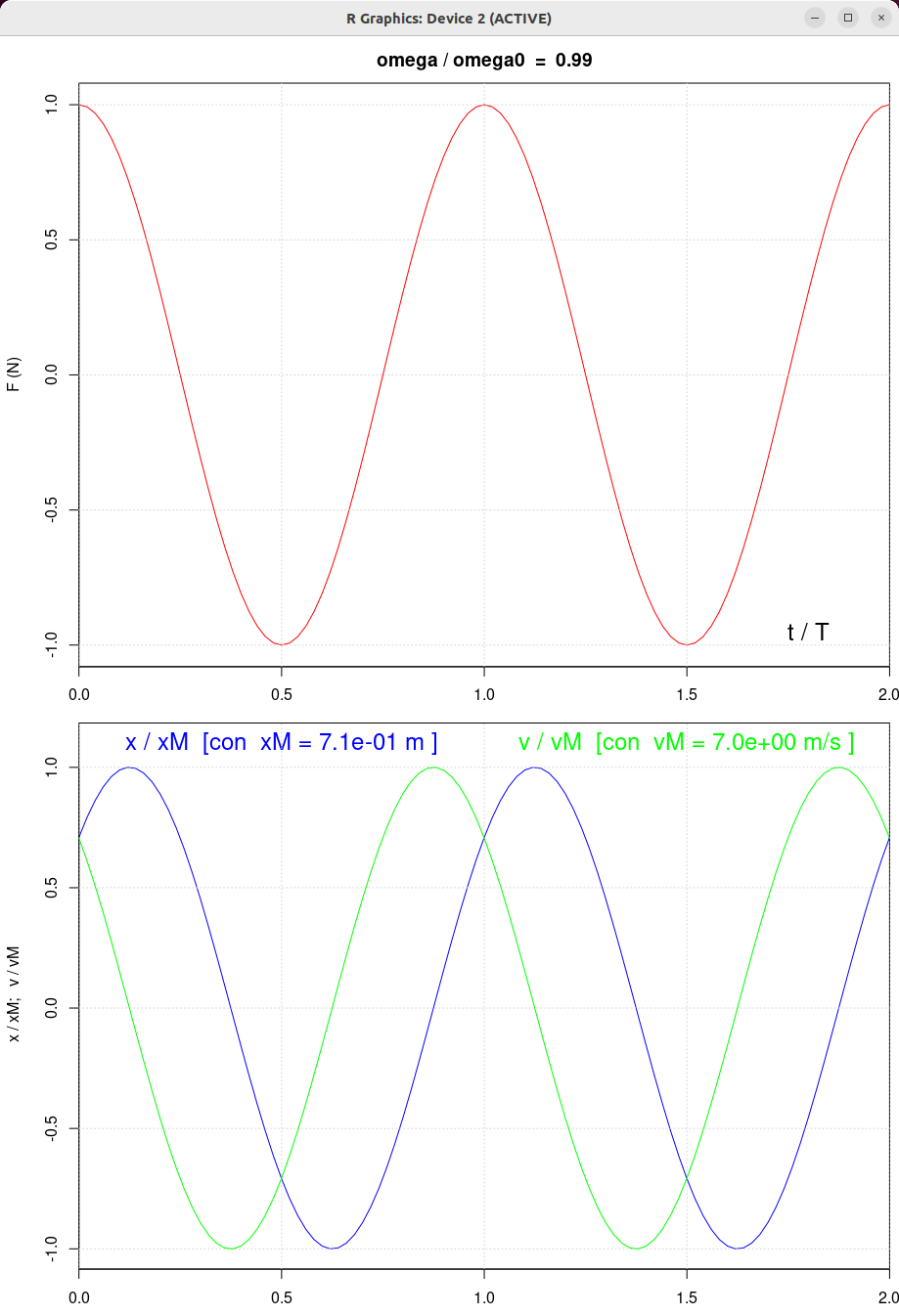
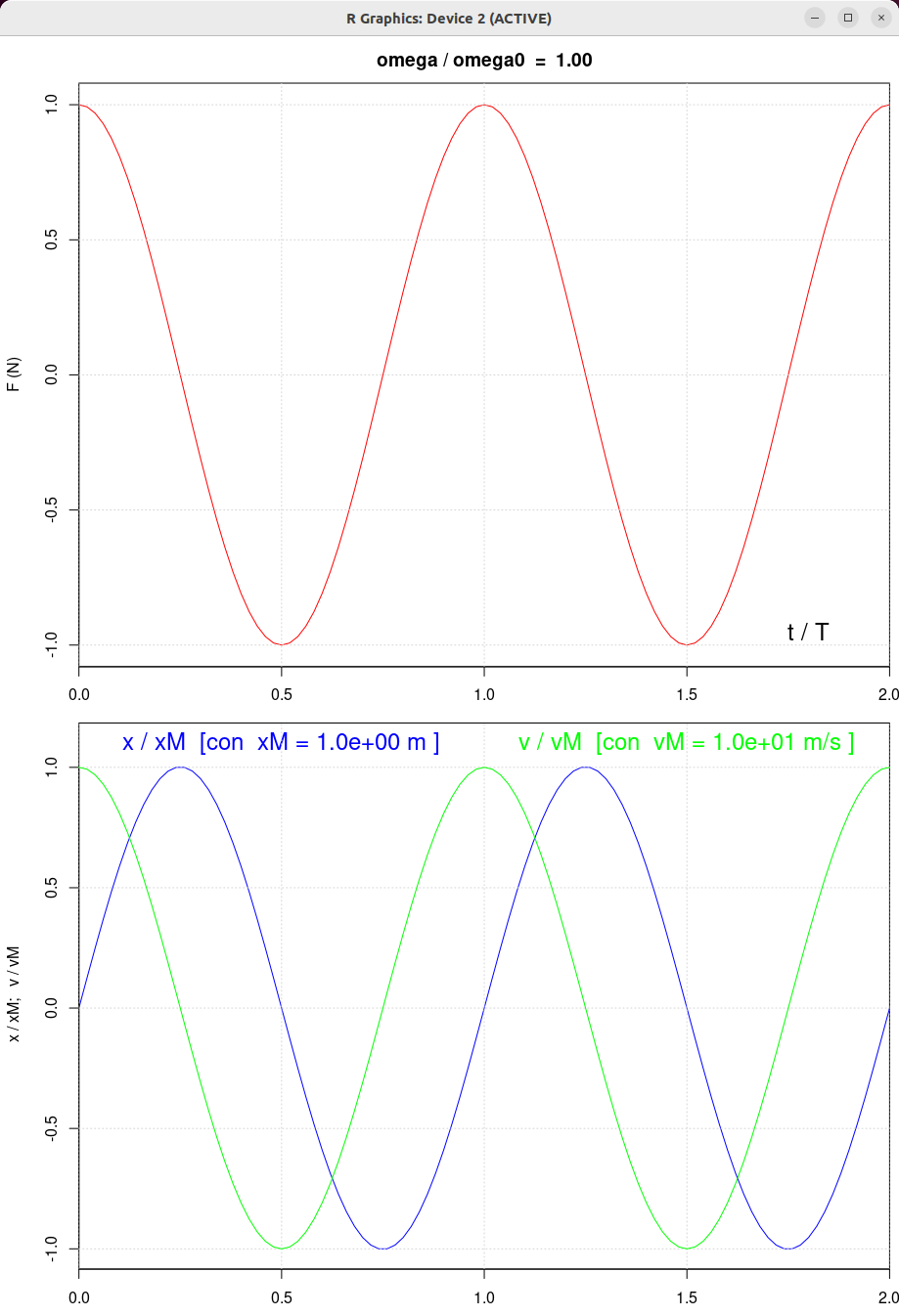
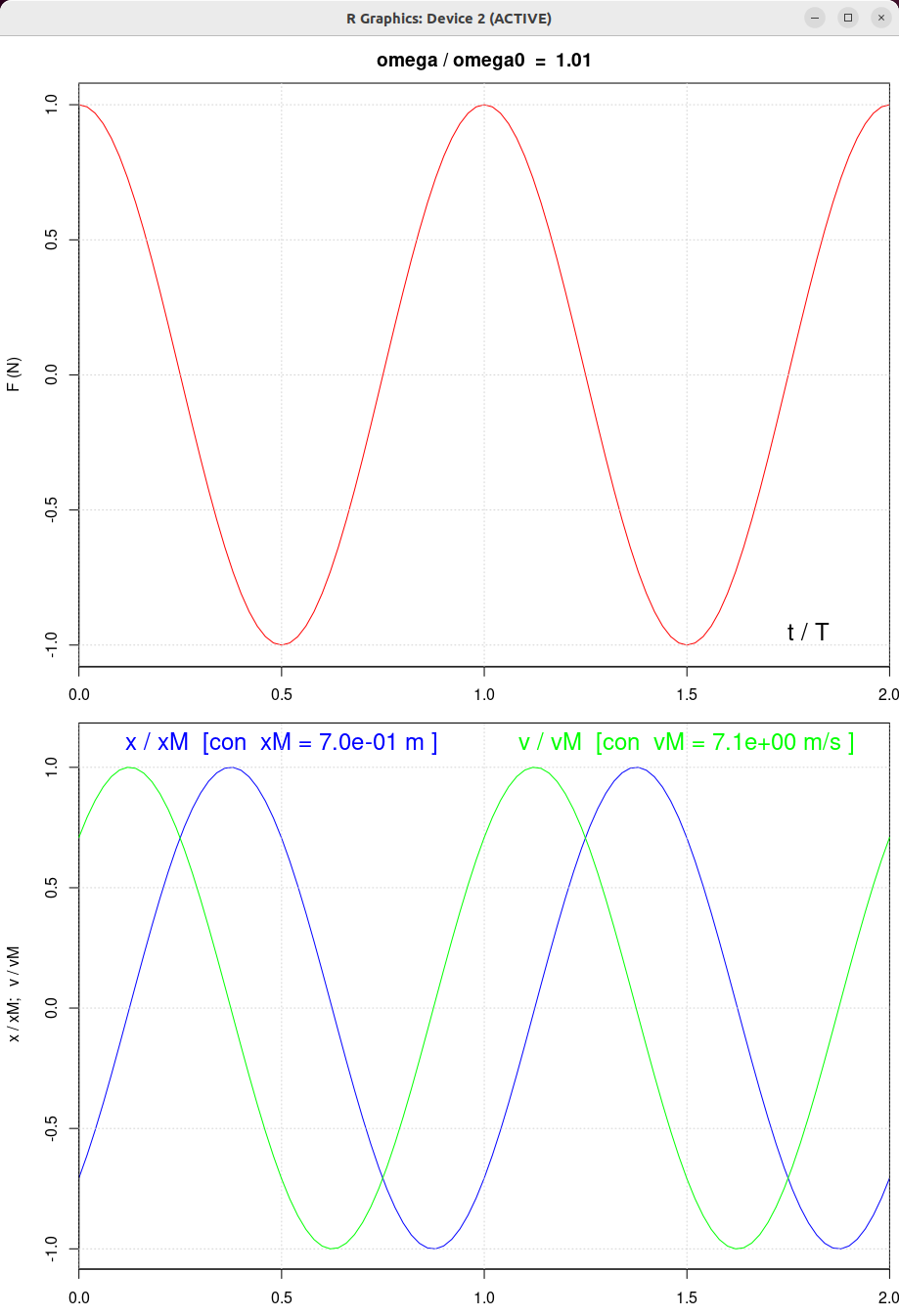
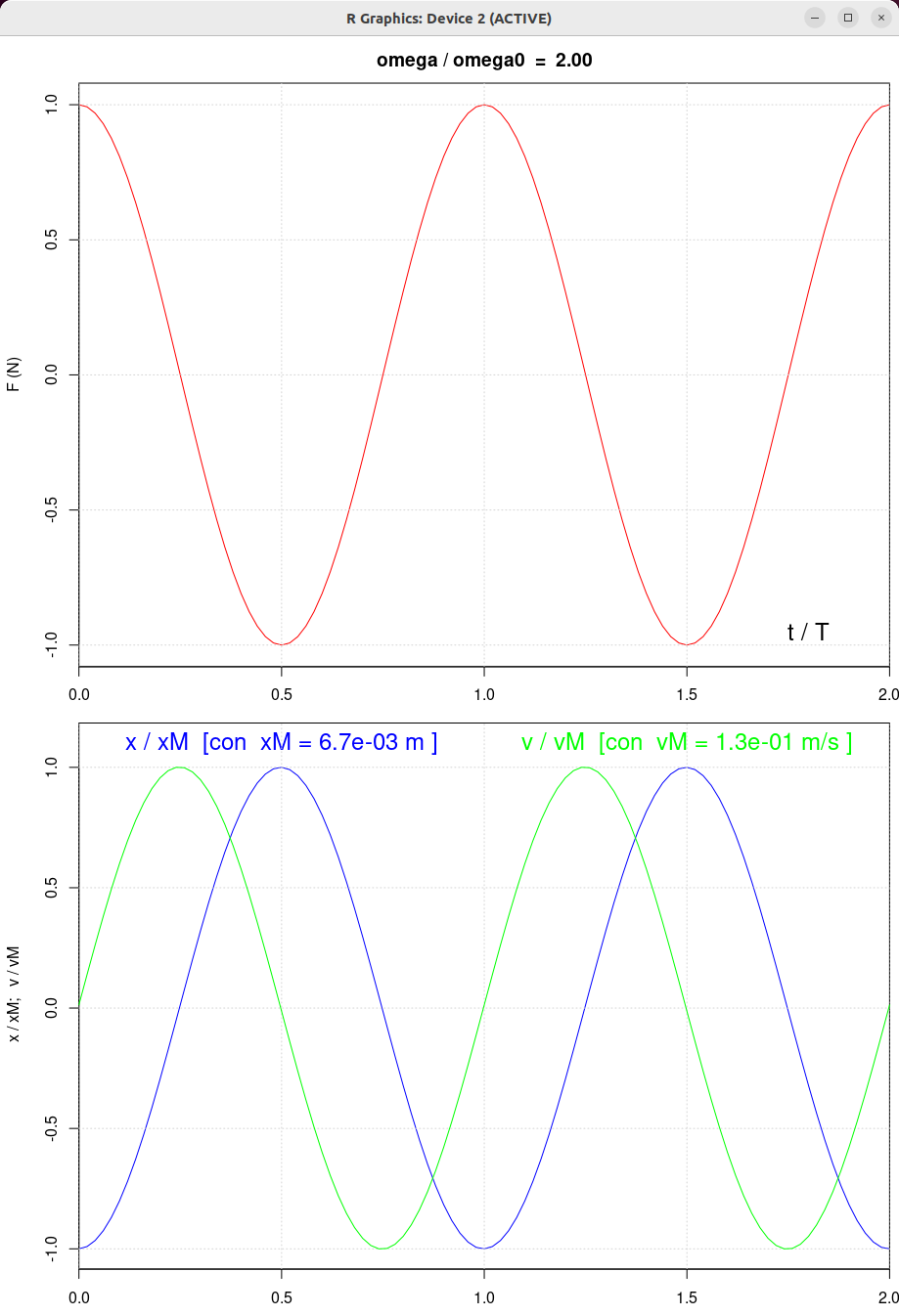

|
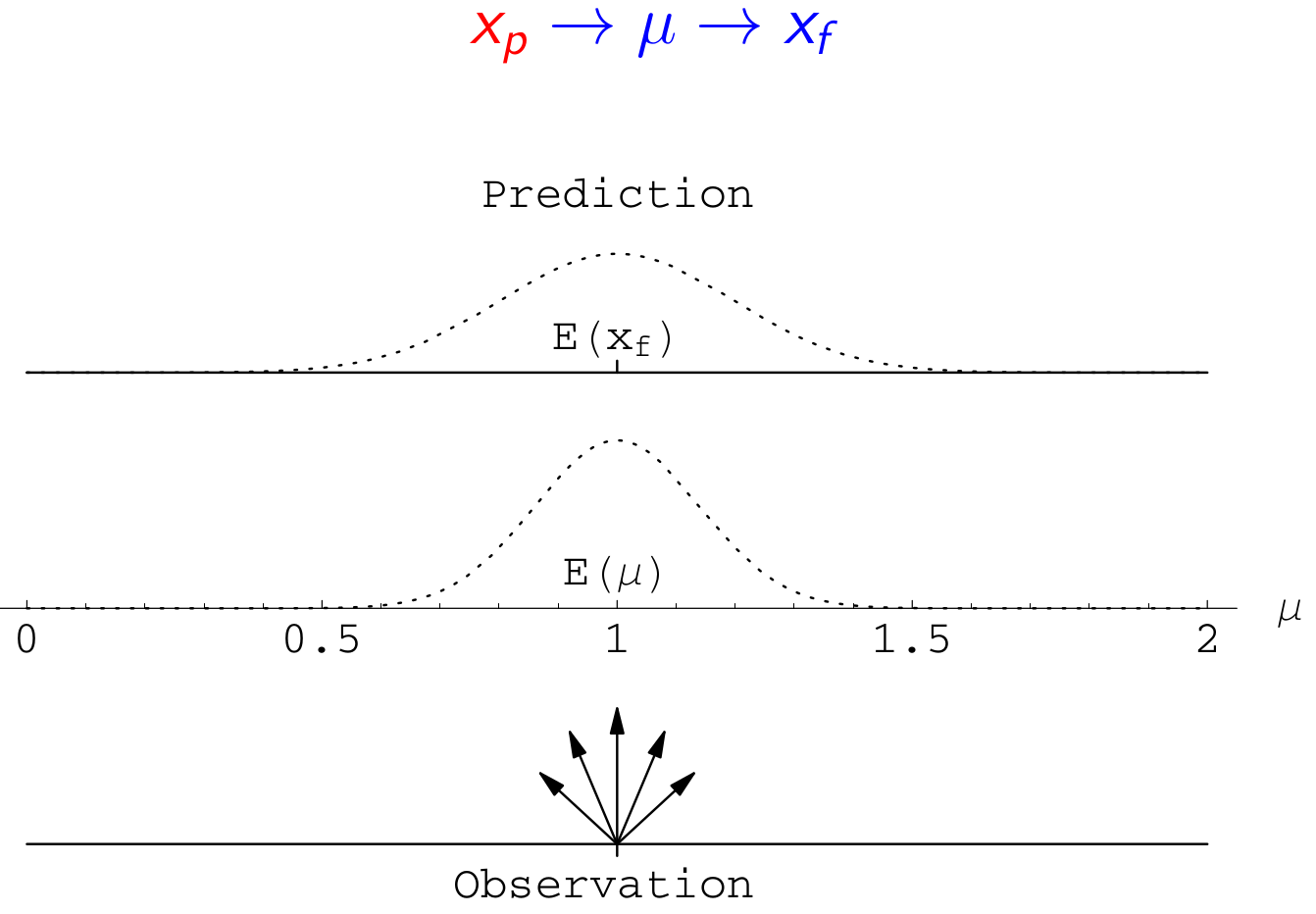
|
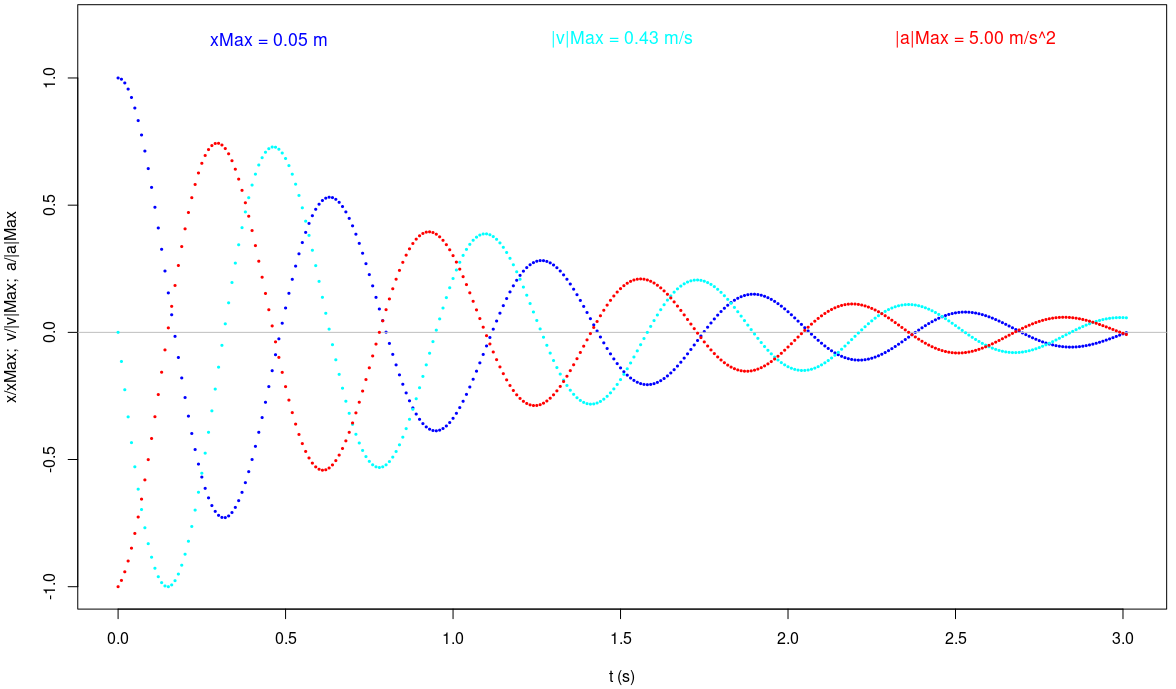
| β = 1 N/(m/s) | β = 0.5 N/(m/s) | β = 2 N/(m/s) | β = 10 N/(m/s) |
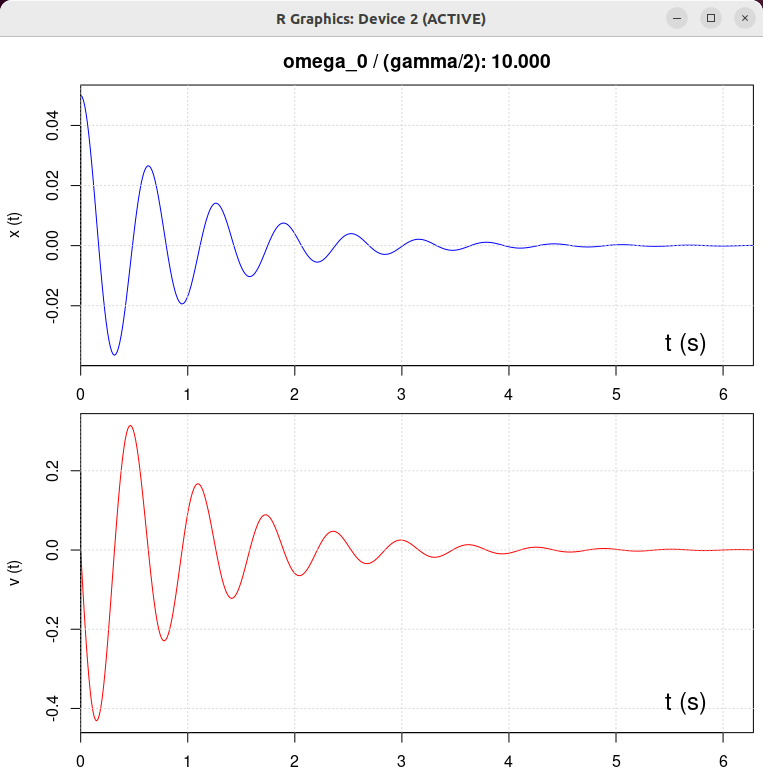
|
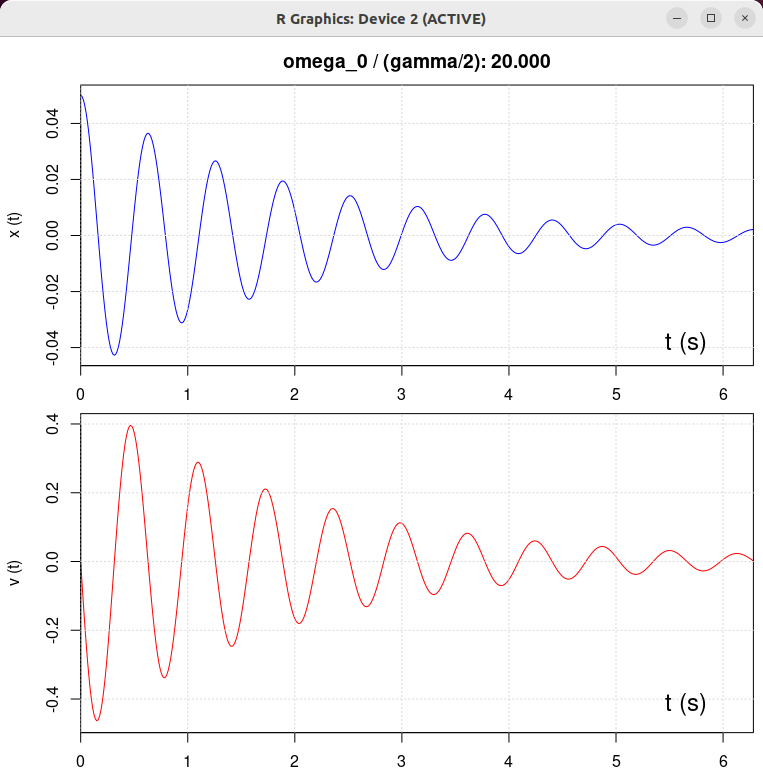
|
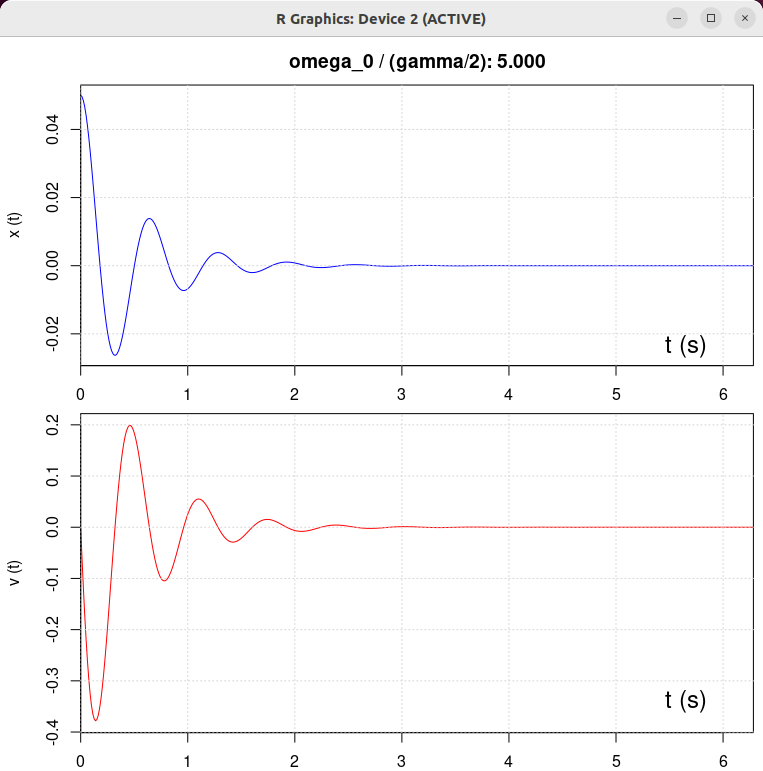
|
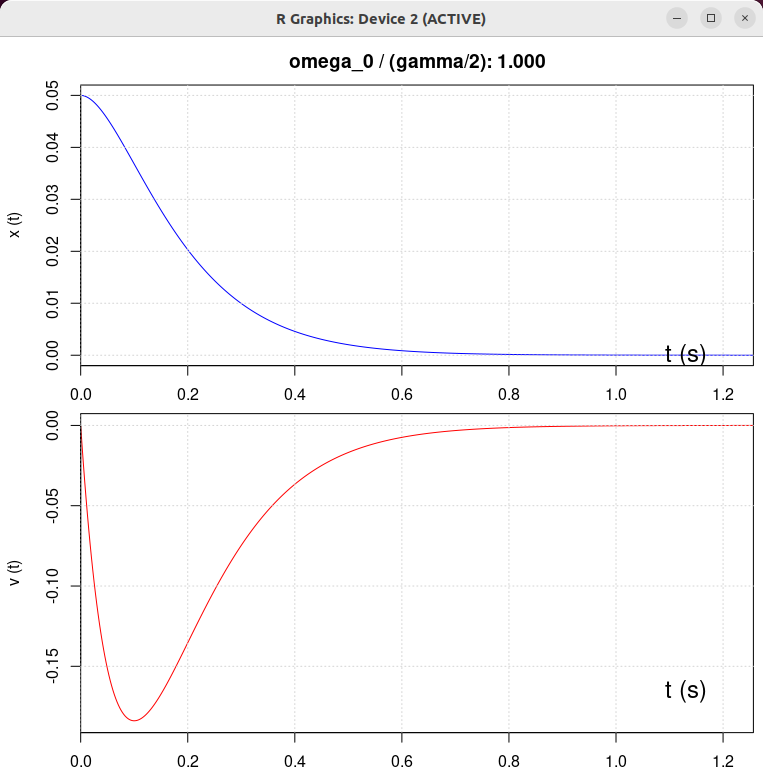
|
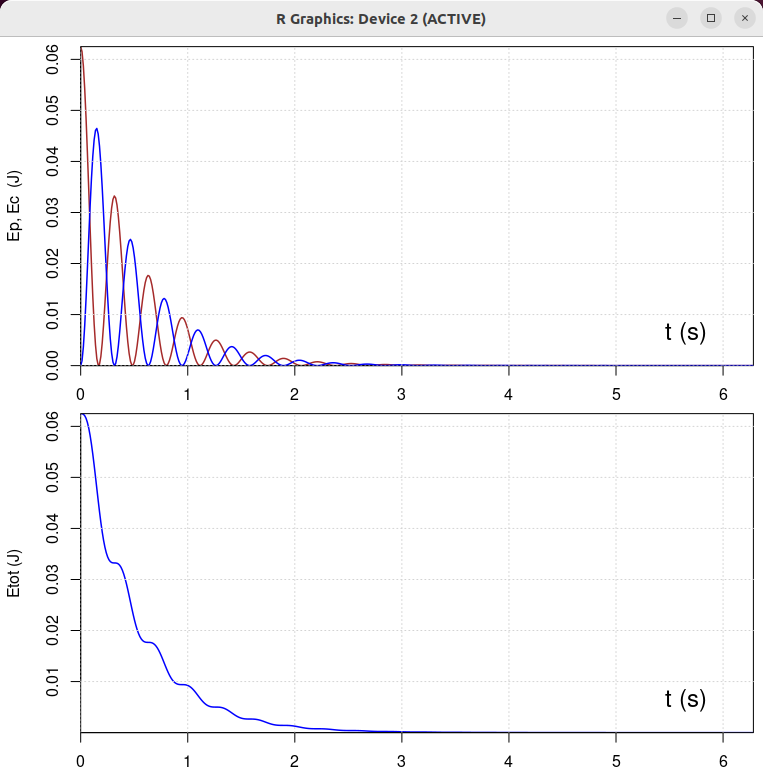
|
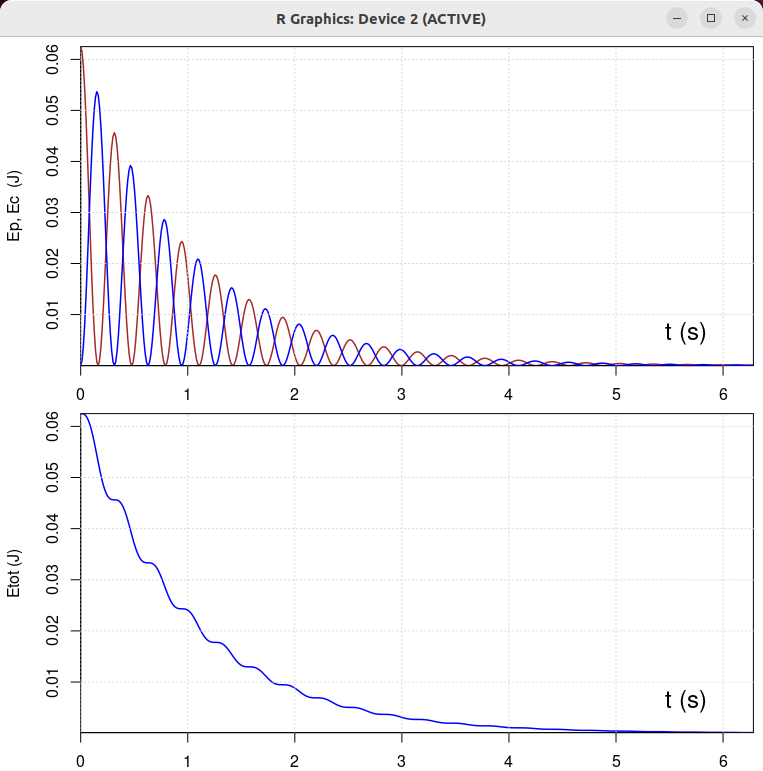
|
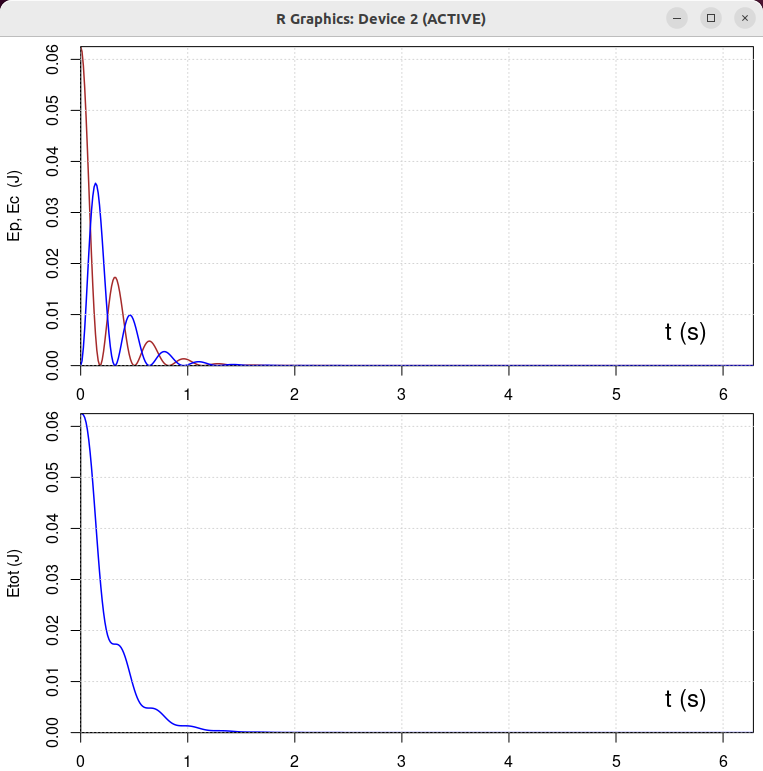
|
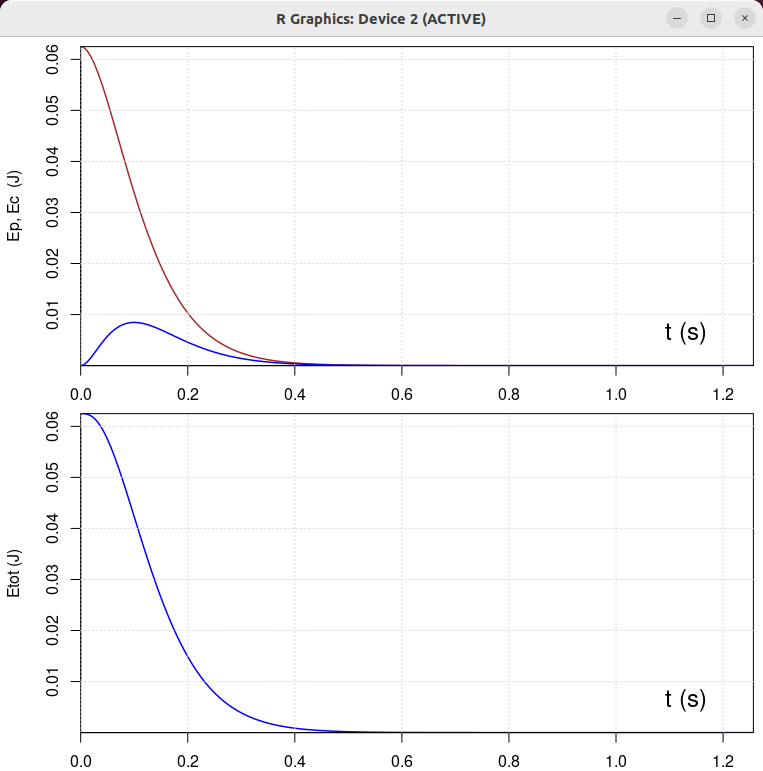
|
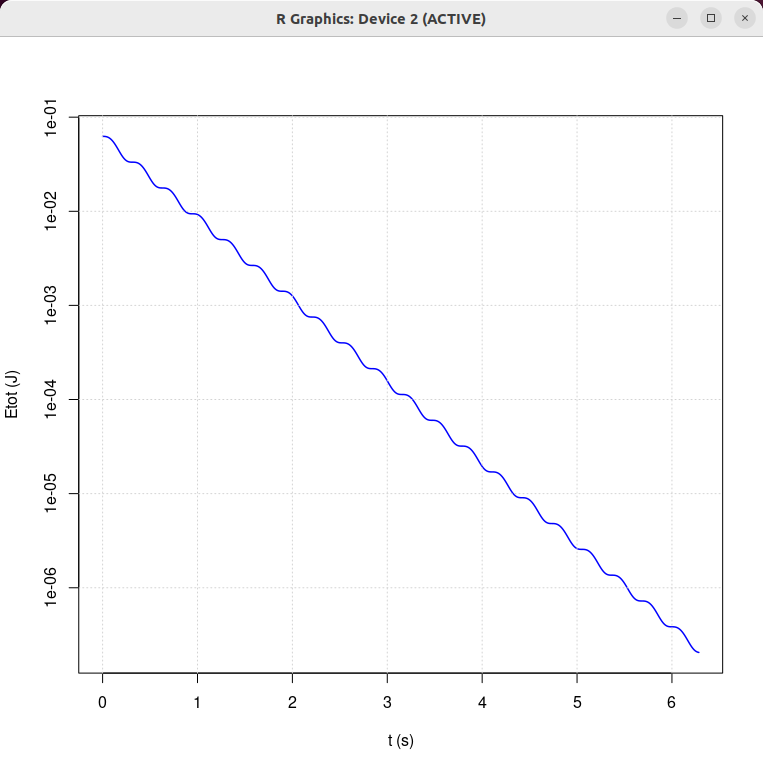
|
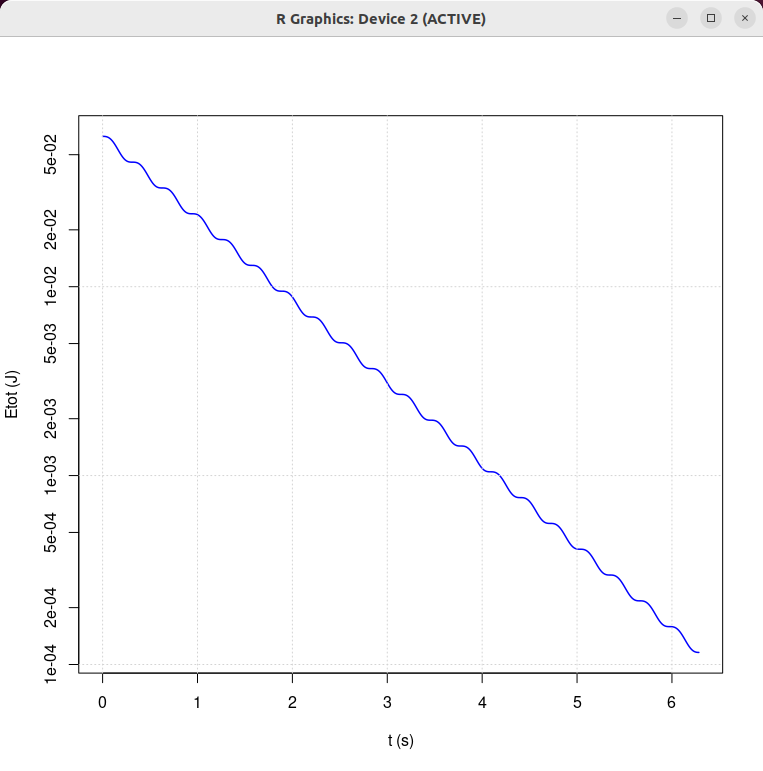
|
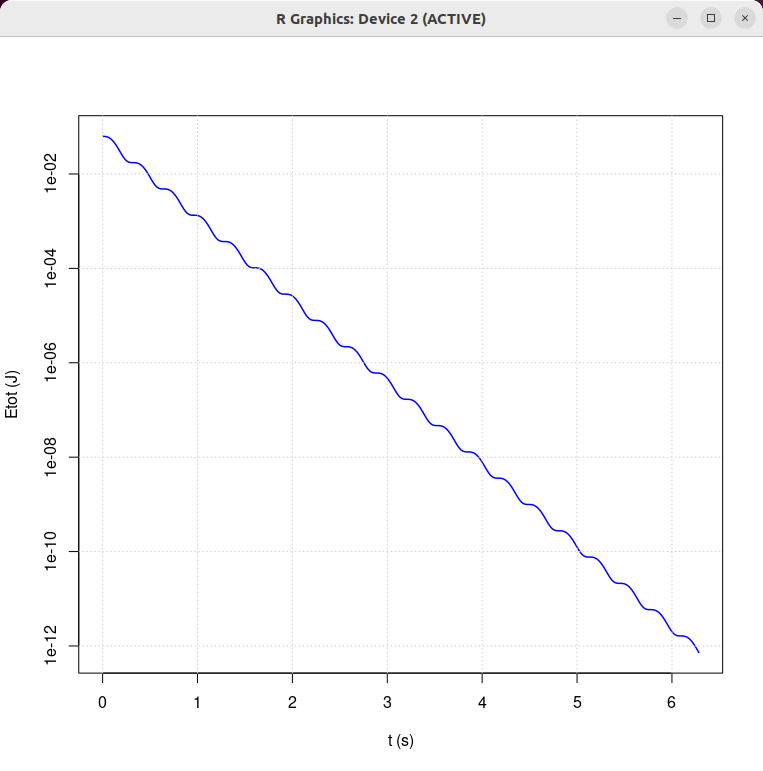
|
|











.jpg)



 |
 |

 |
 |









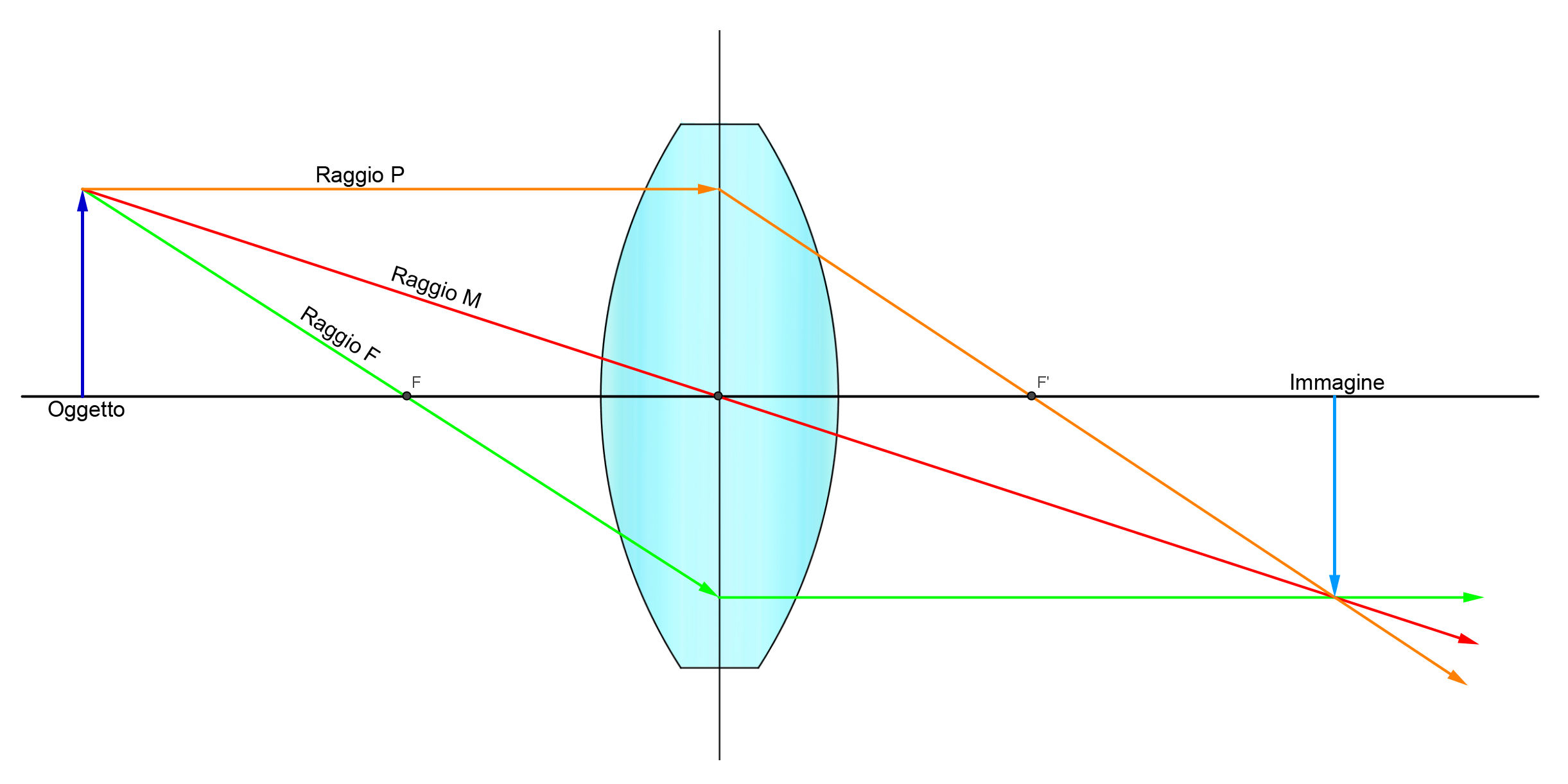 |
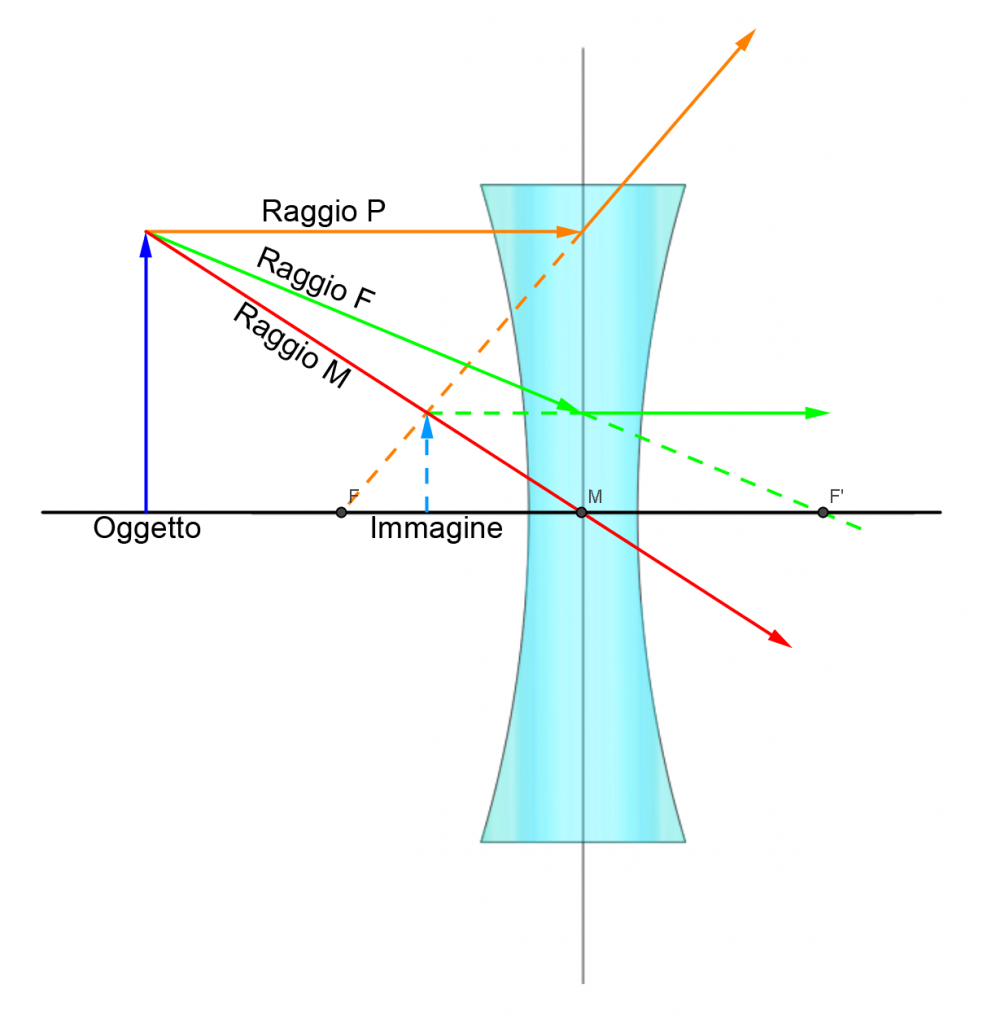 |
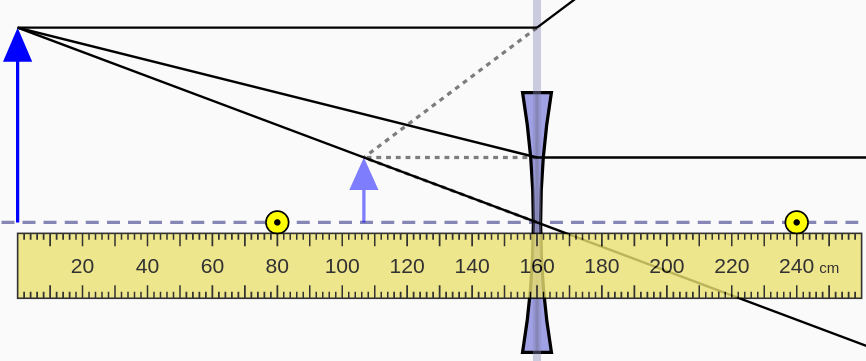
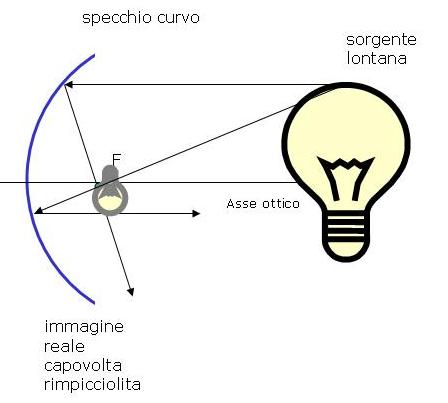 |
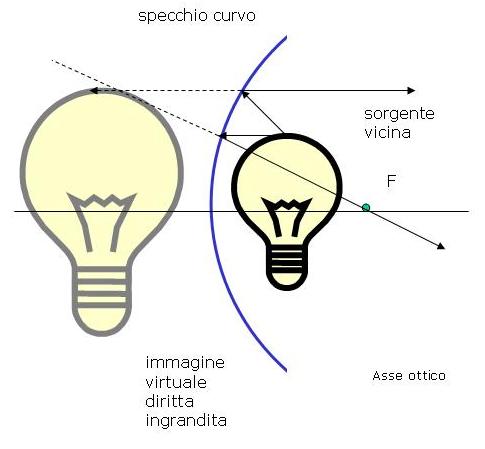 |
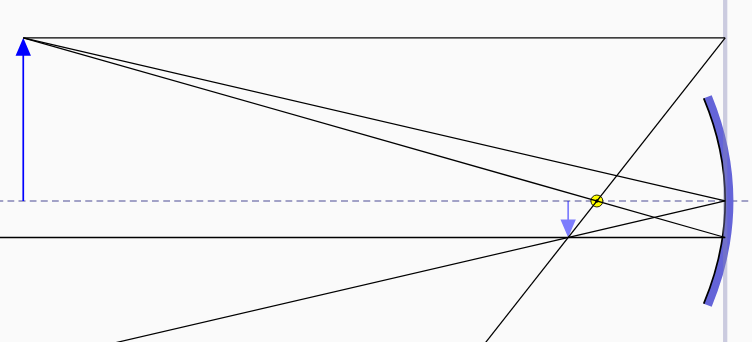
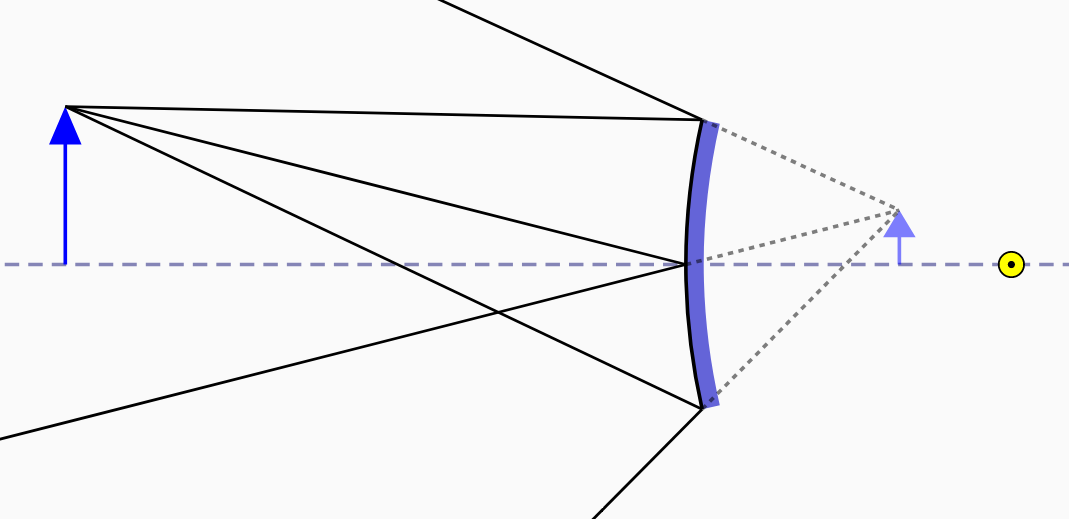


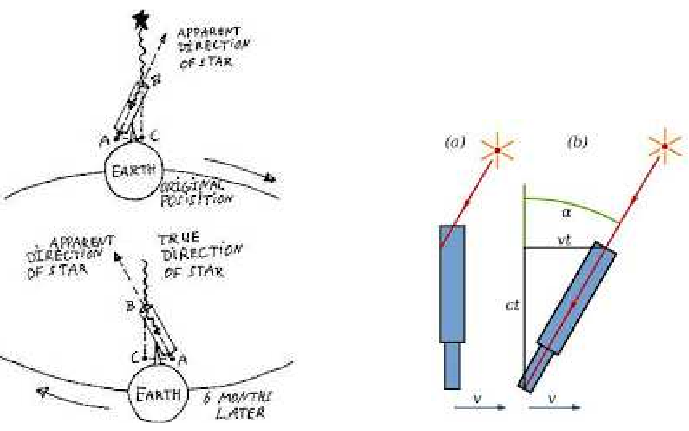
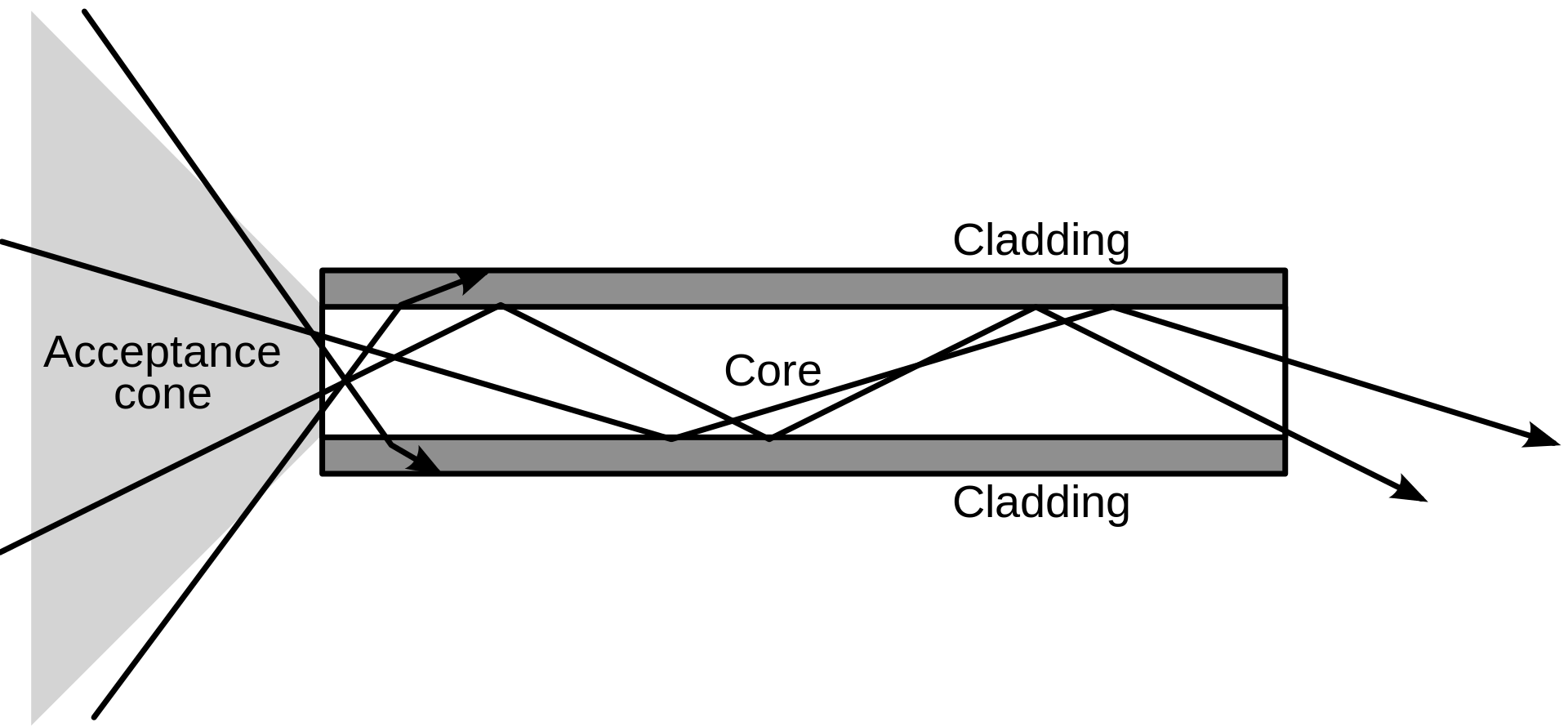
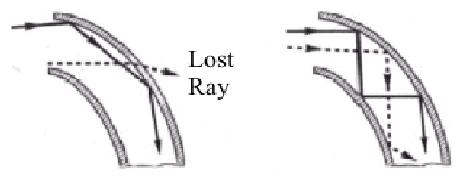


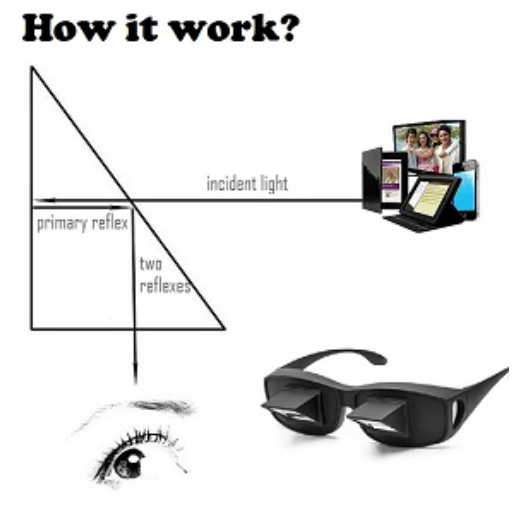



 |
 |

| |
|
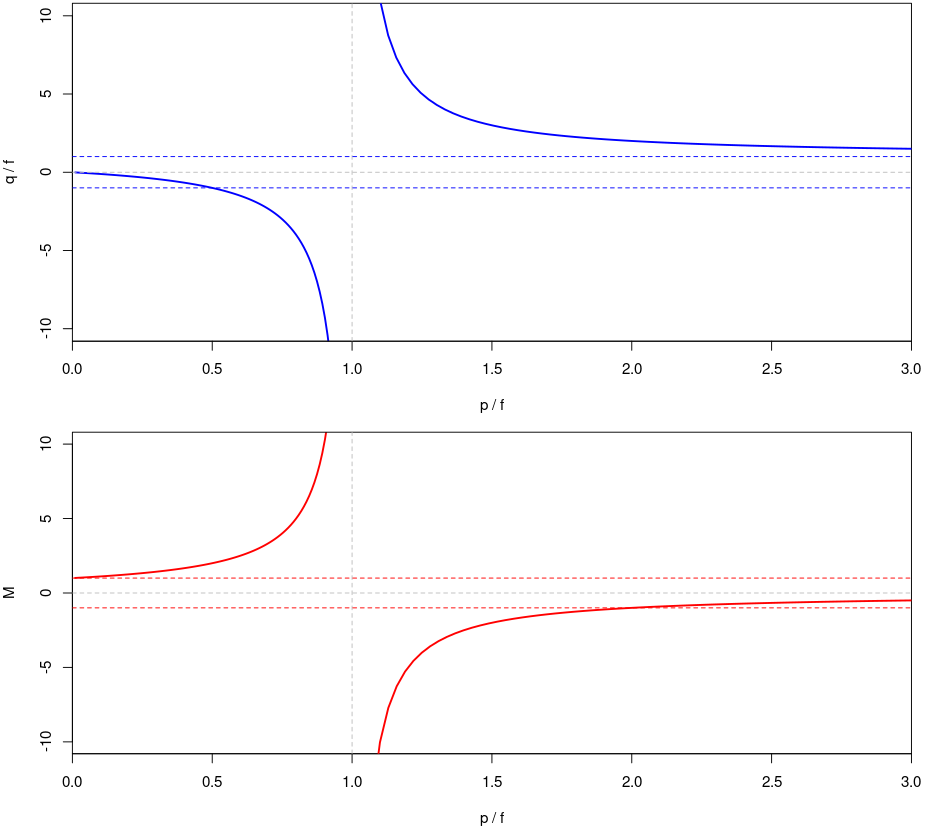
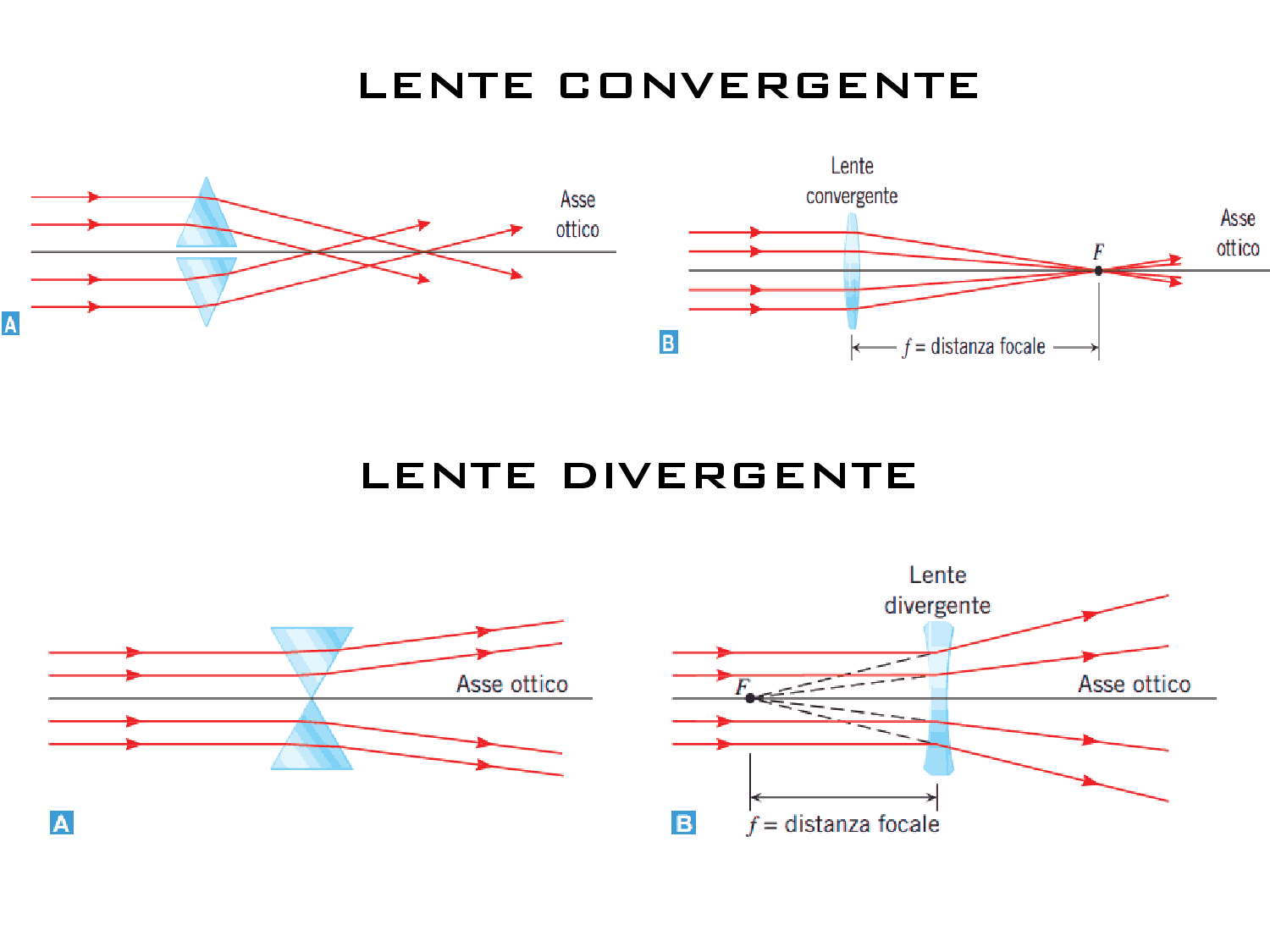
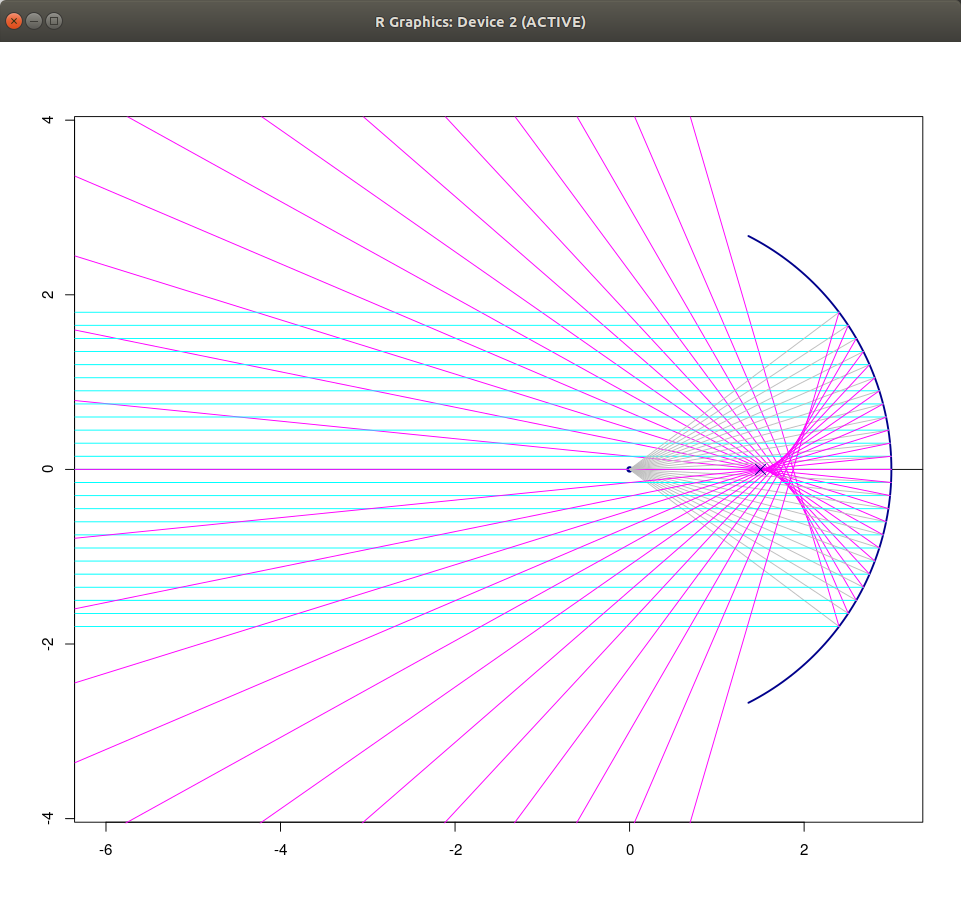
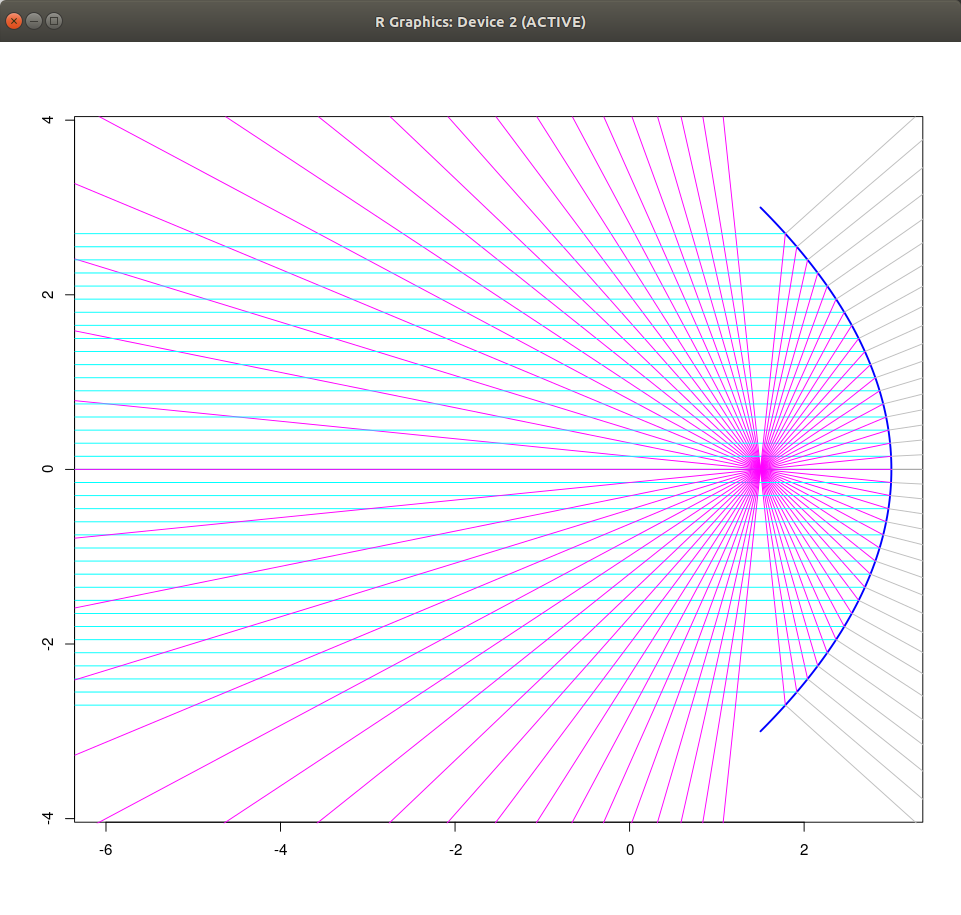
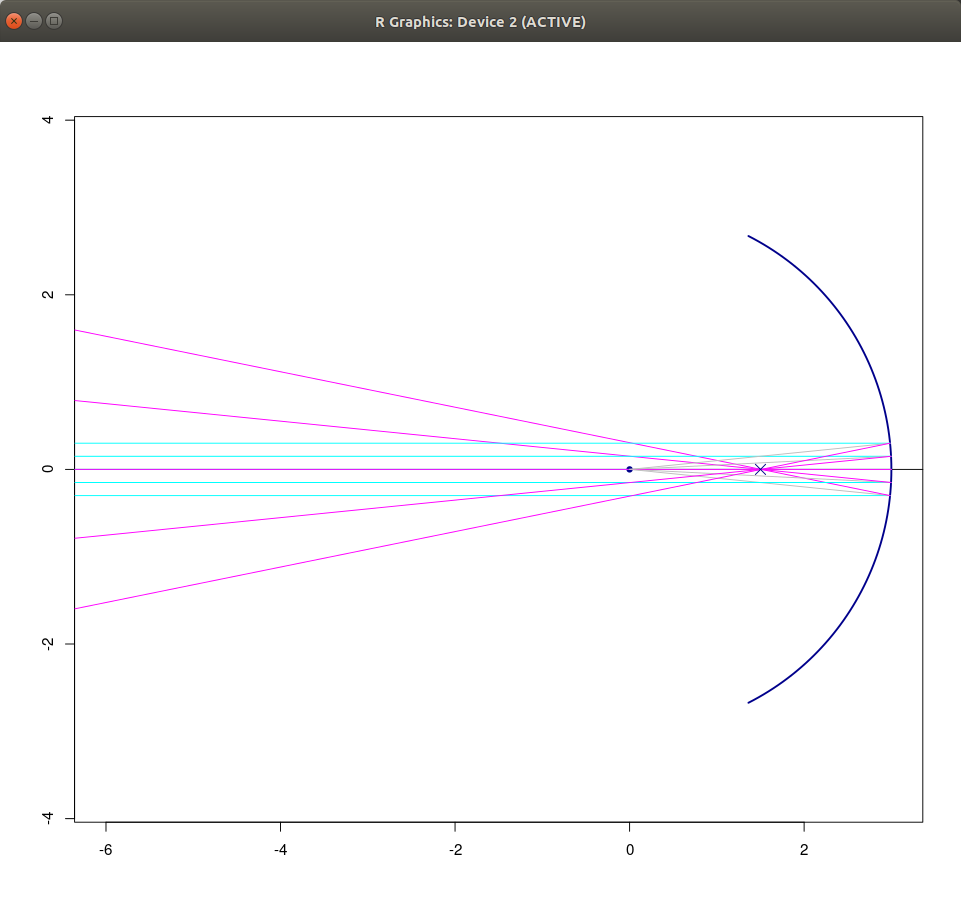
| oggetto oltre il fuoco | oggetto fra specchio e fuoco |
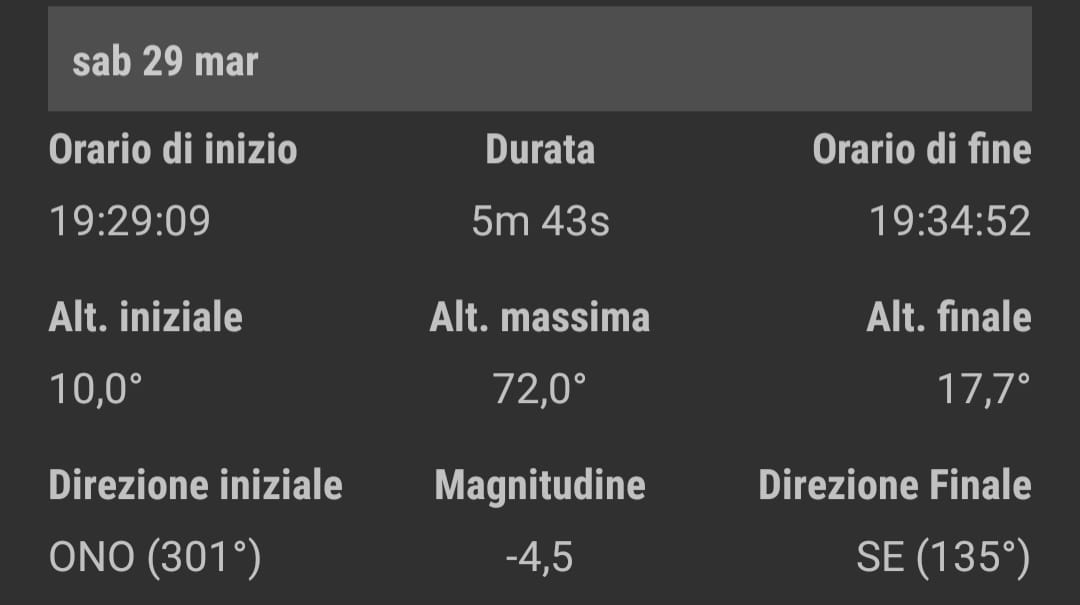
 Arcobaleno doppio (19:34) |

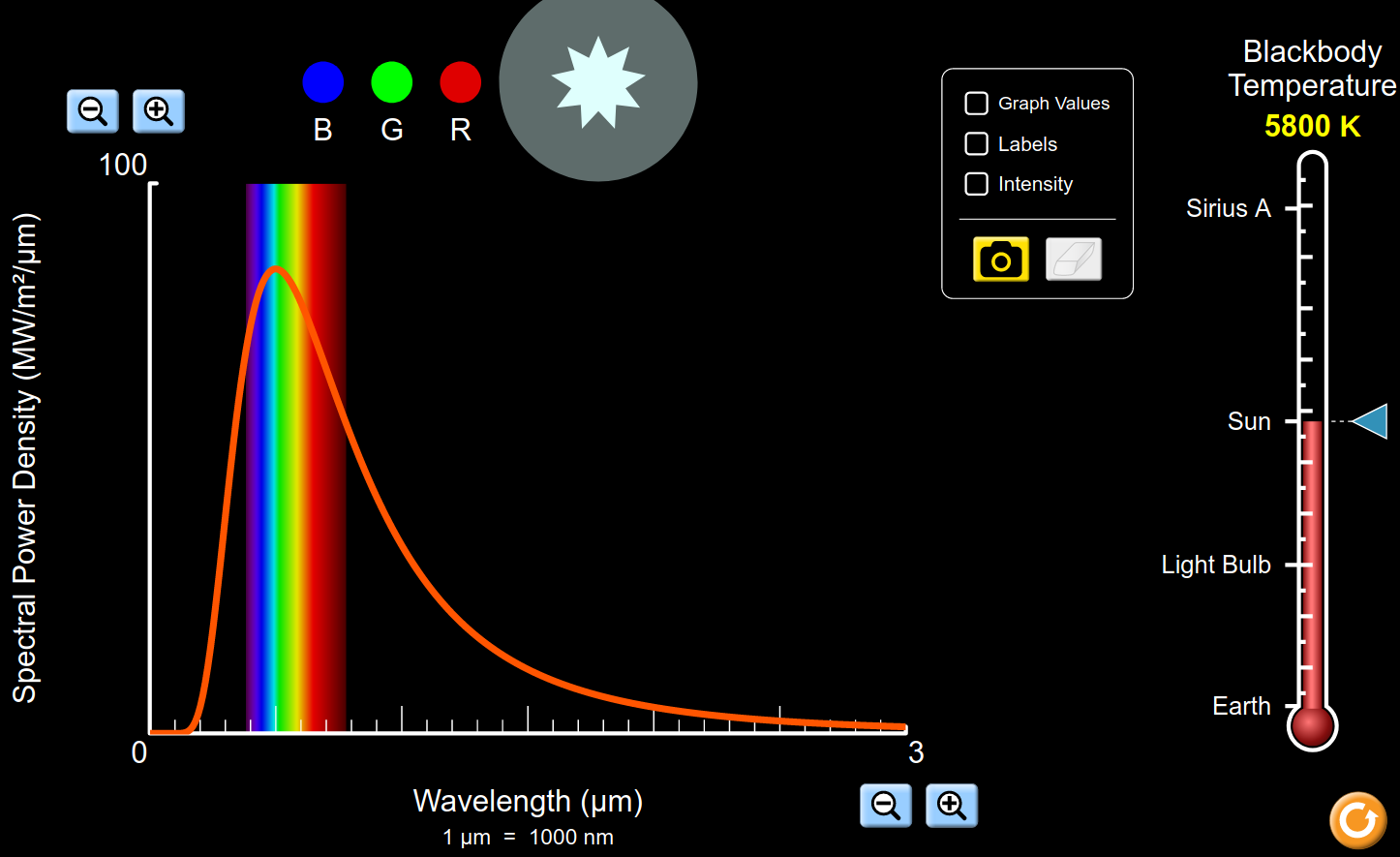
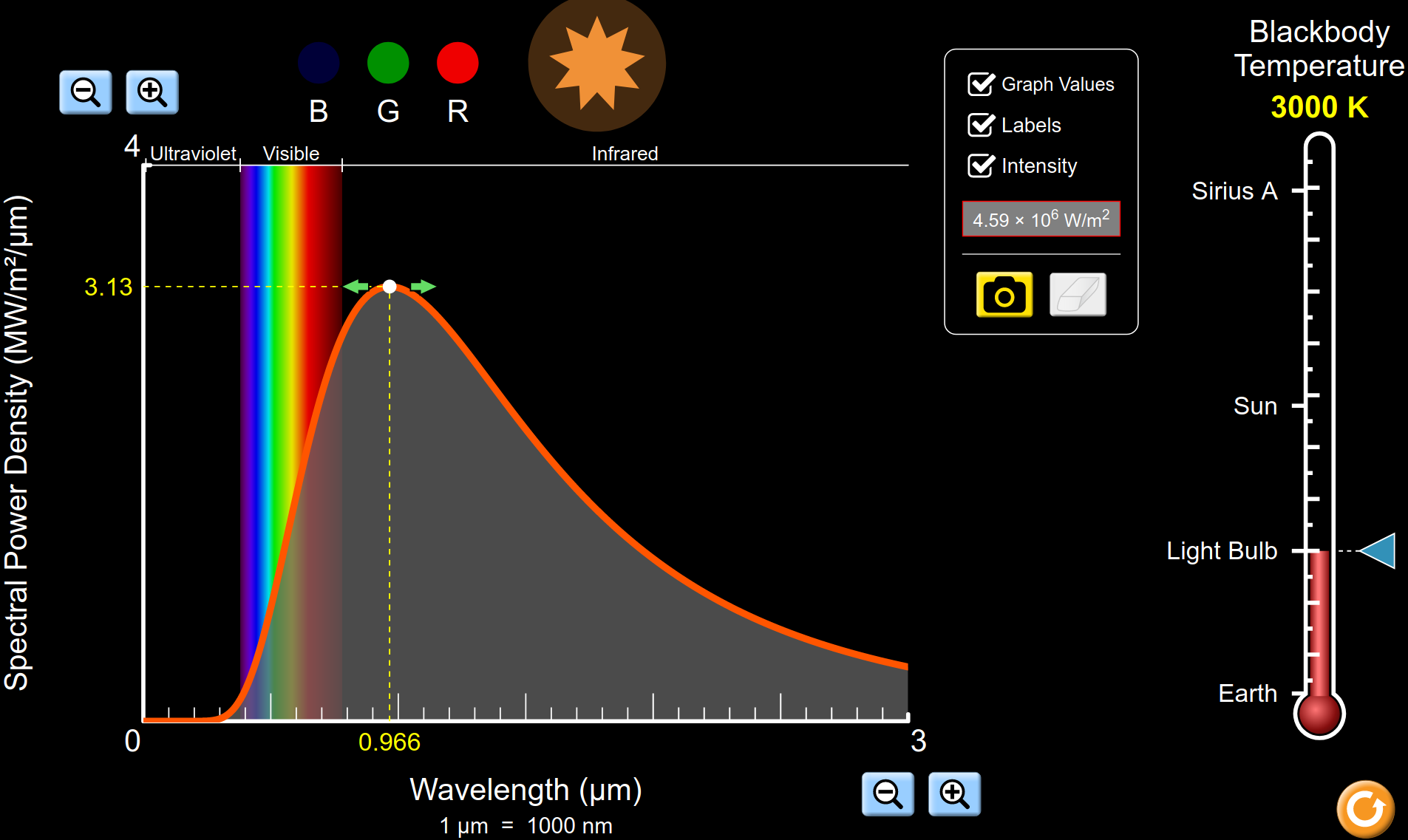
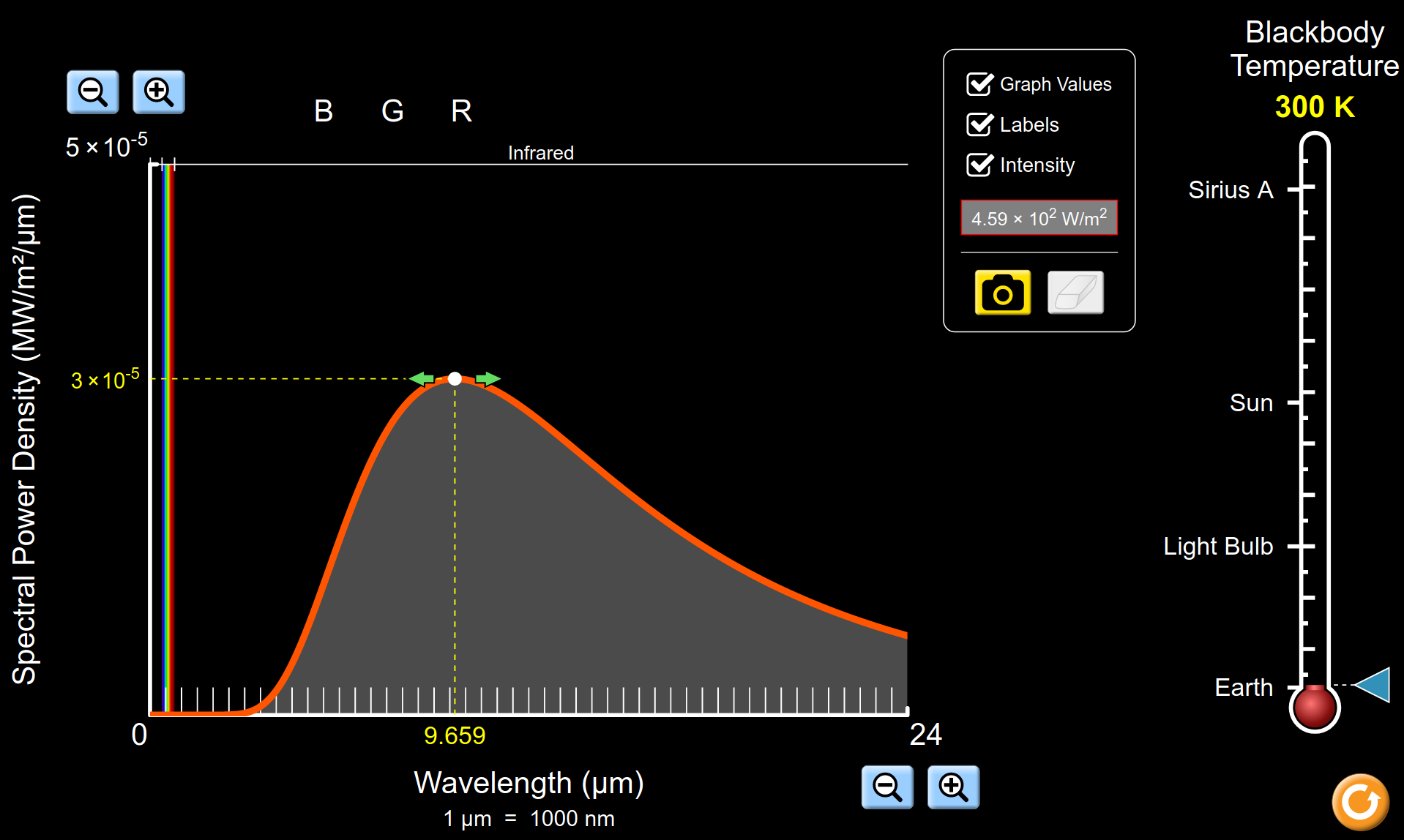
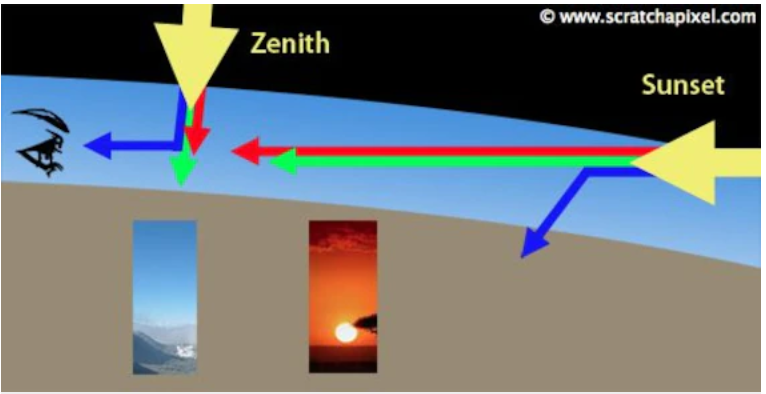
Cielo rosso e sole schiacciato (19:56) |
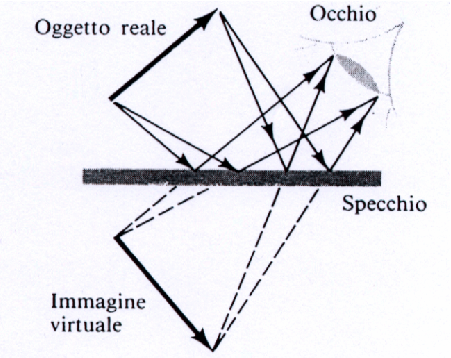
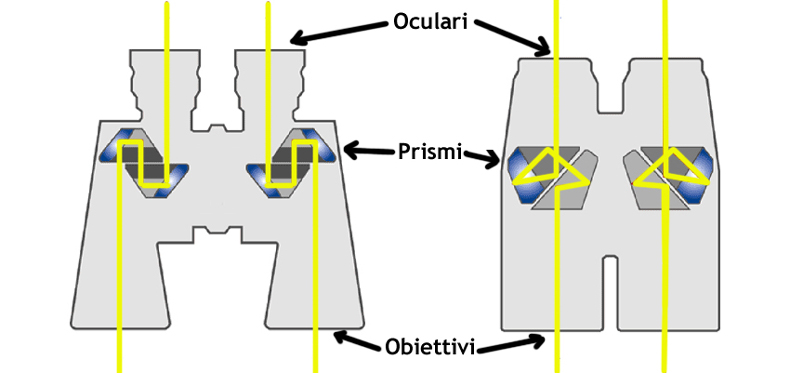

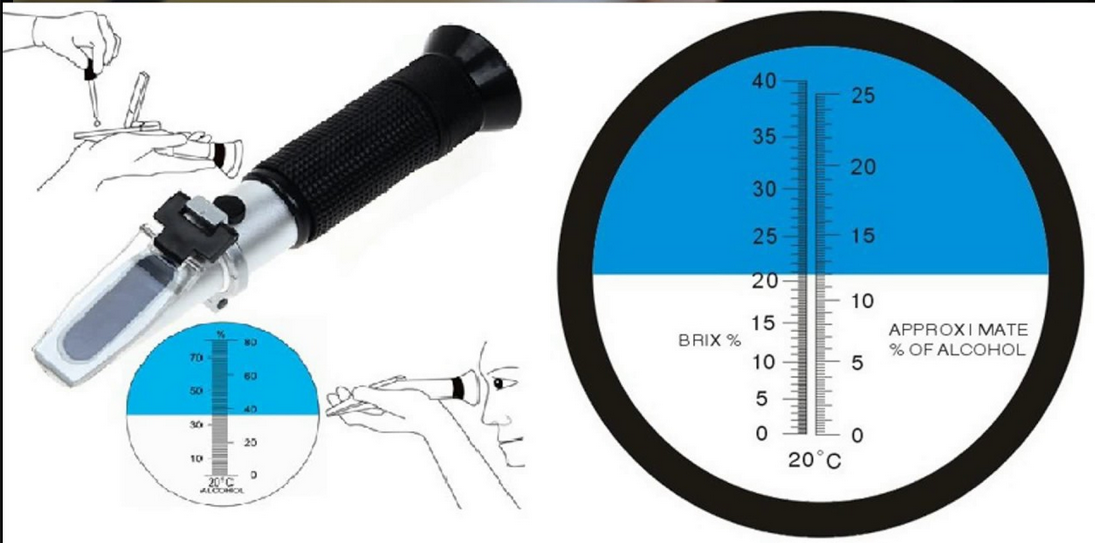


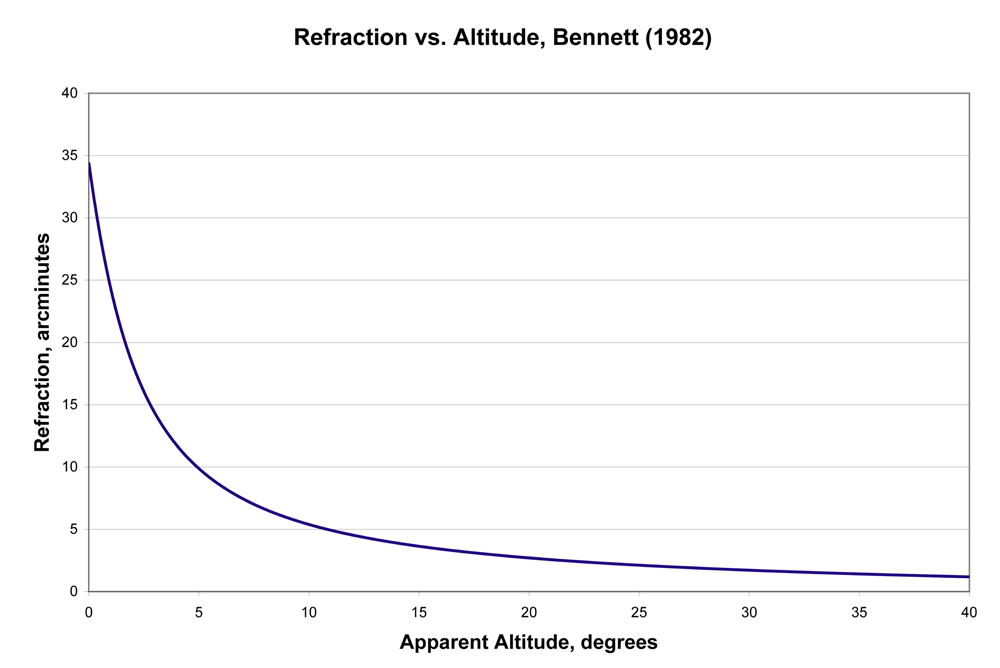
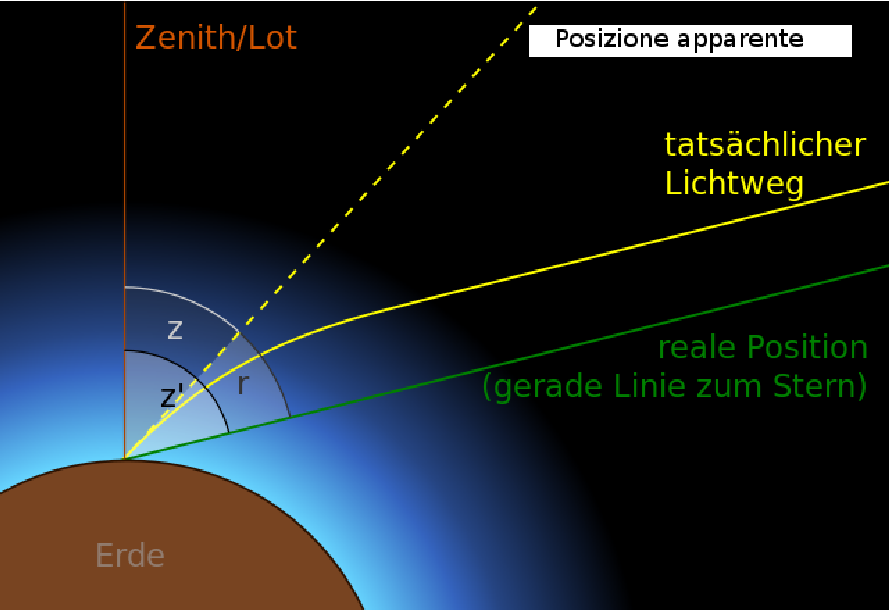





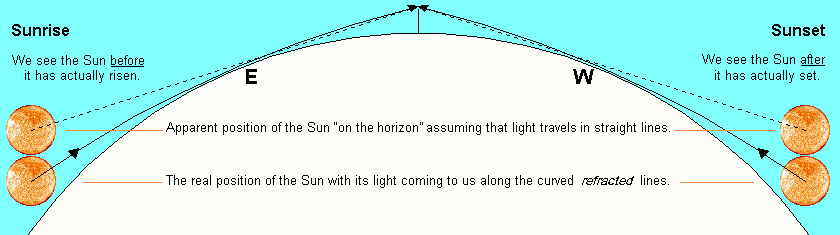
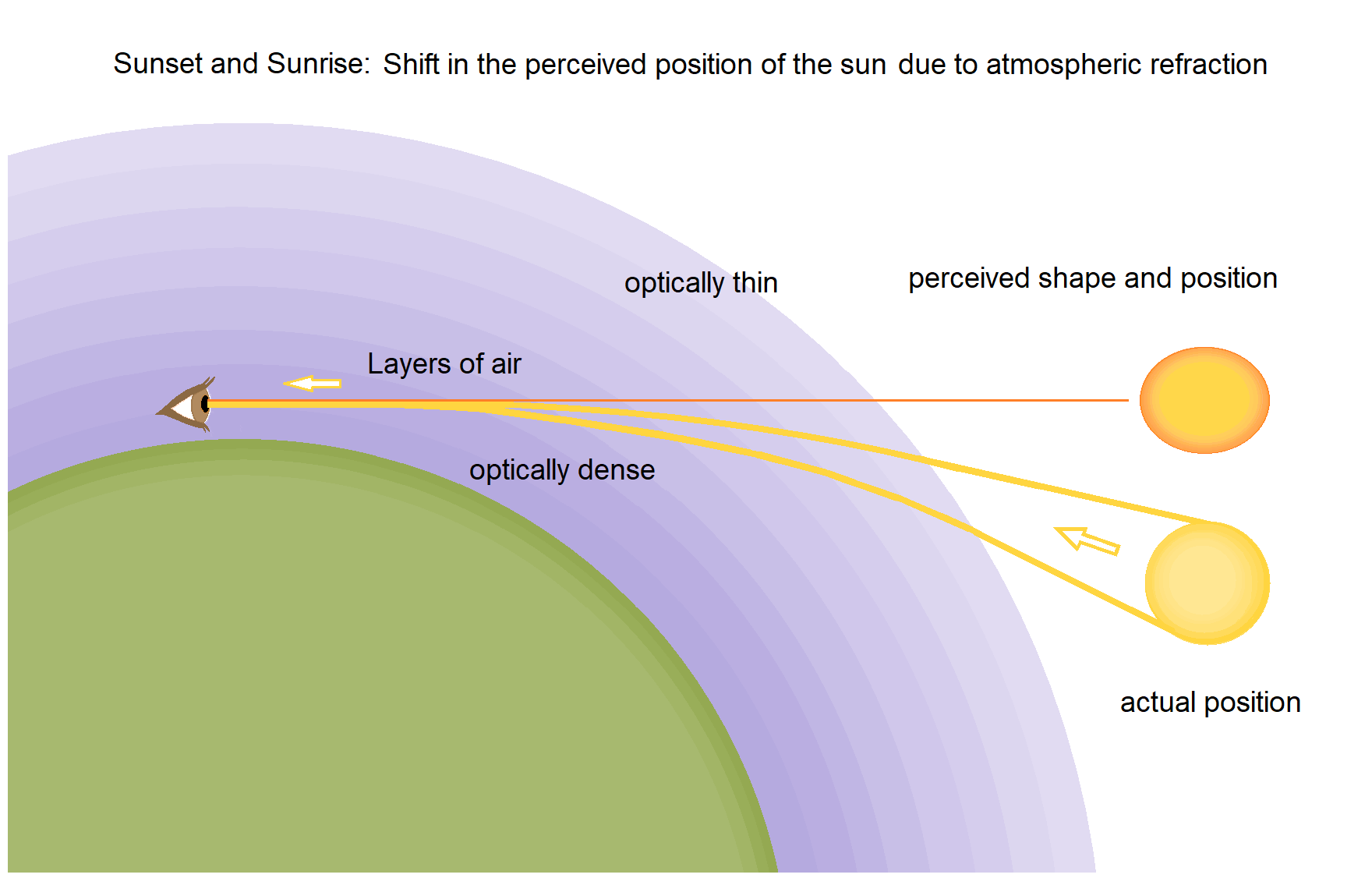
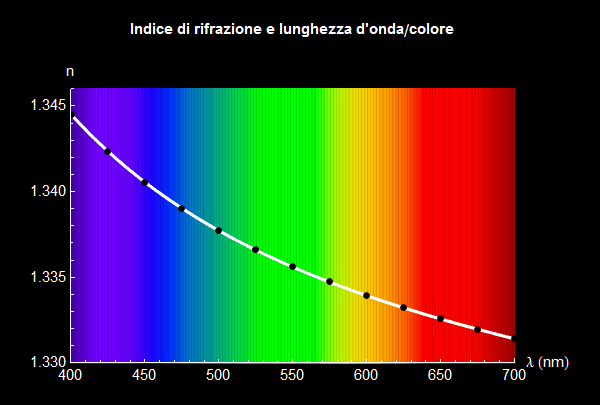



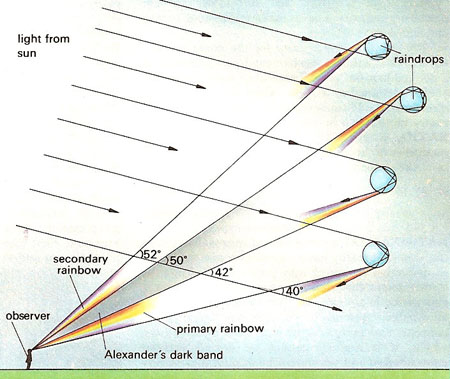



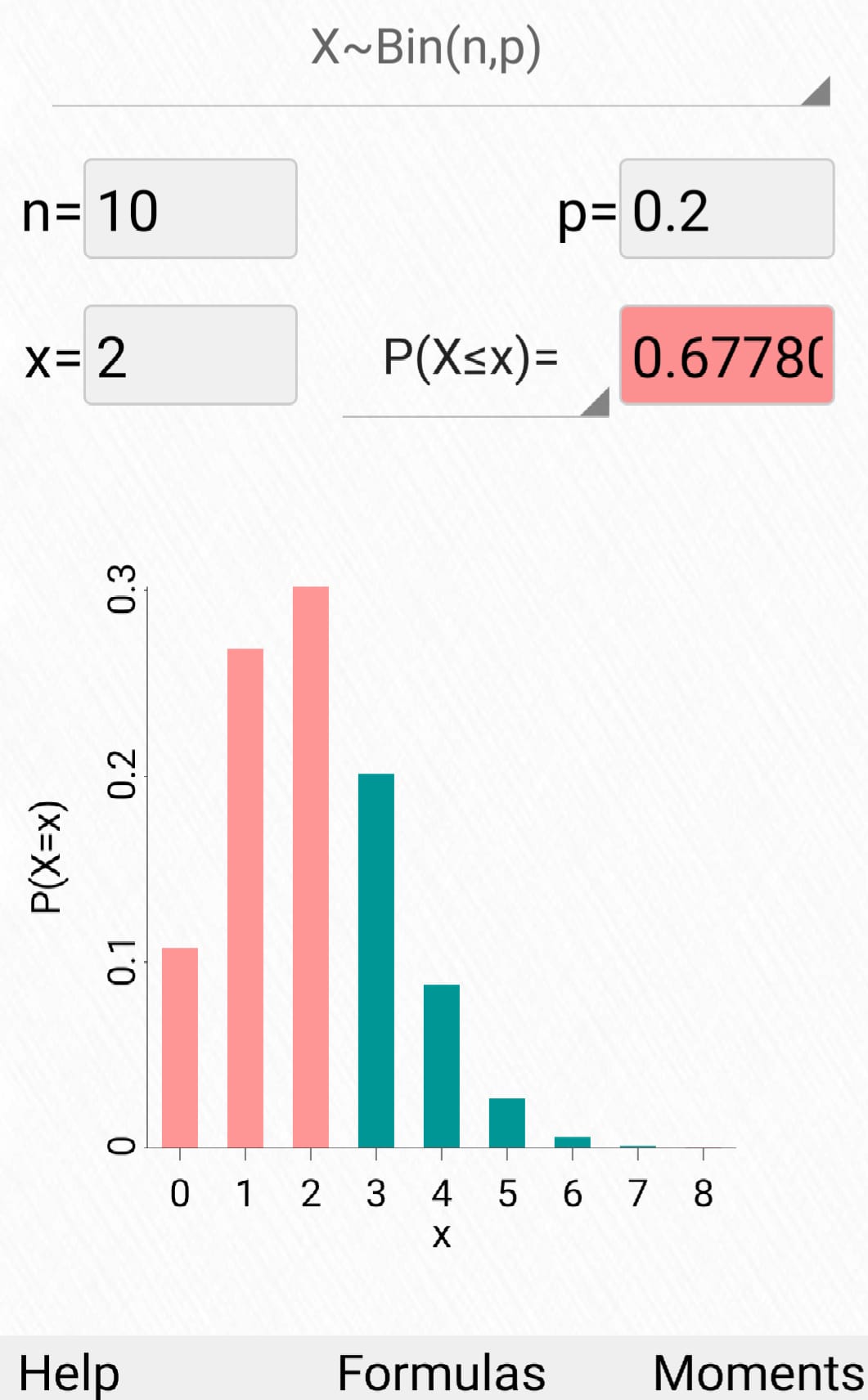
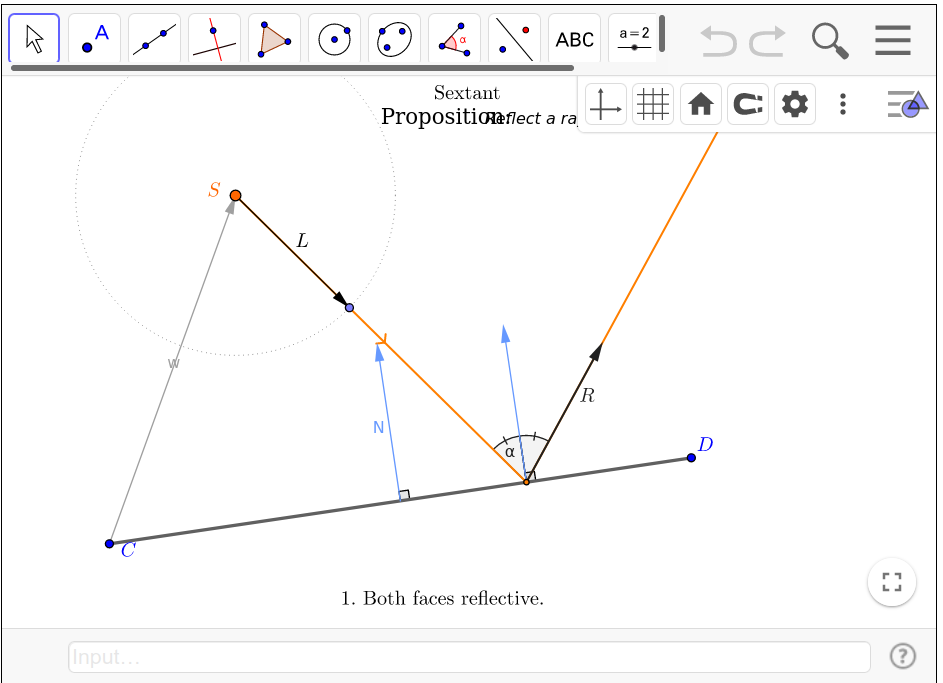



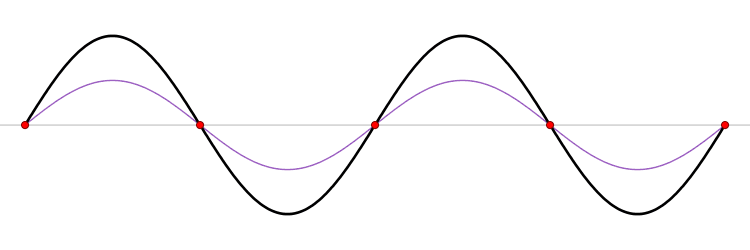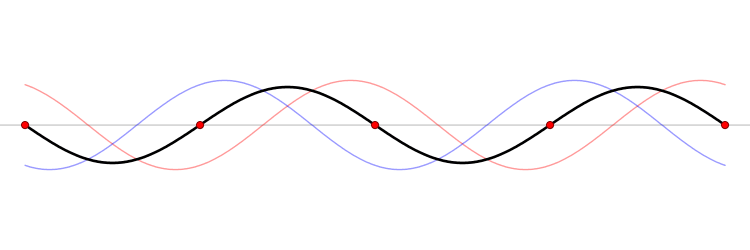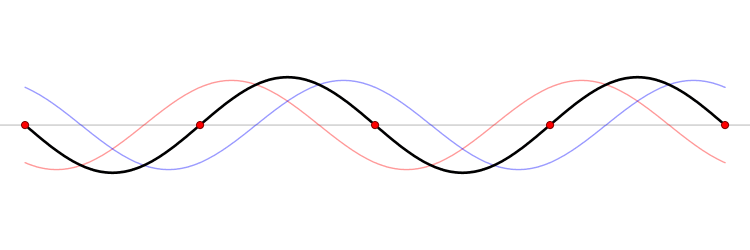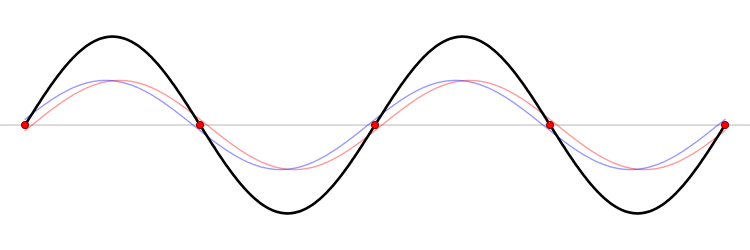
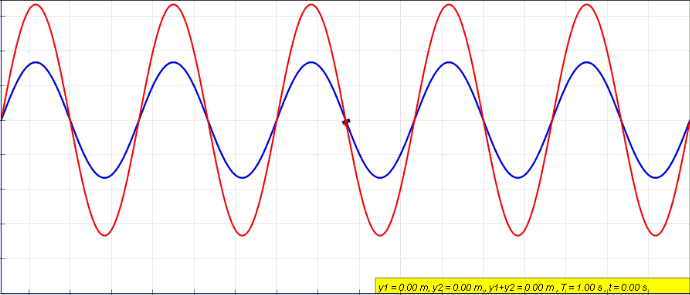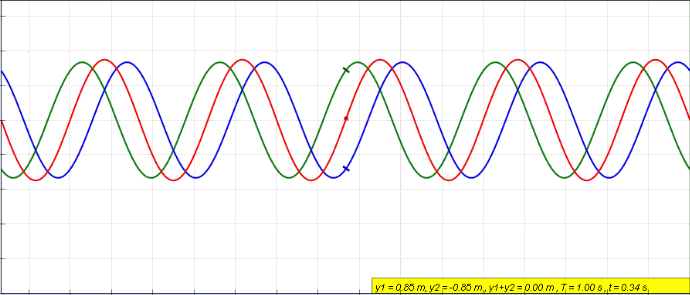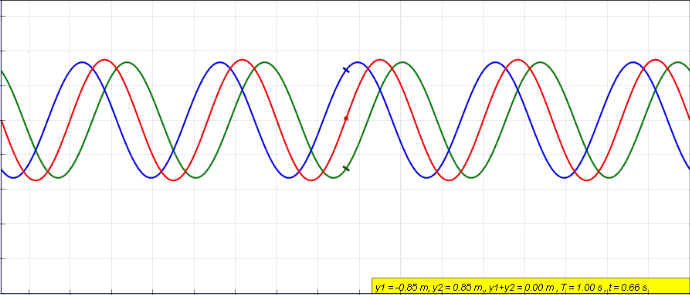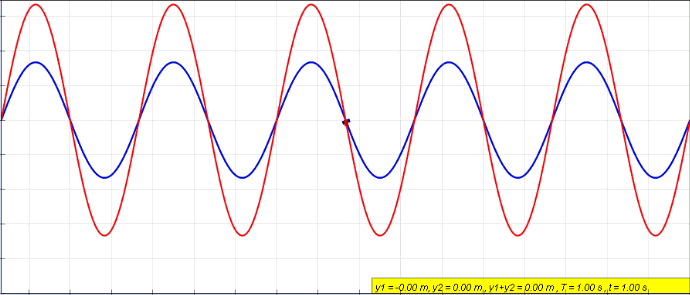
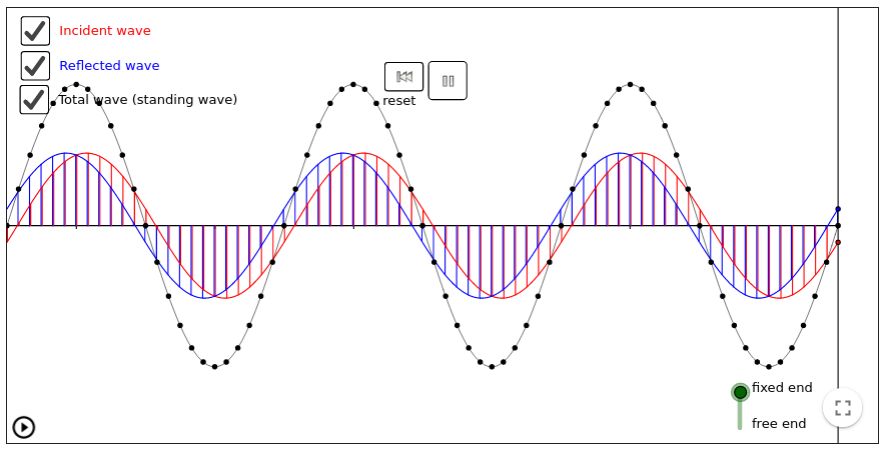
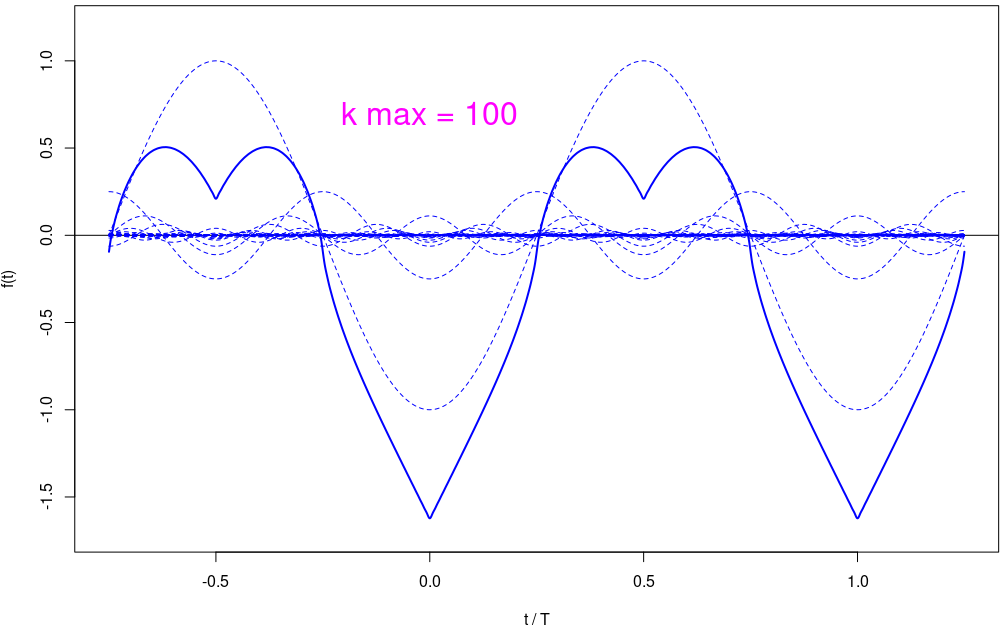
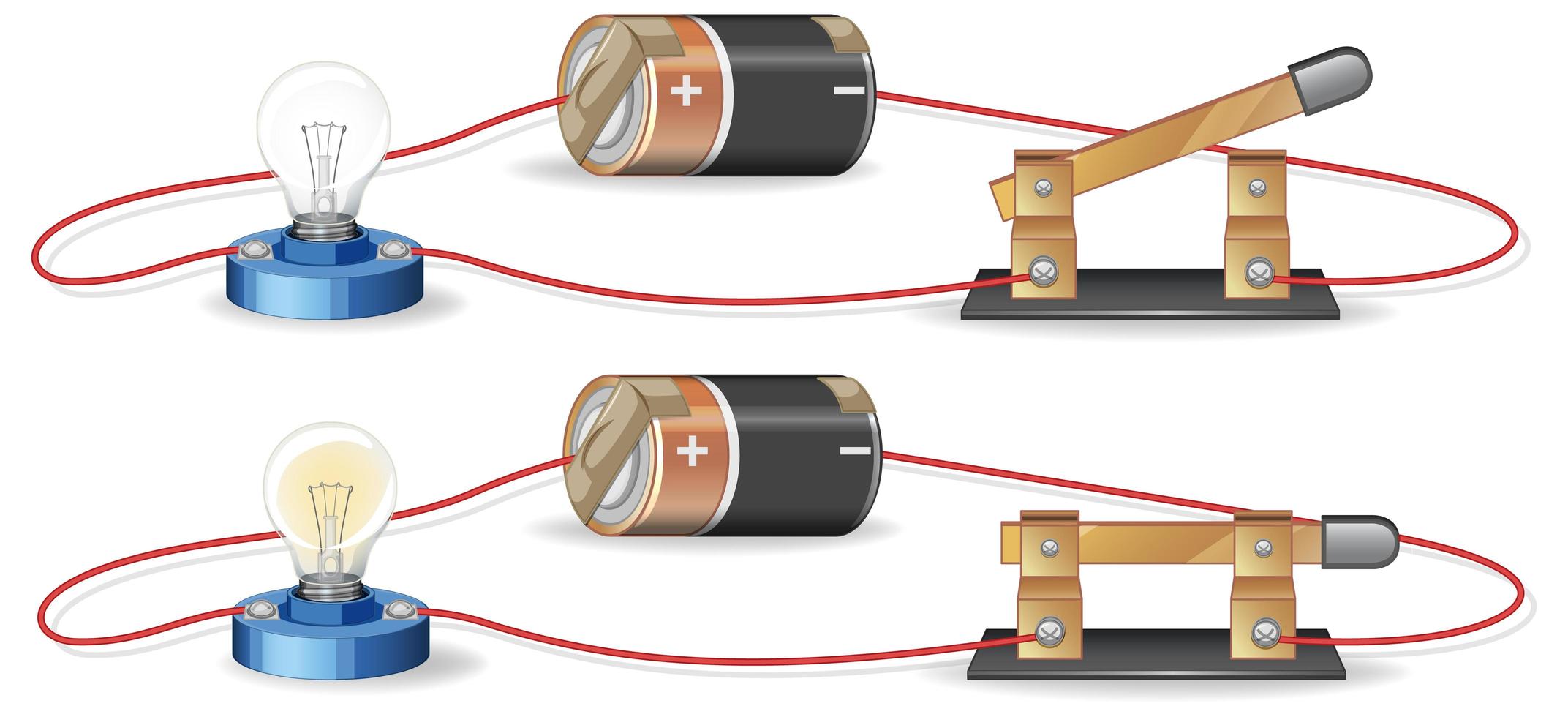
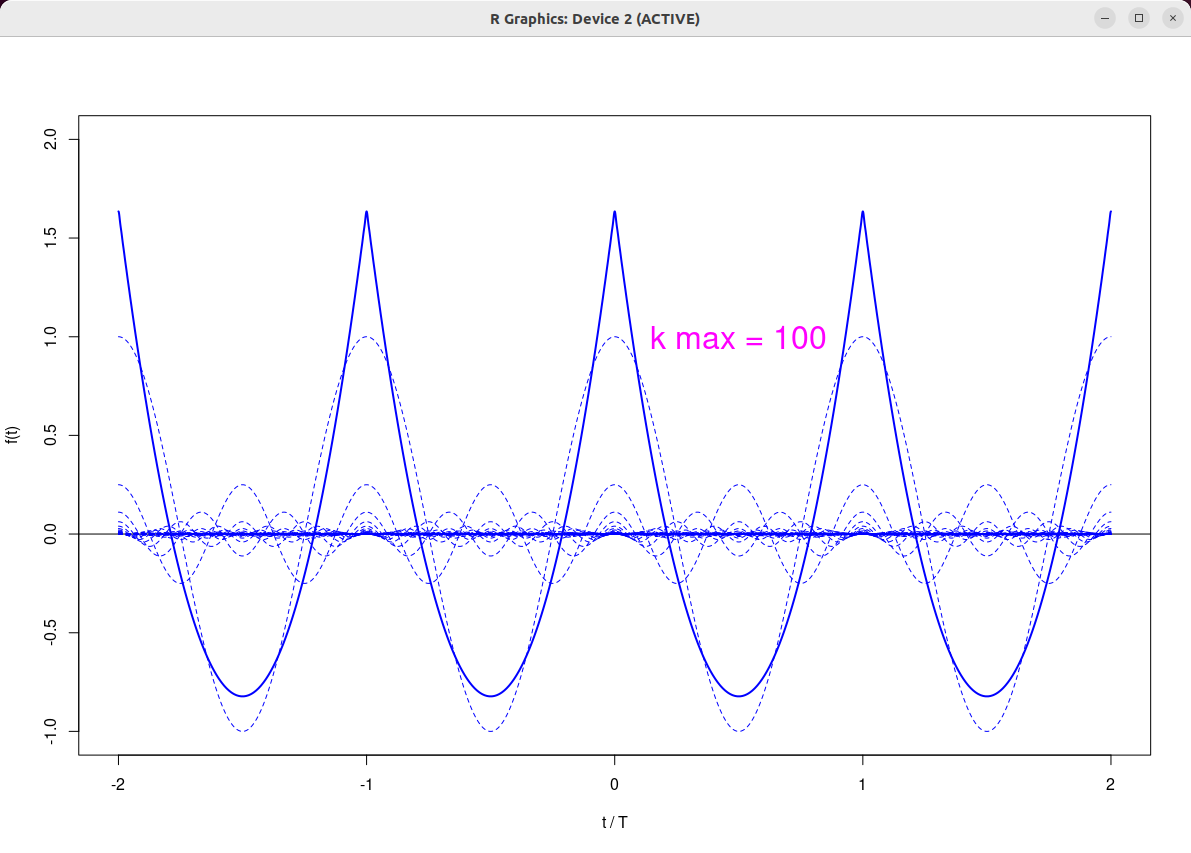
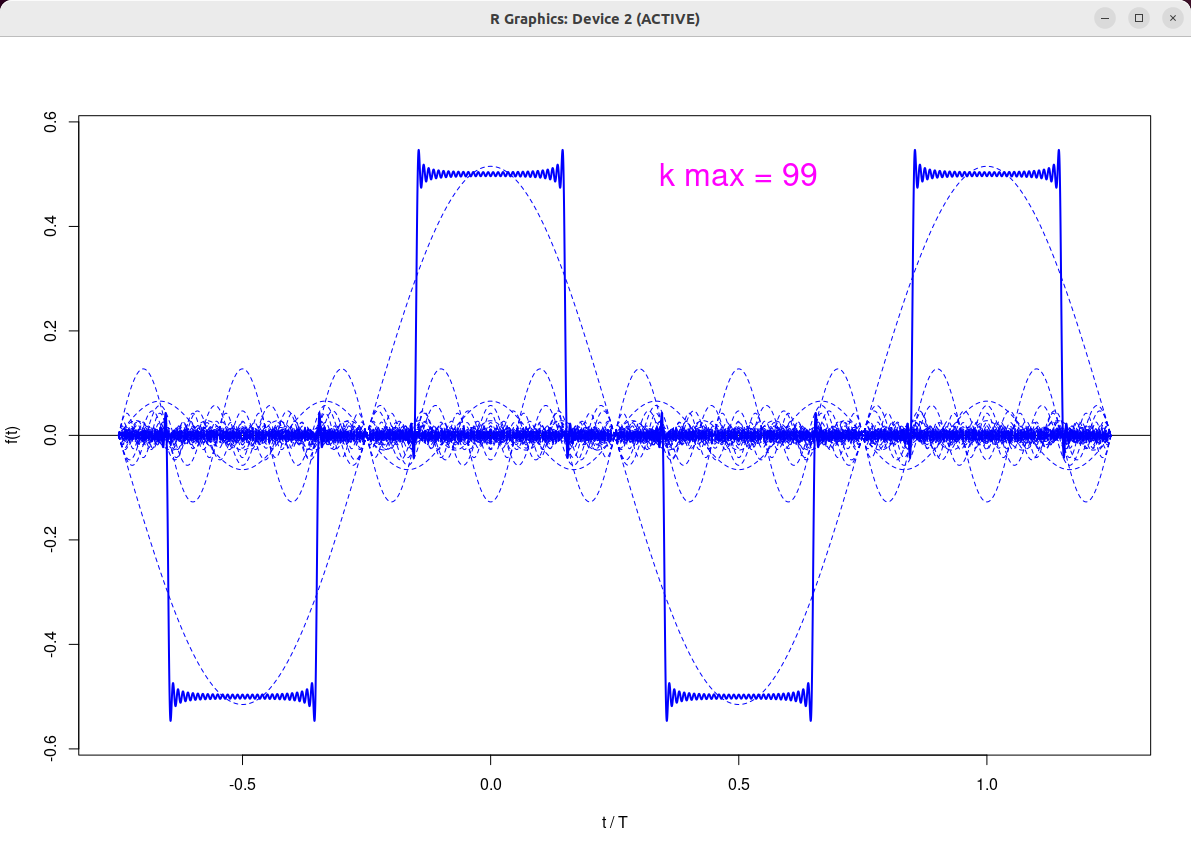
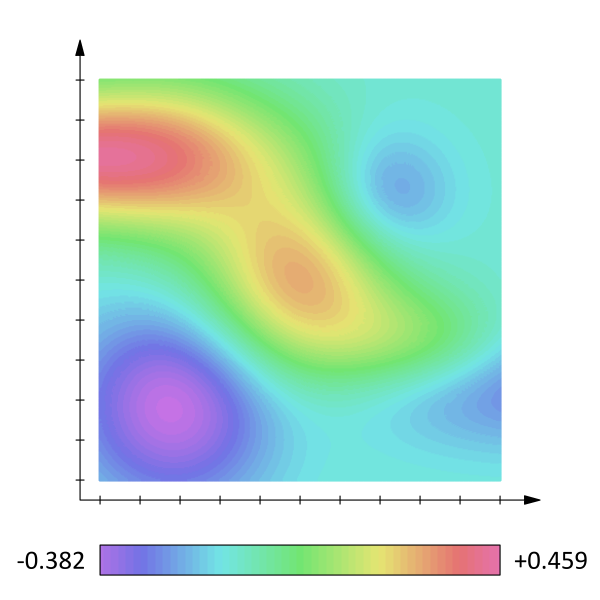

 ]
]
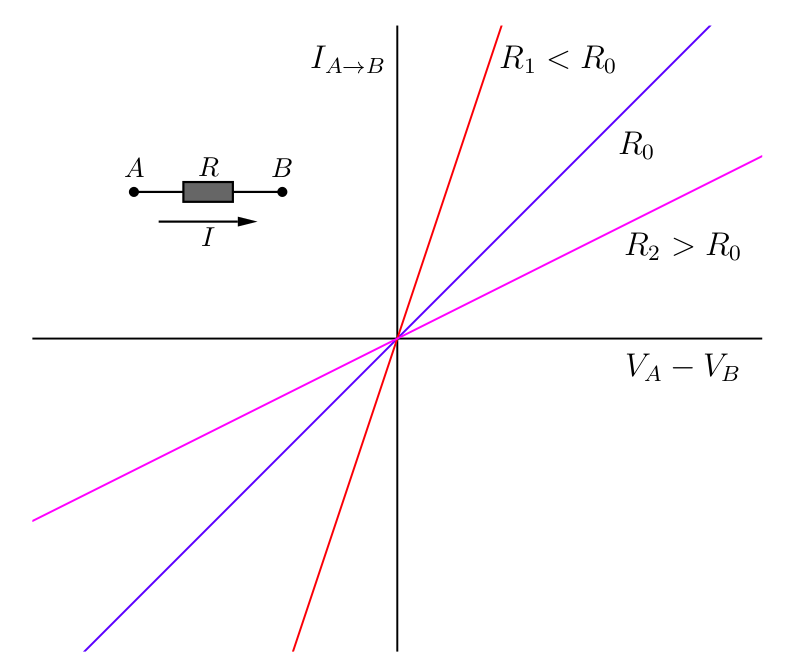
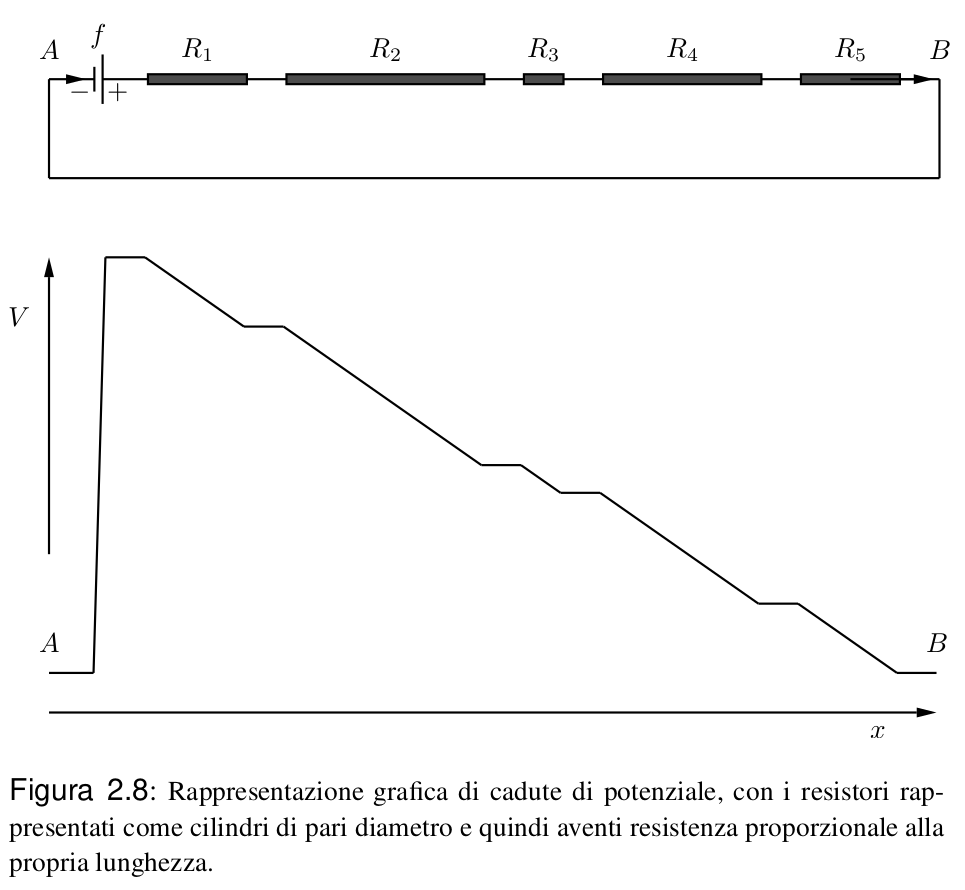
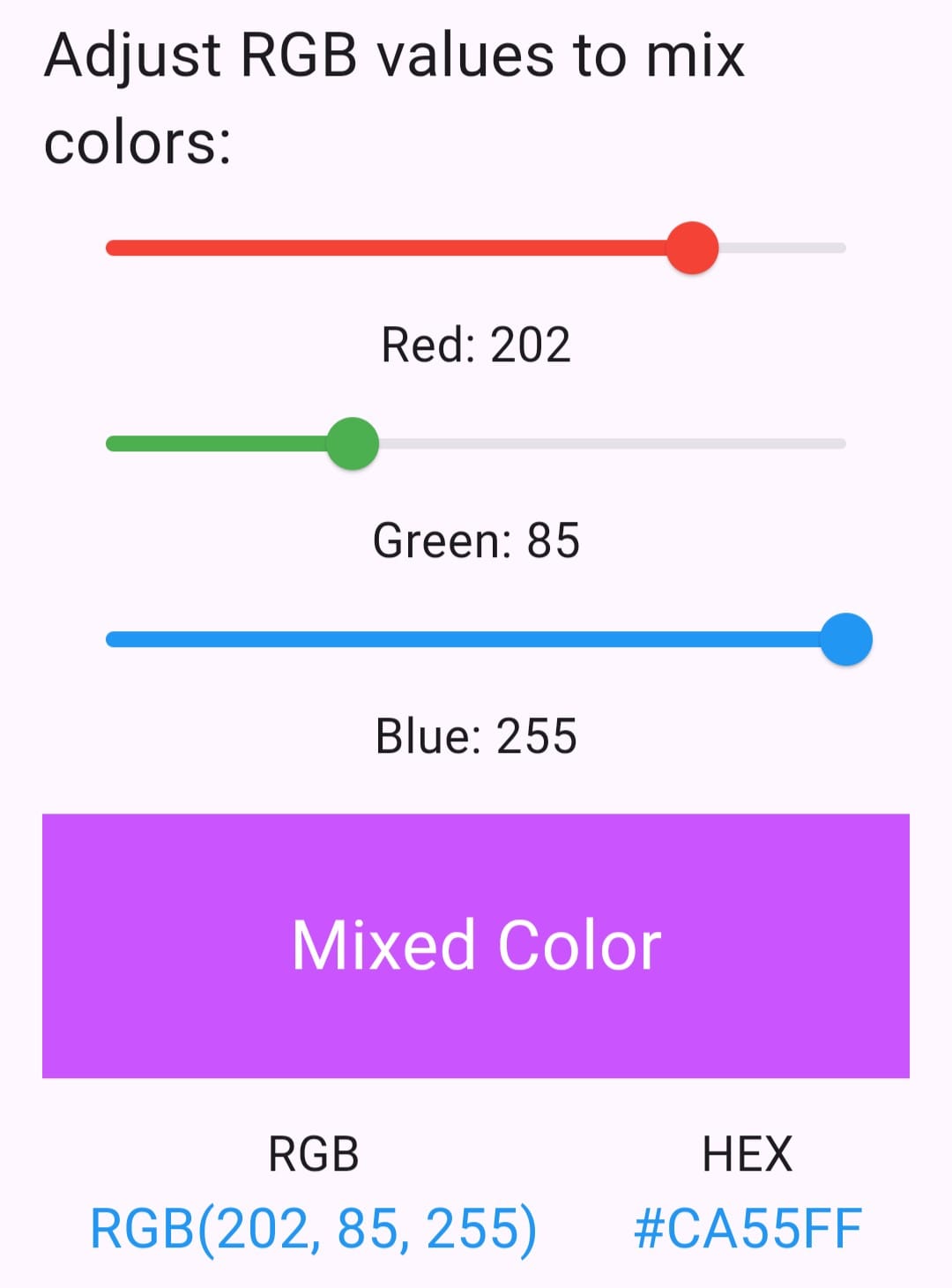
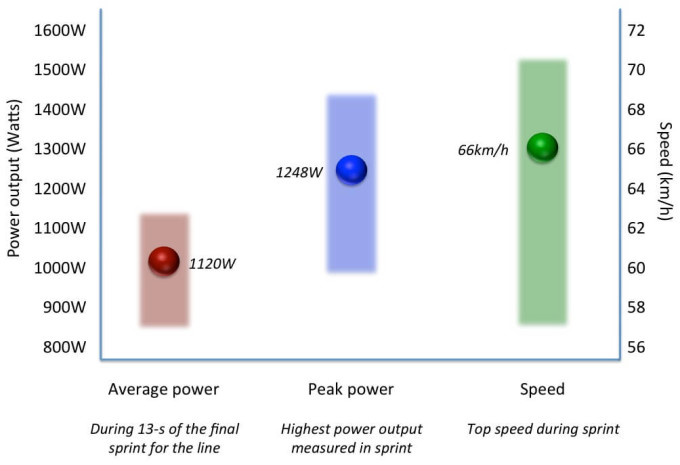
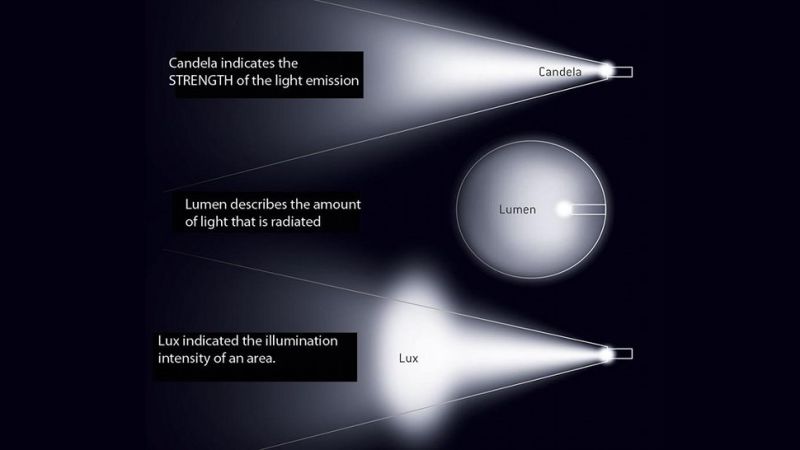
|
| |

|
|

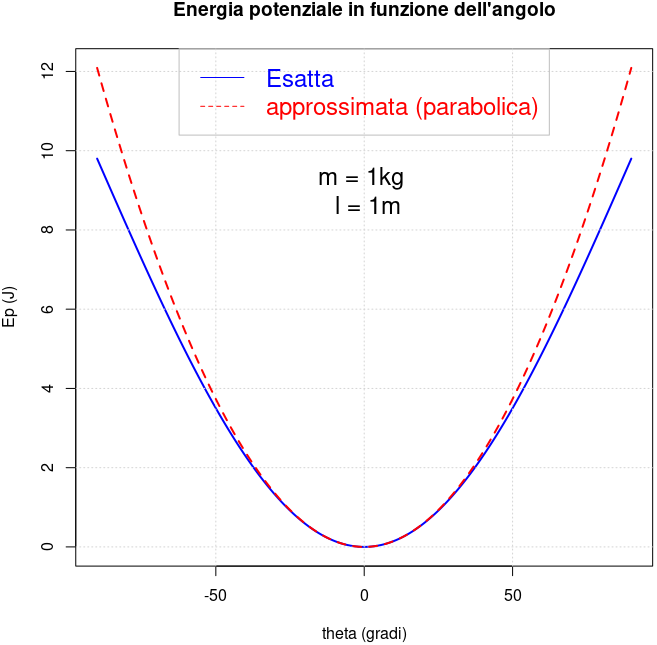
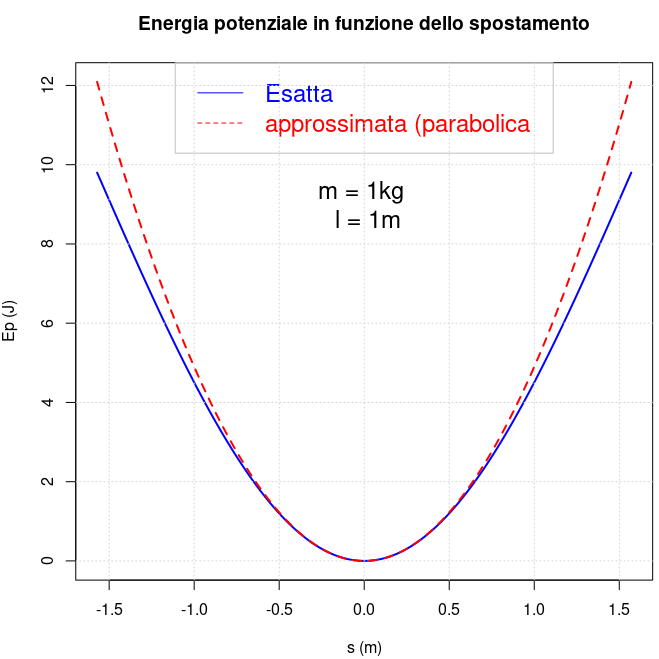
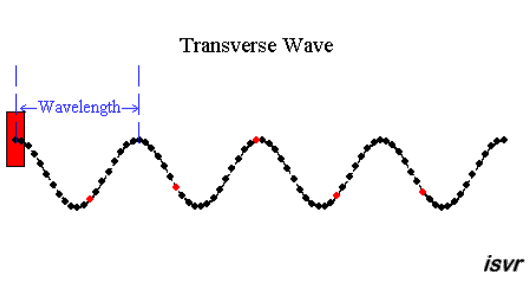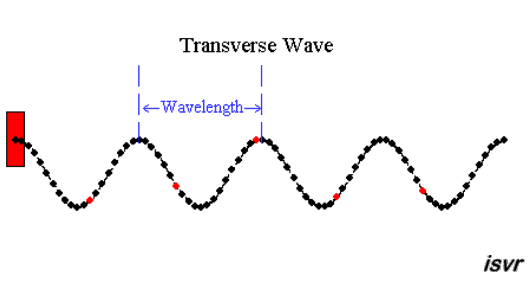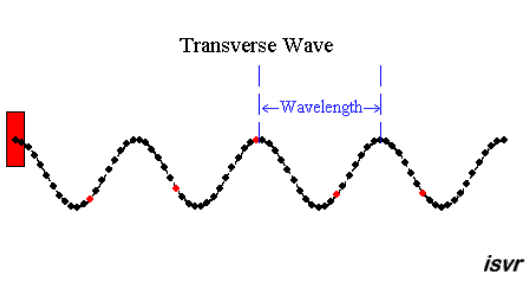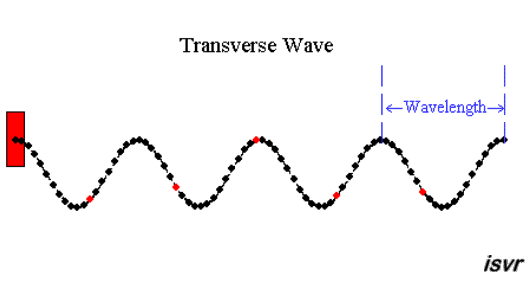
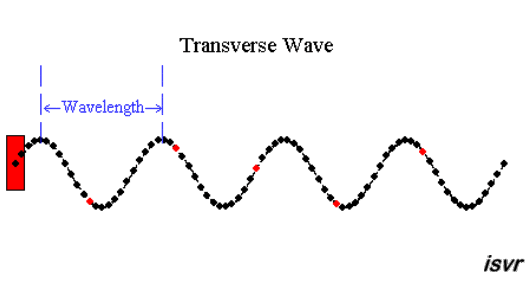
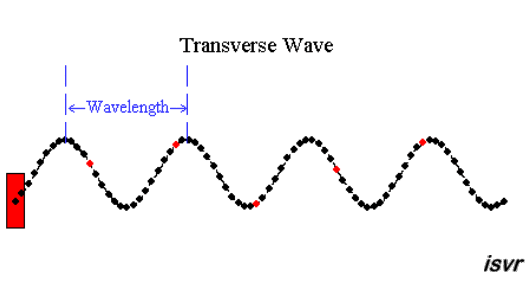
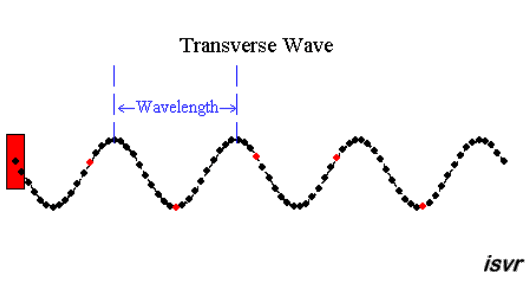
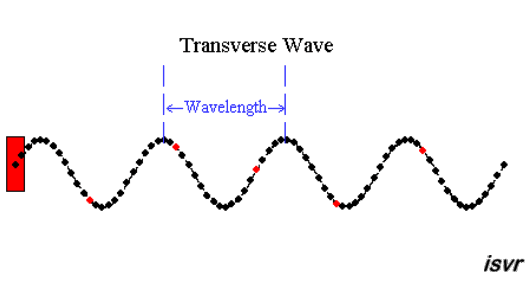
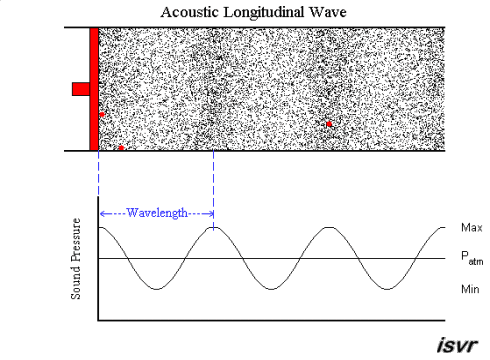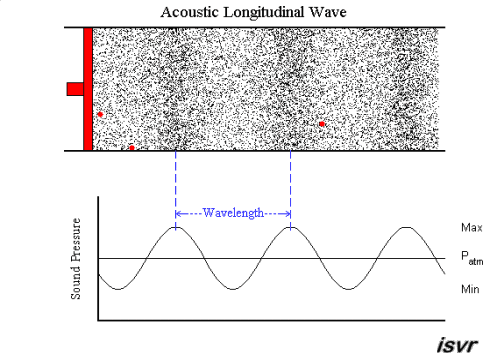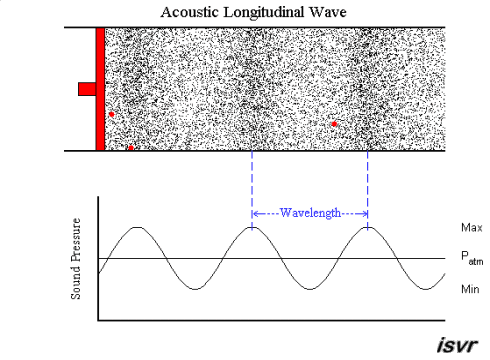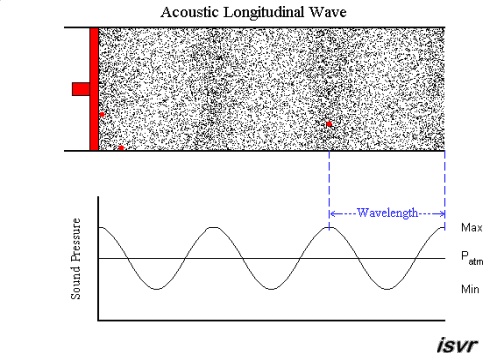

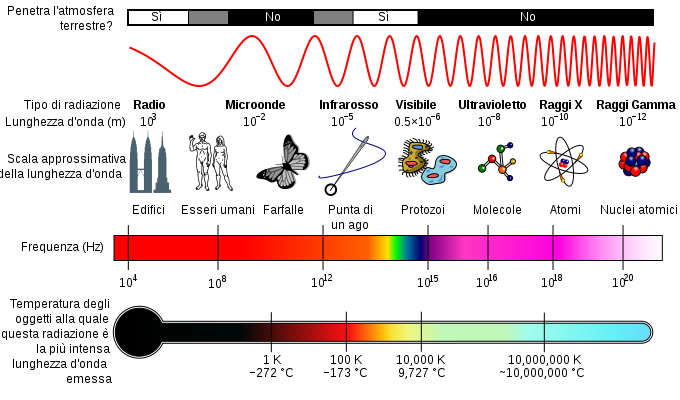
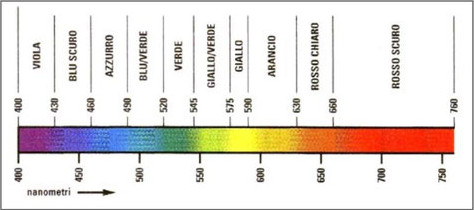






 |  | |
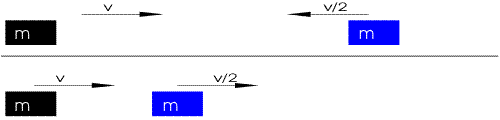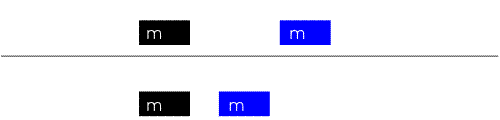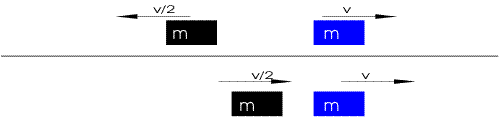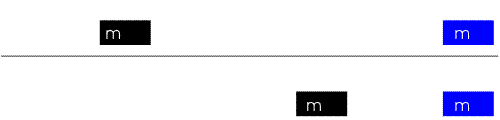
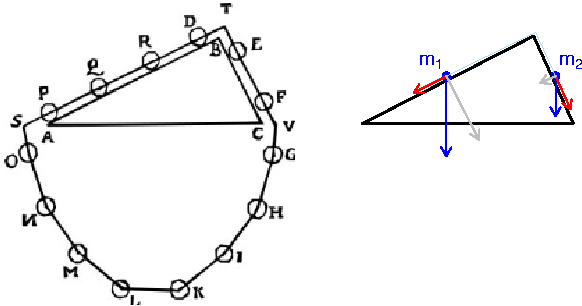
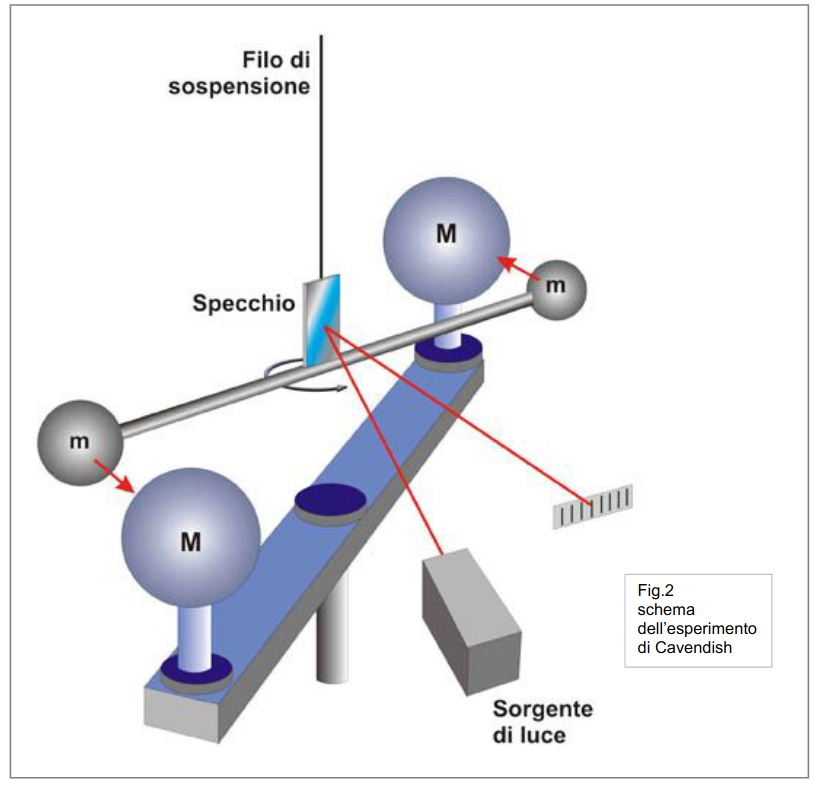
| "è un pendolo con una grande forza" | "due corpi
... si respingono con forze che sono proporzionali alla forza che avevano quando si sono incontrati" |







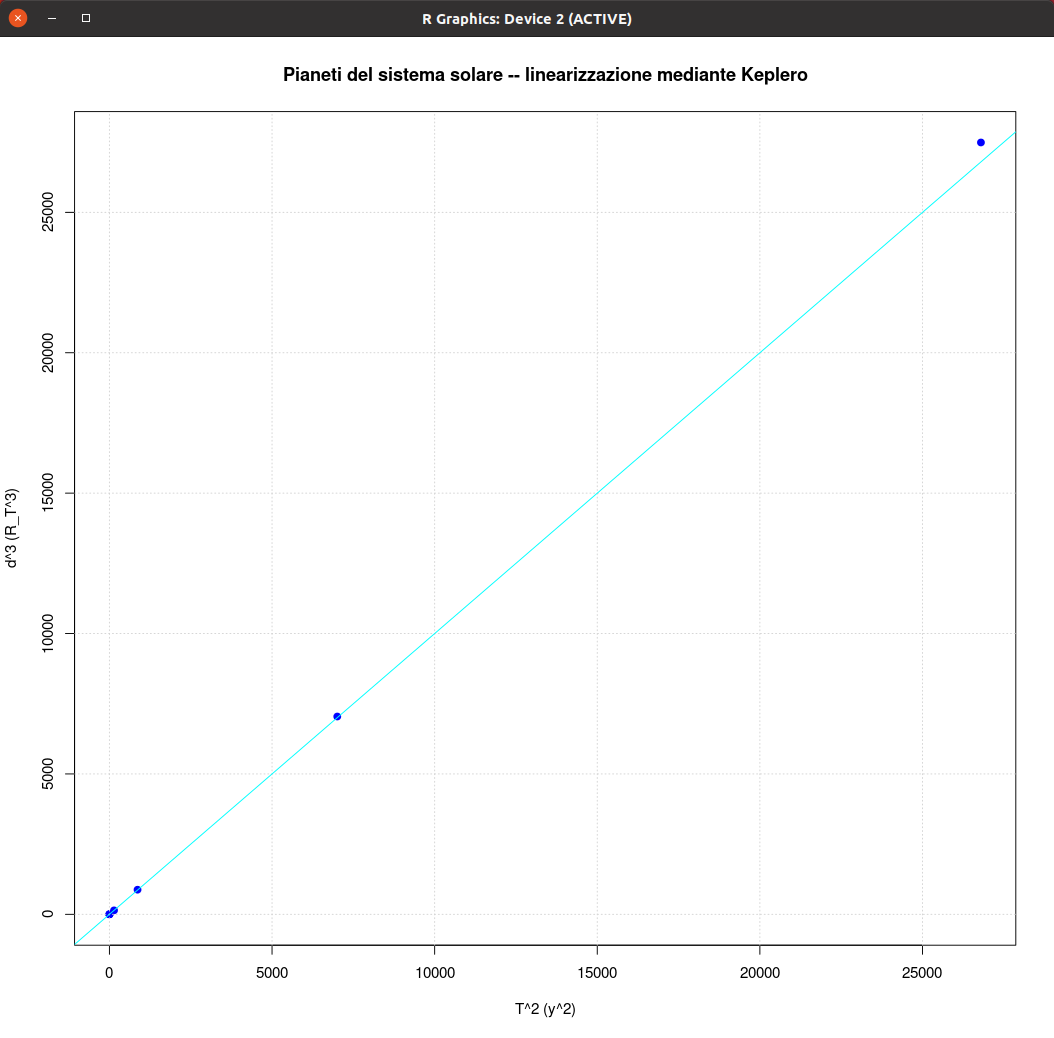
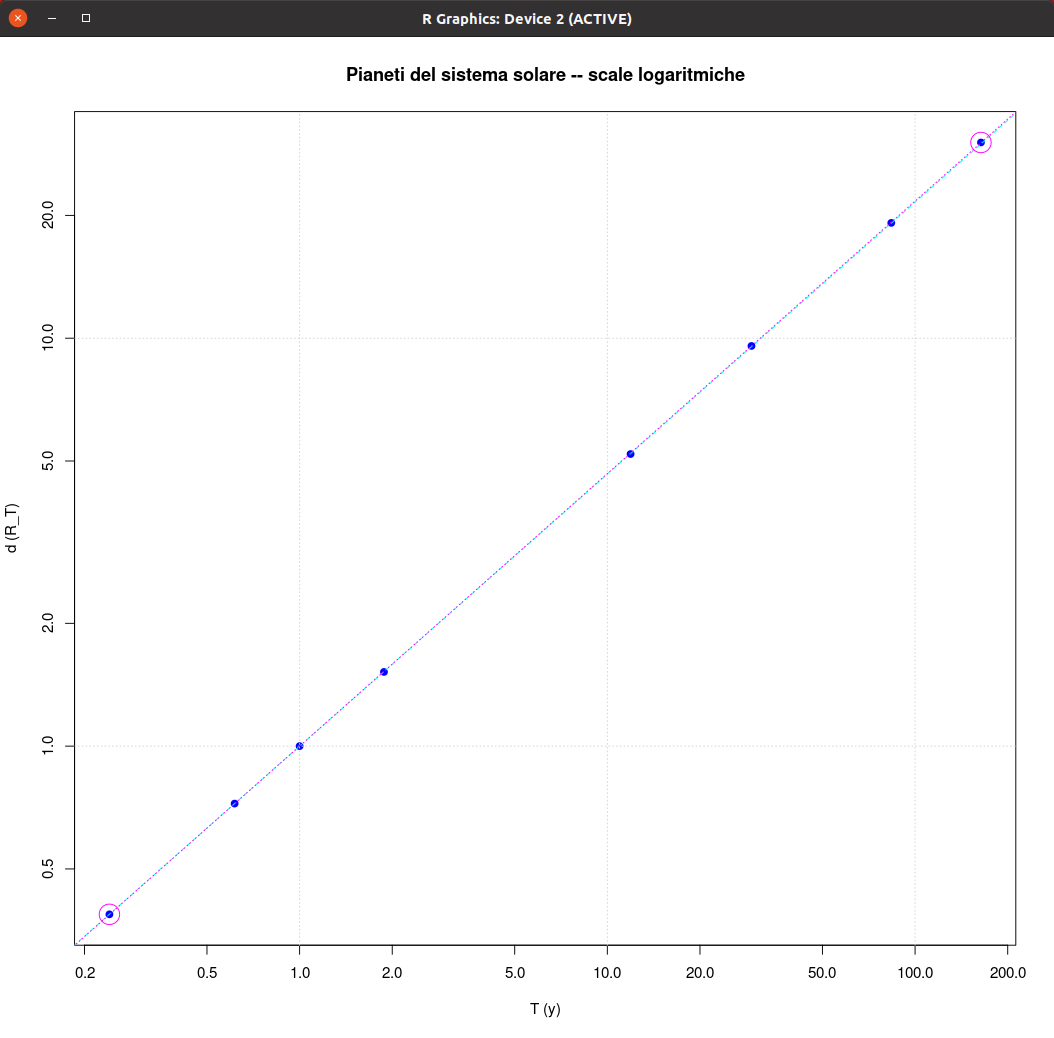
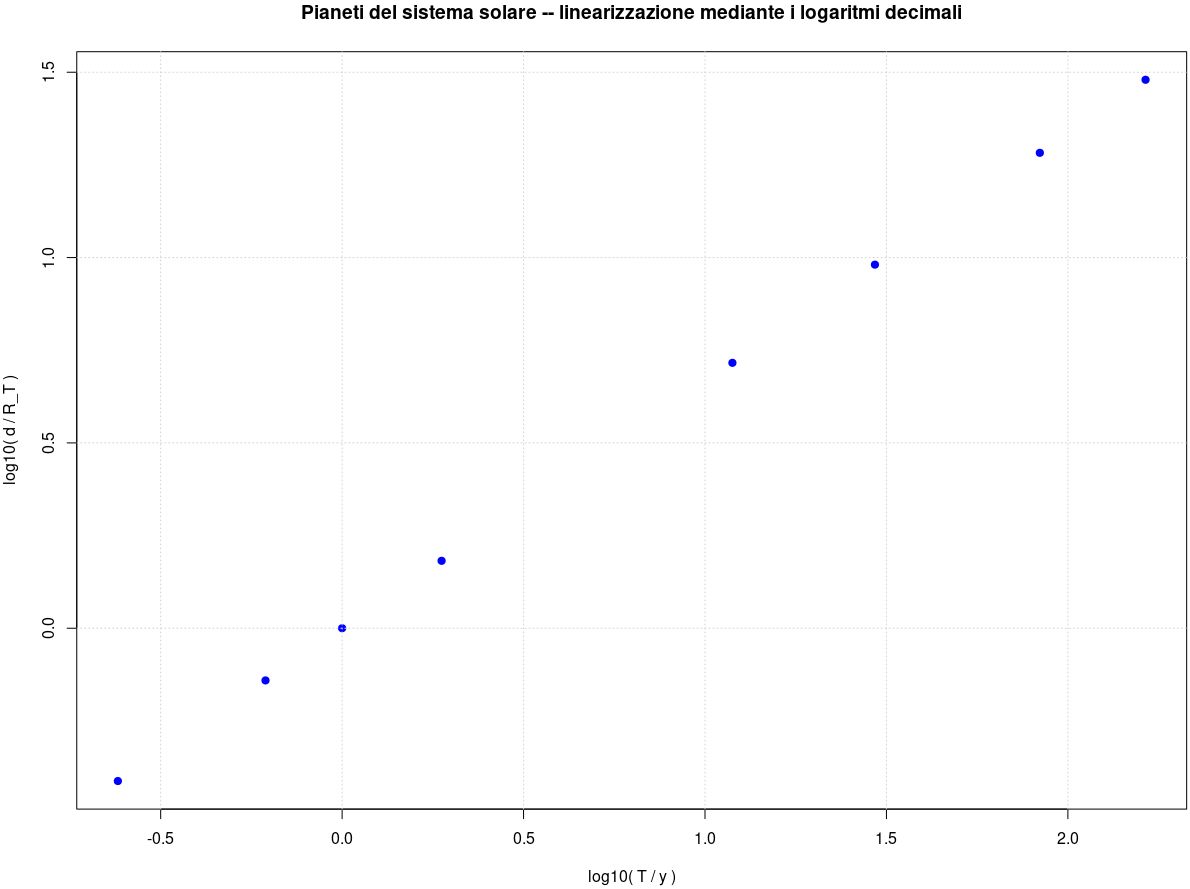
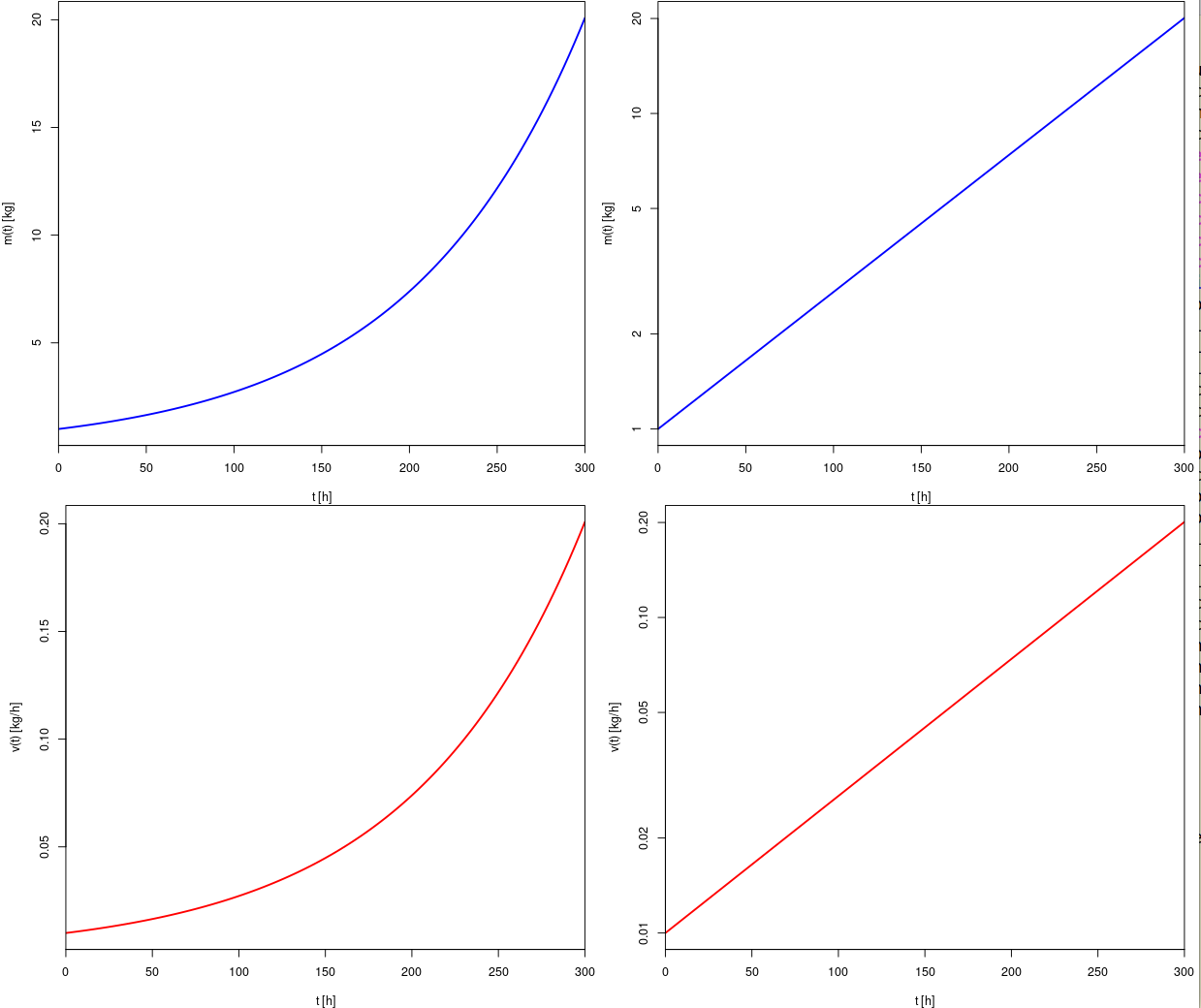
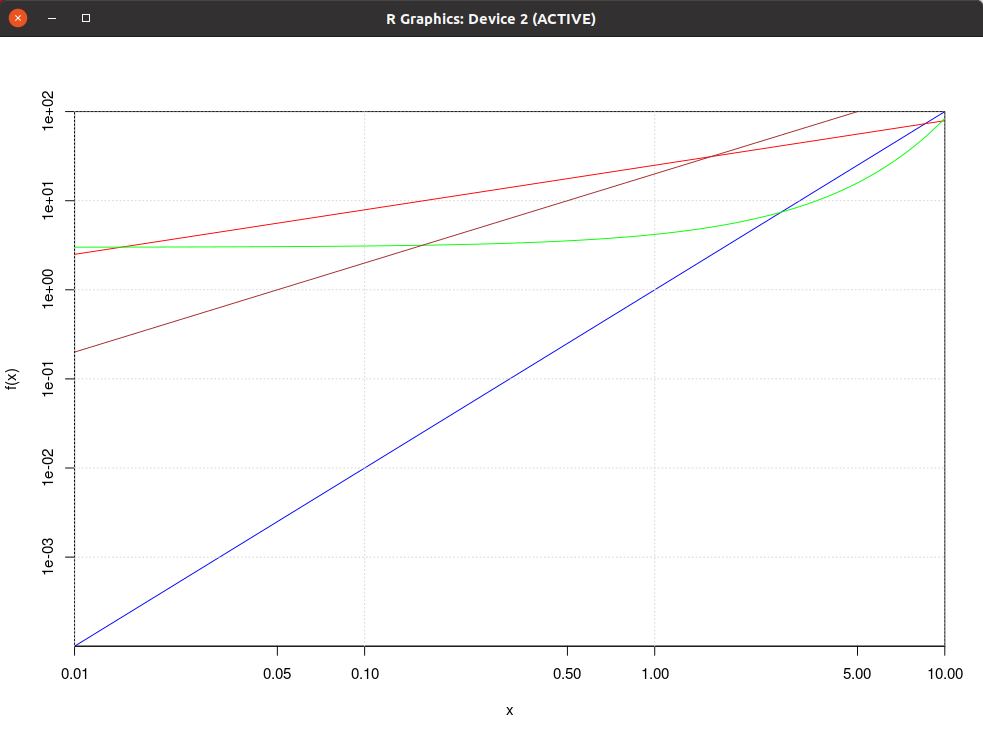
| GFLOPS |
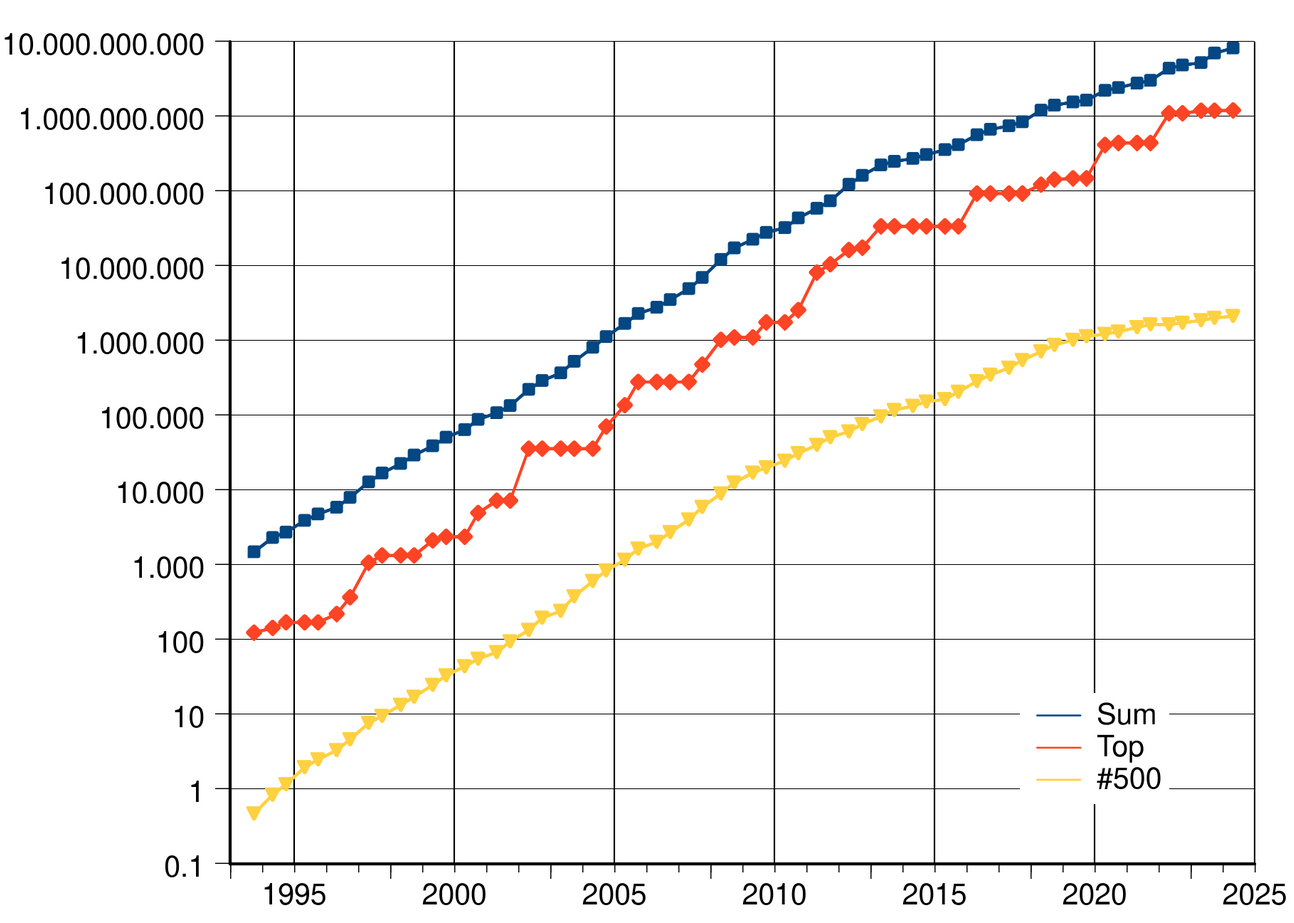
[ Trend dei sistemi operativi usati nei TOP500 ] |
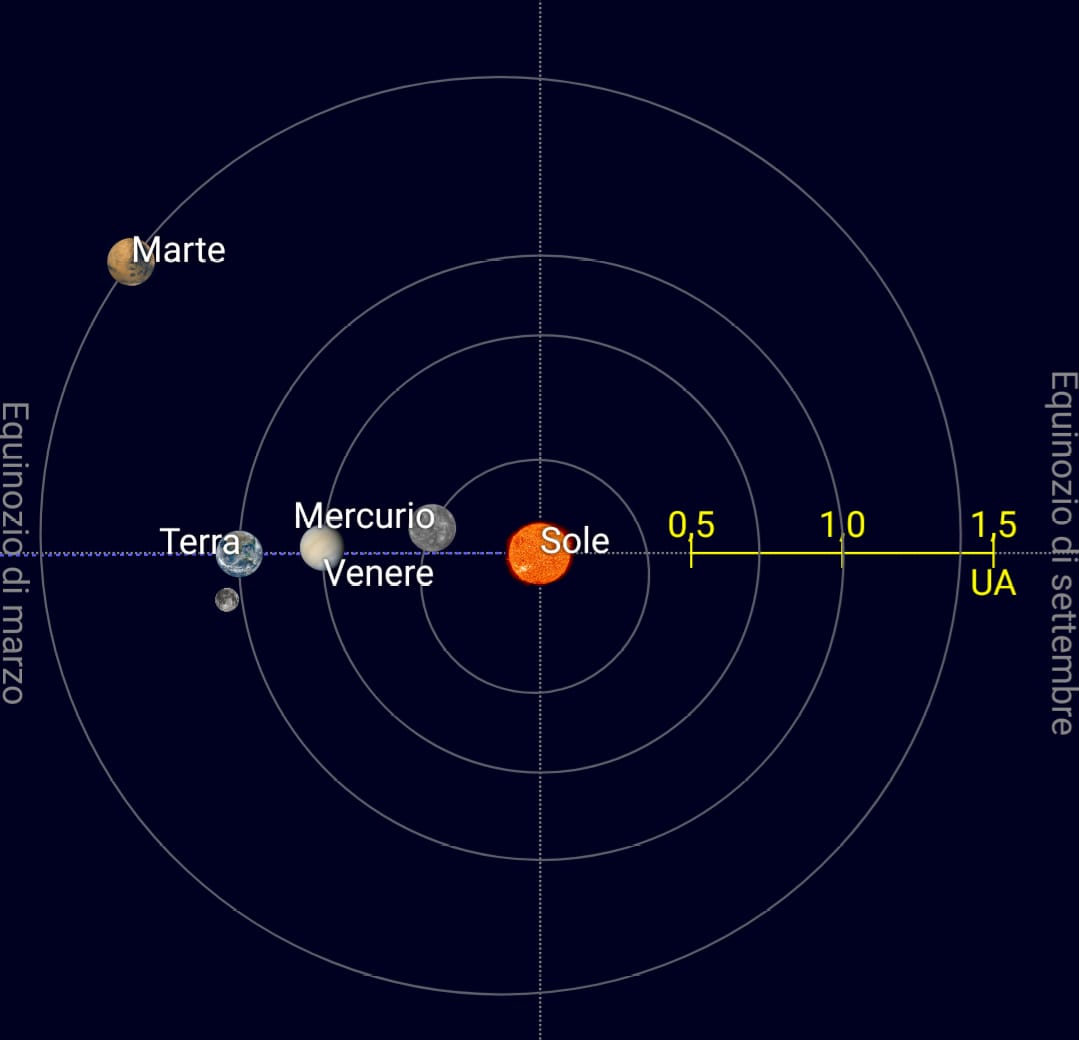

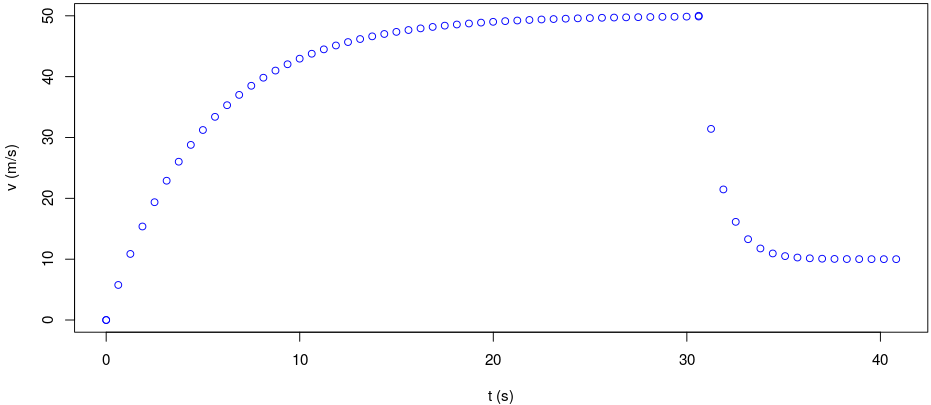




 |
 |
 |
 |
 |
 |
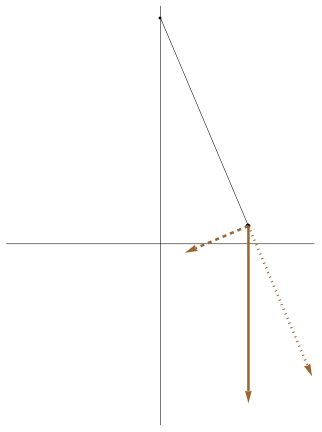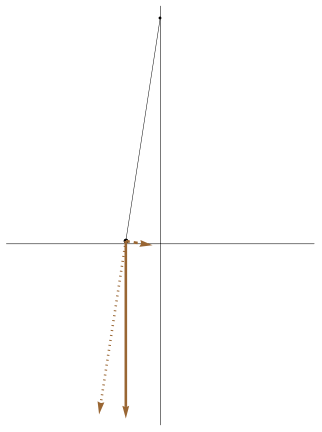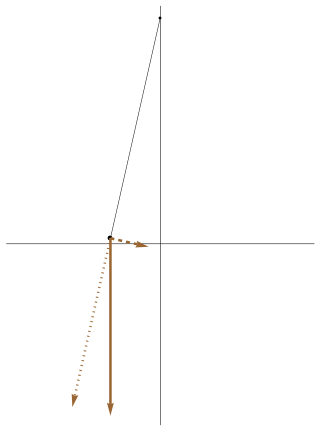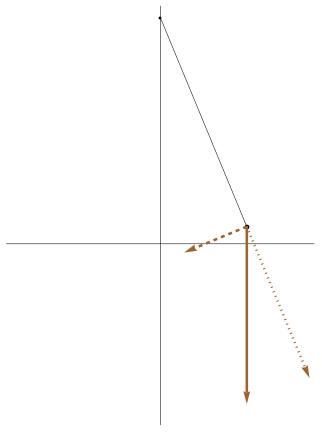
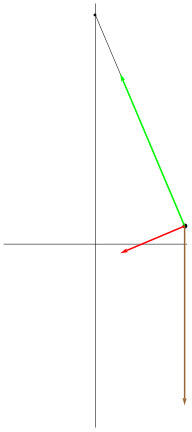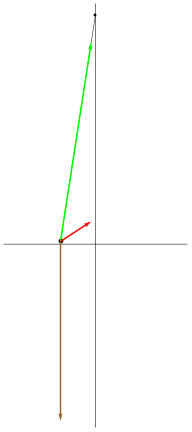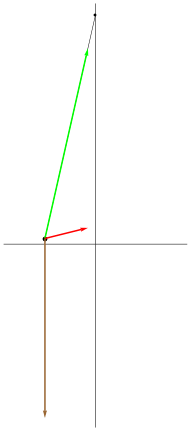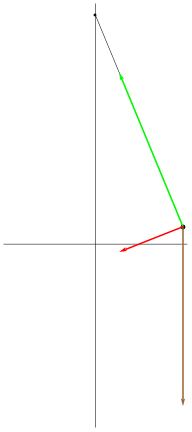
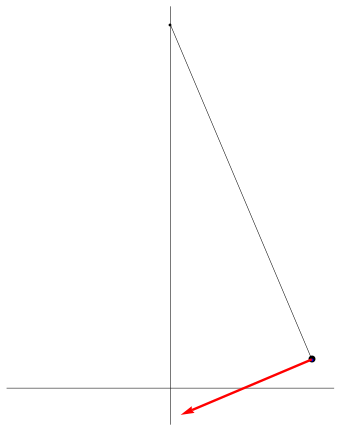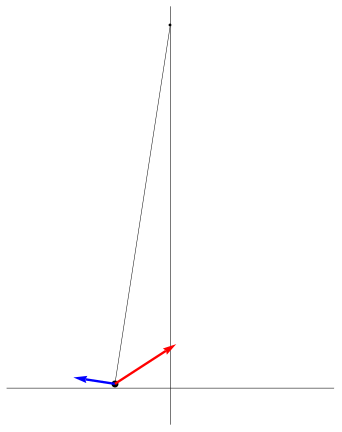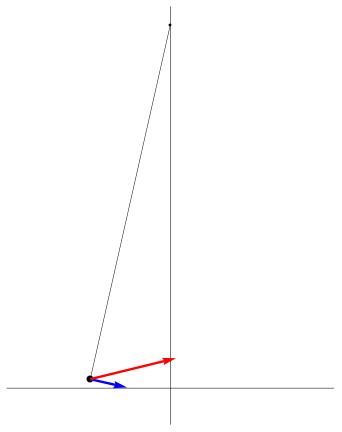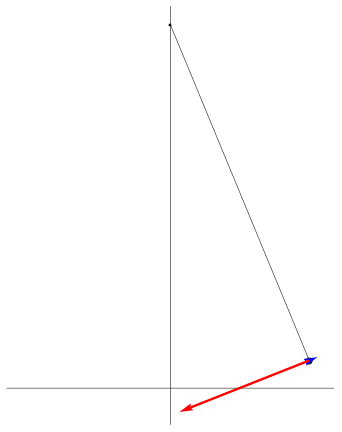












 |
 |
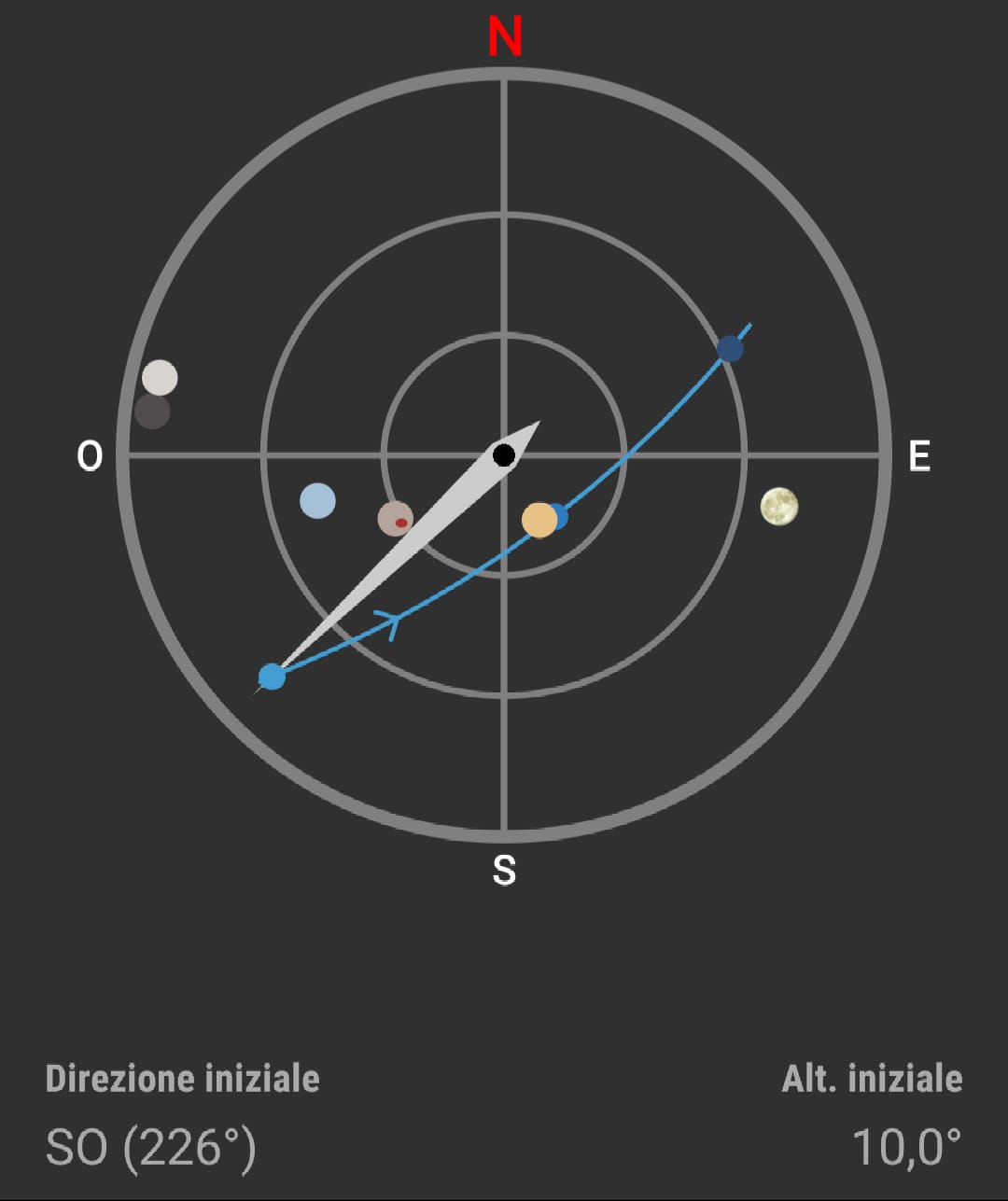
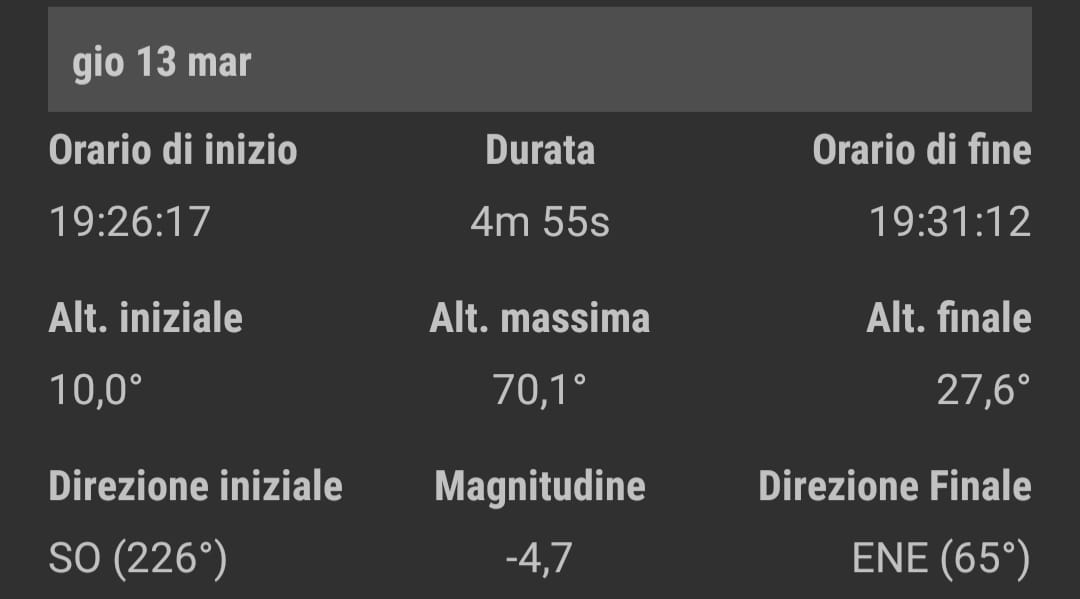
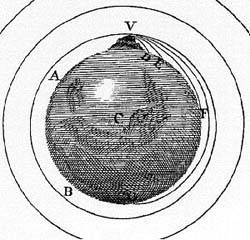
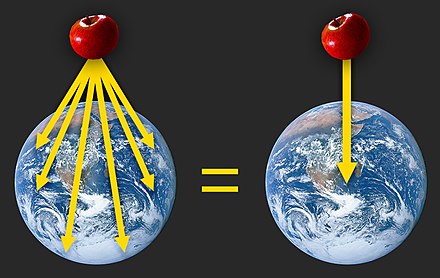
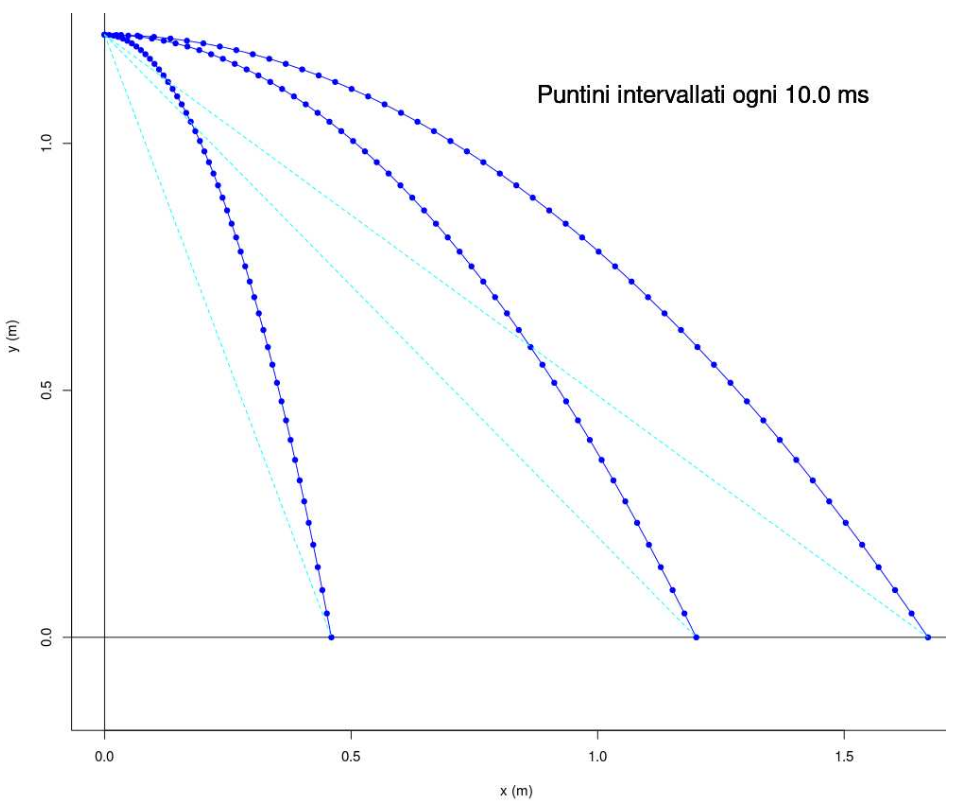
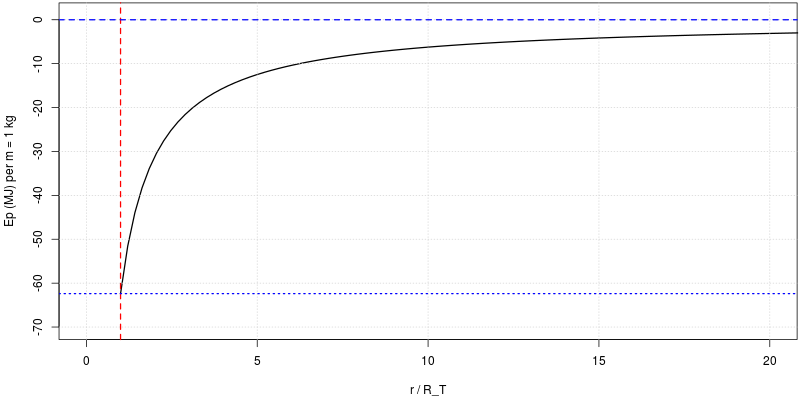
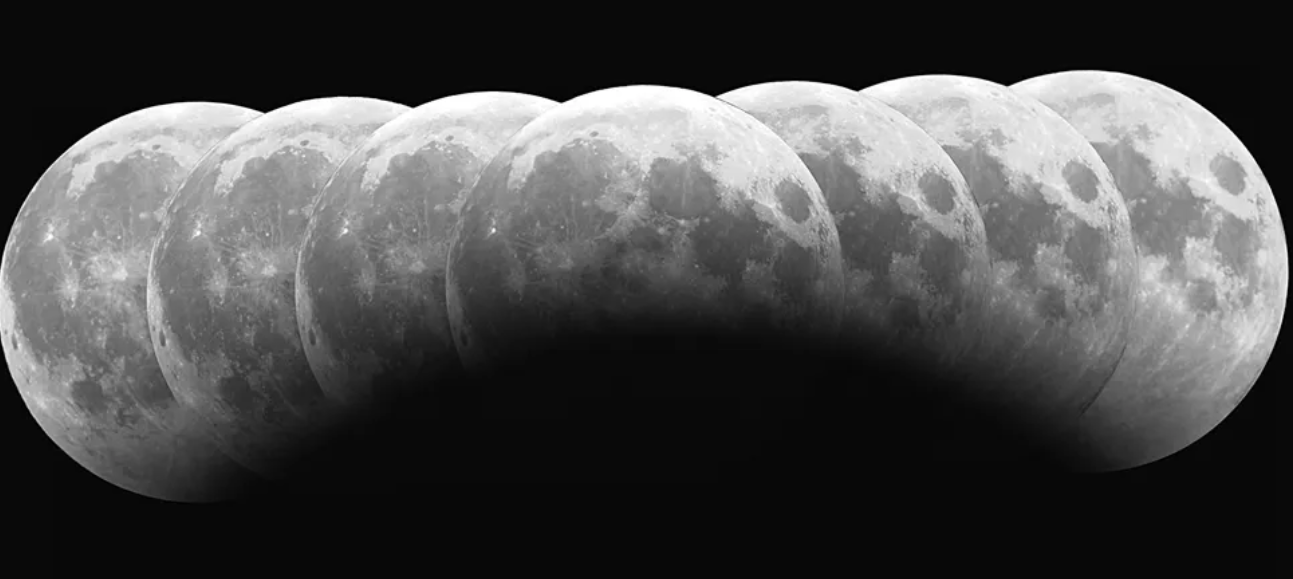
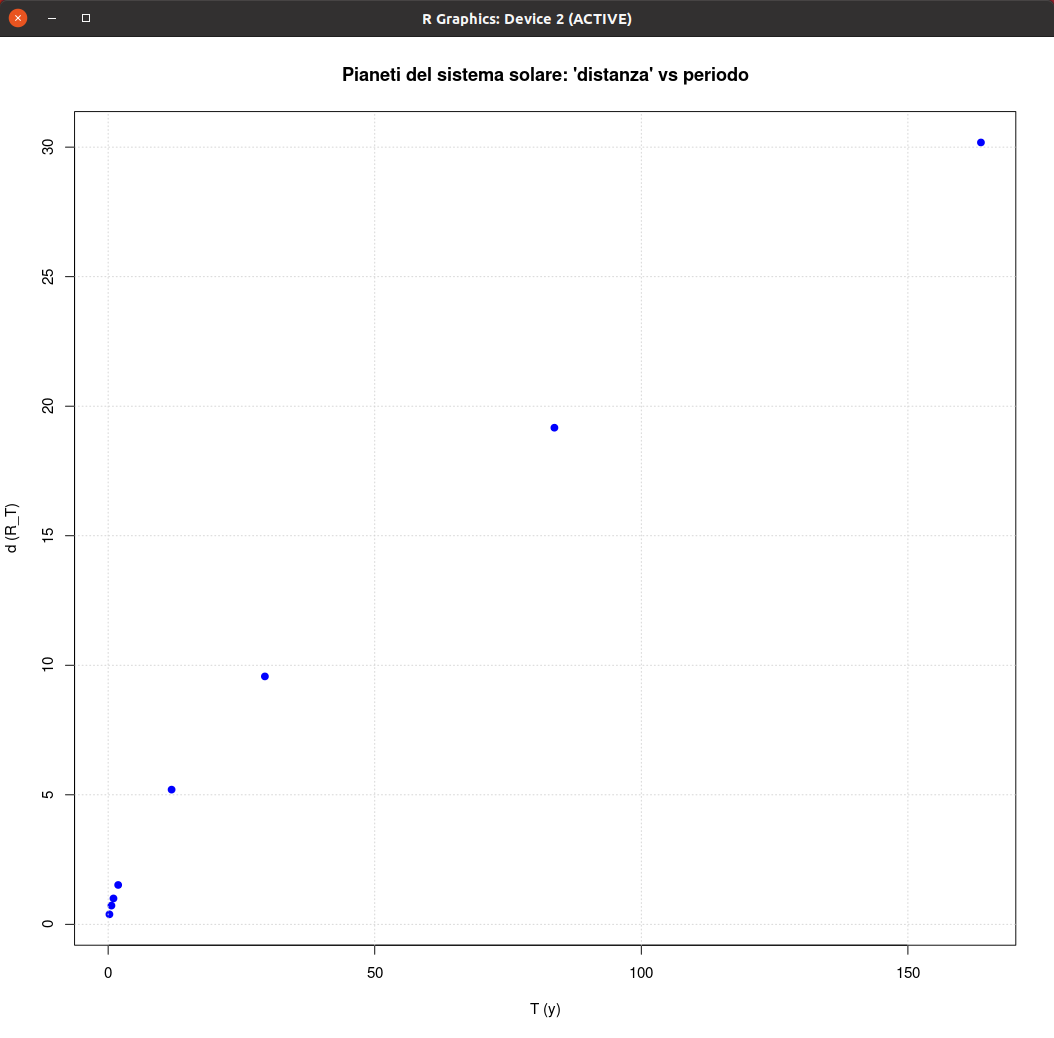
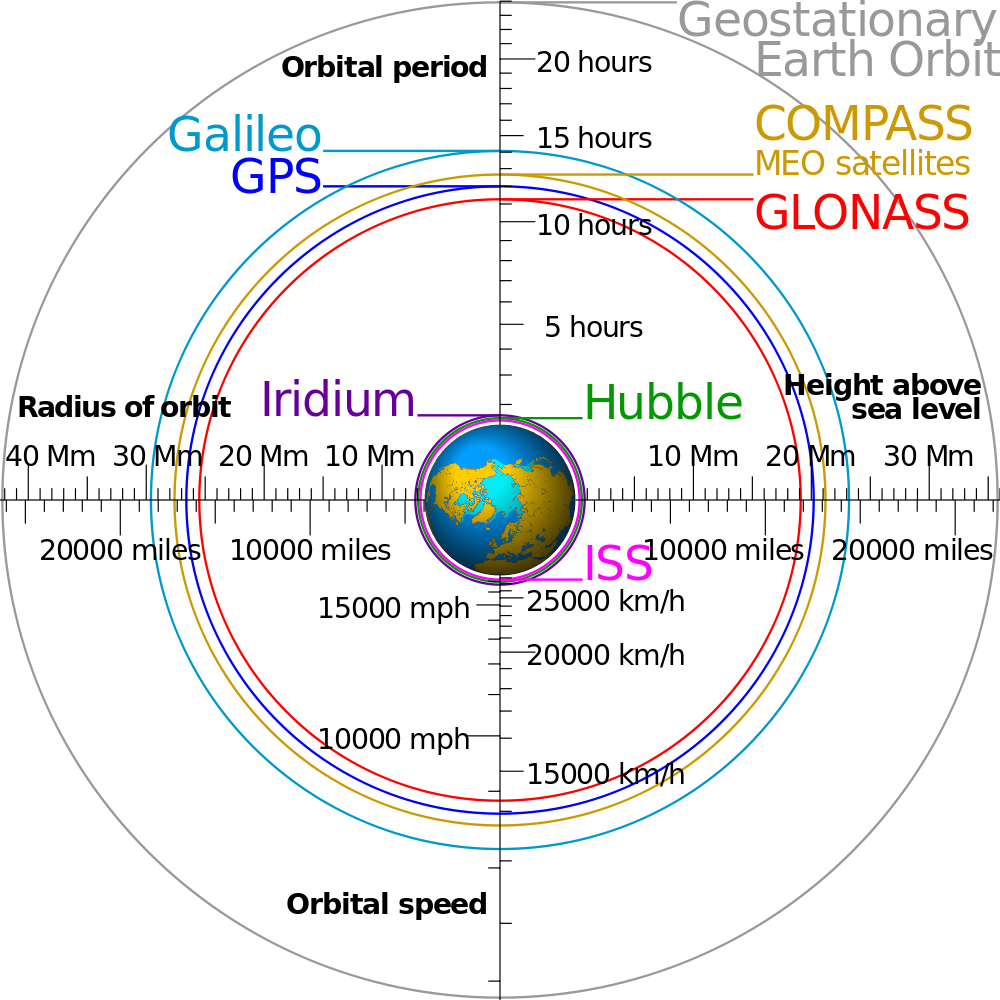
Il cosiddetto 'cannone di Newton' è un esperimento concettuale
per far capire che
le mele che cascano e la luna che gira
derivano dalle stessi leggi della Fisica.
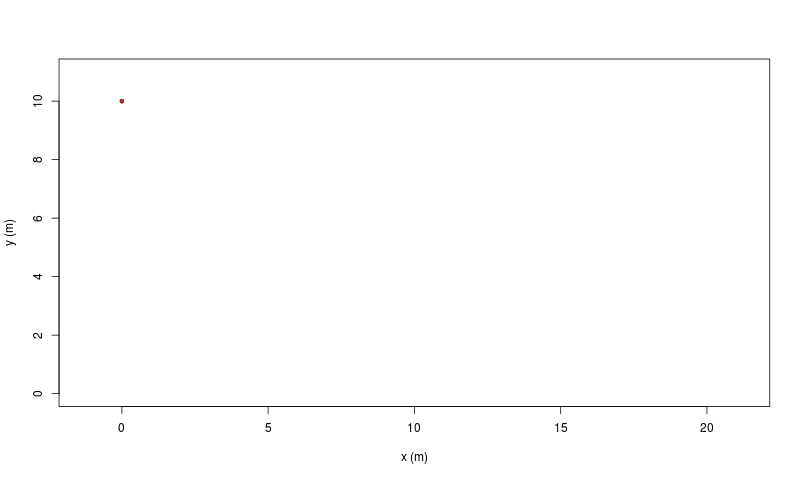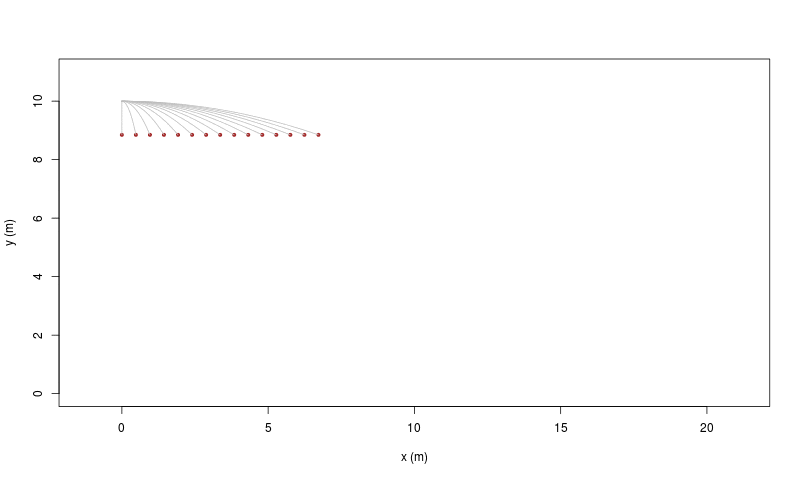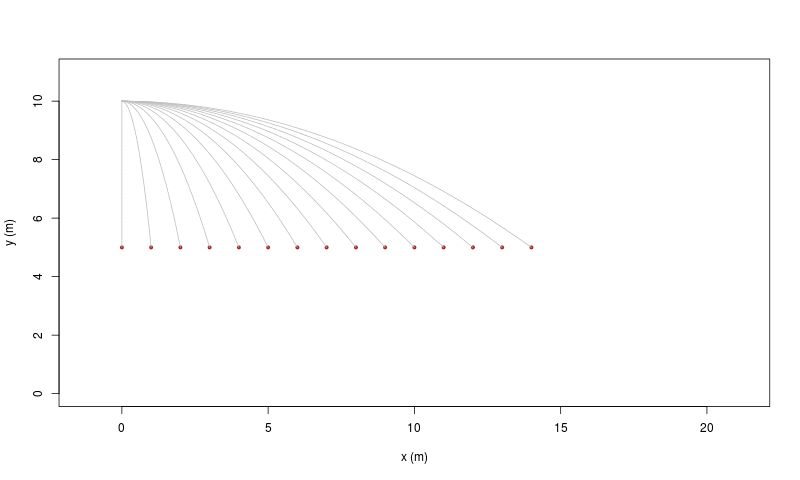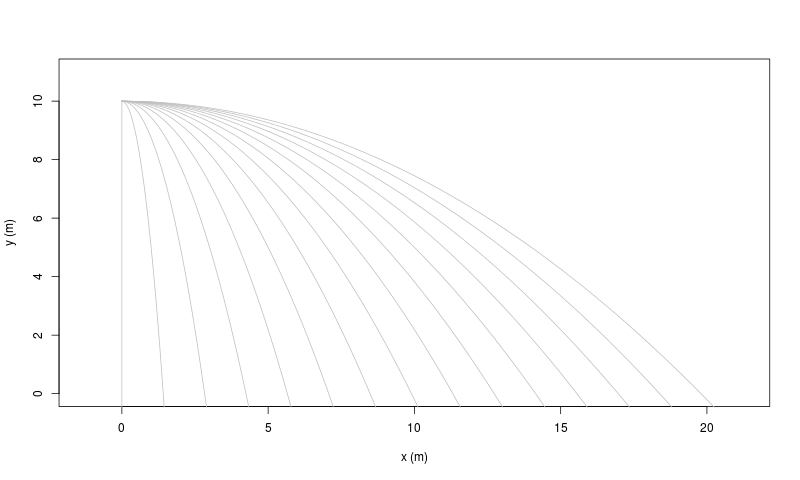
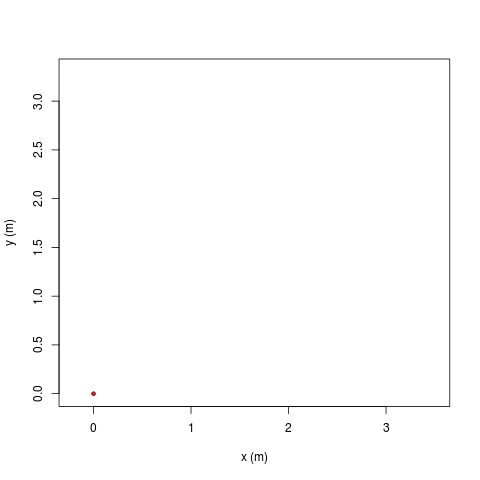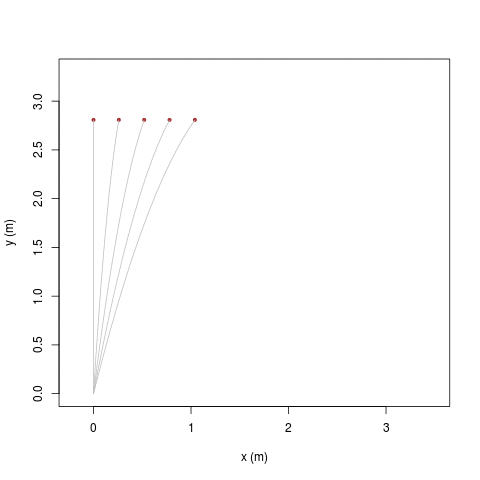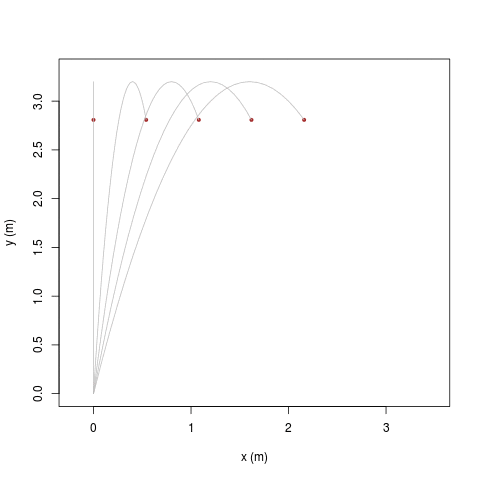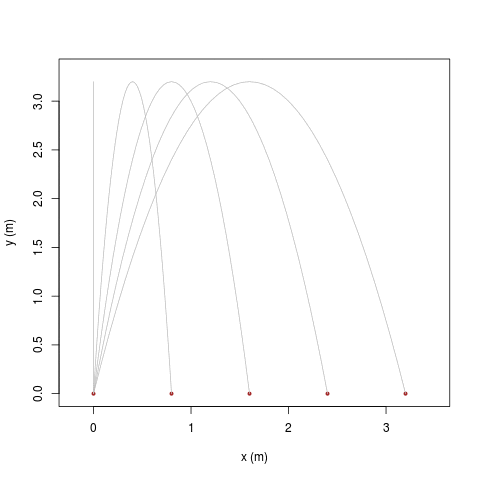 |
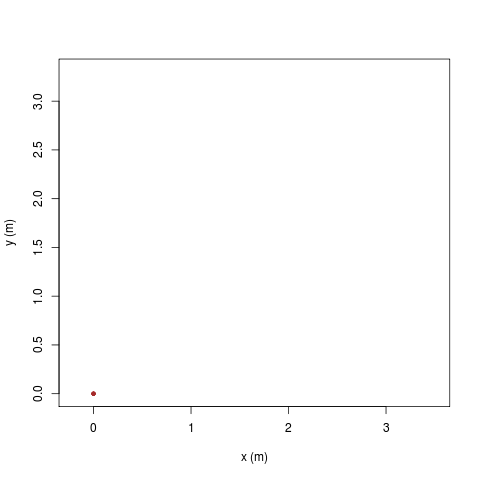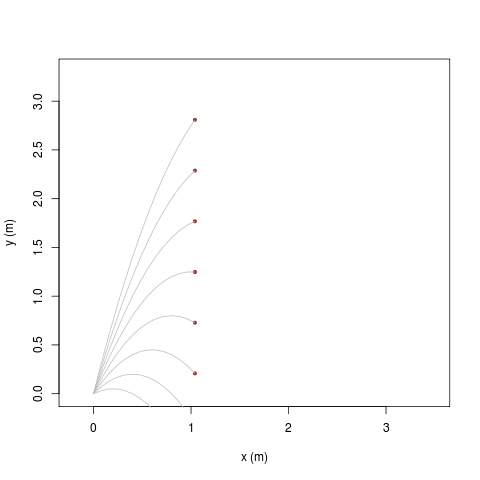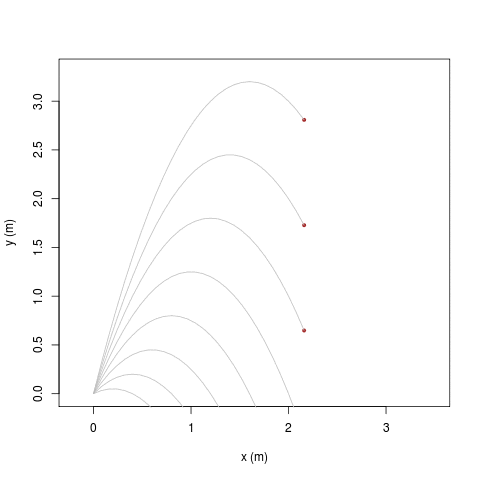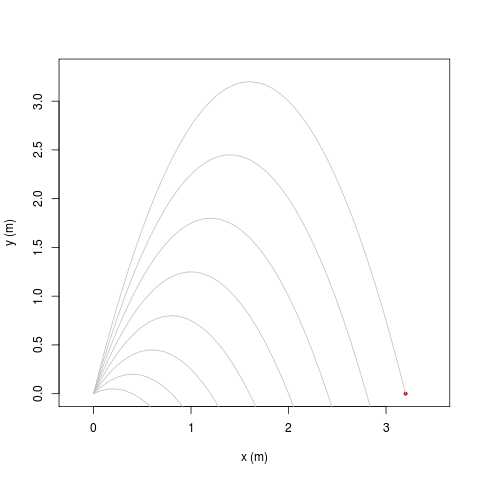 |
| [ stessa vy0; diverse vx0 ] | [ stessa vx0; diverse vy0 ] |
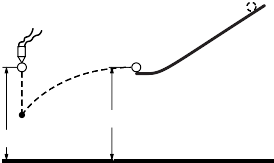
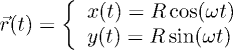
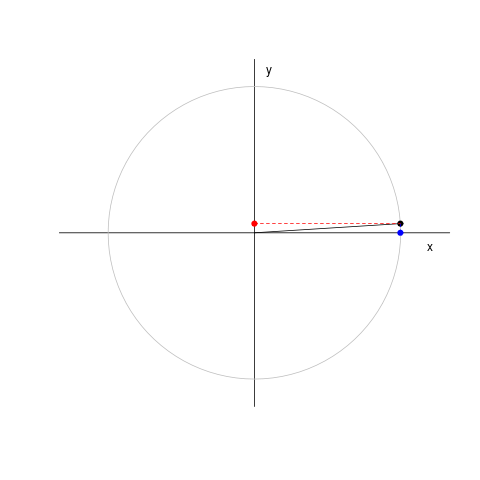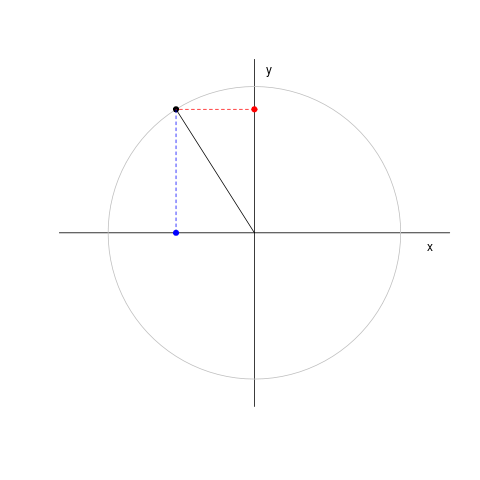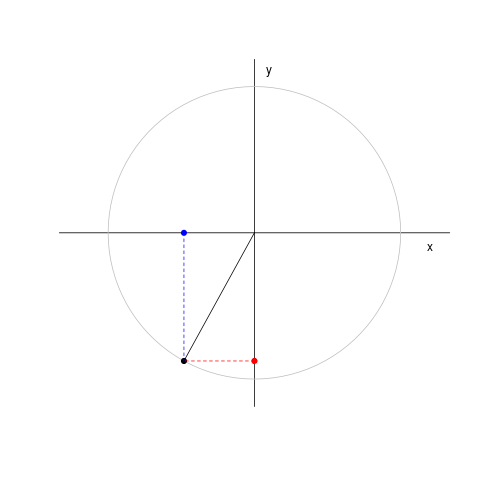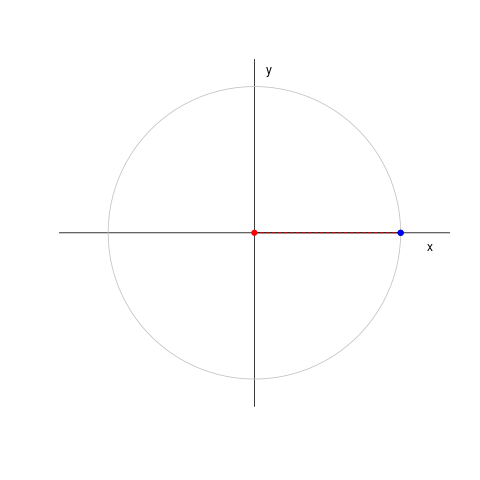
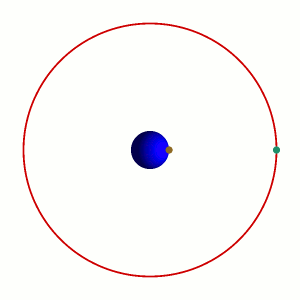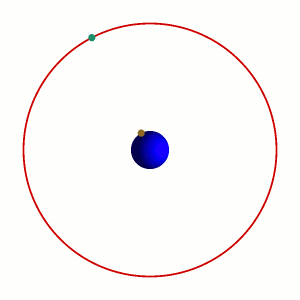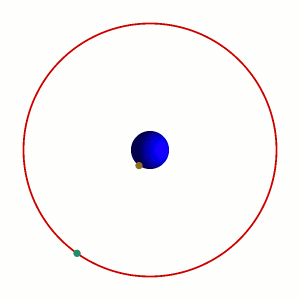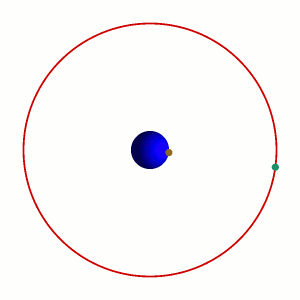




 |
 |
| Aria | Vuoto |