Galleria di immagini e link associati

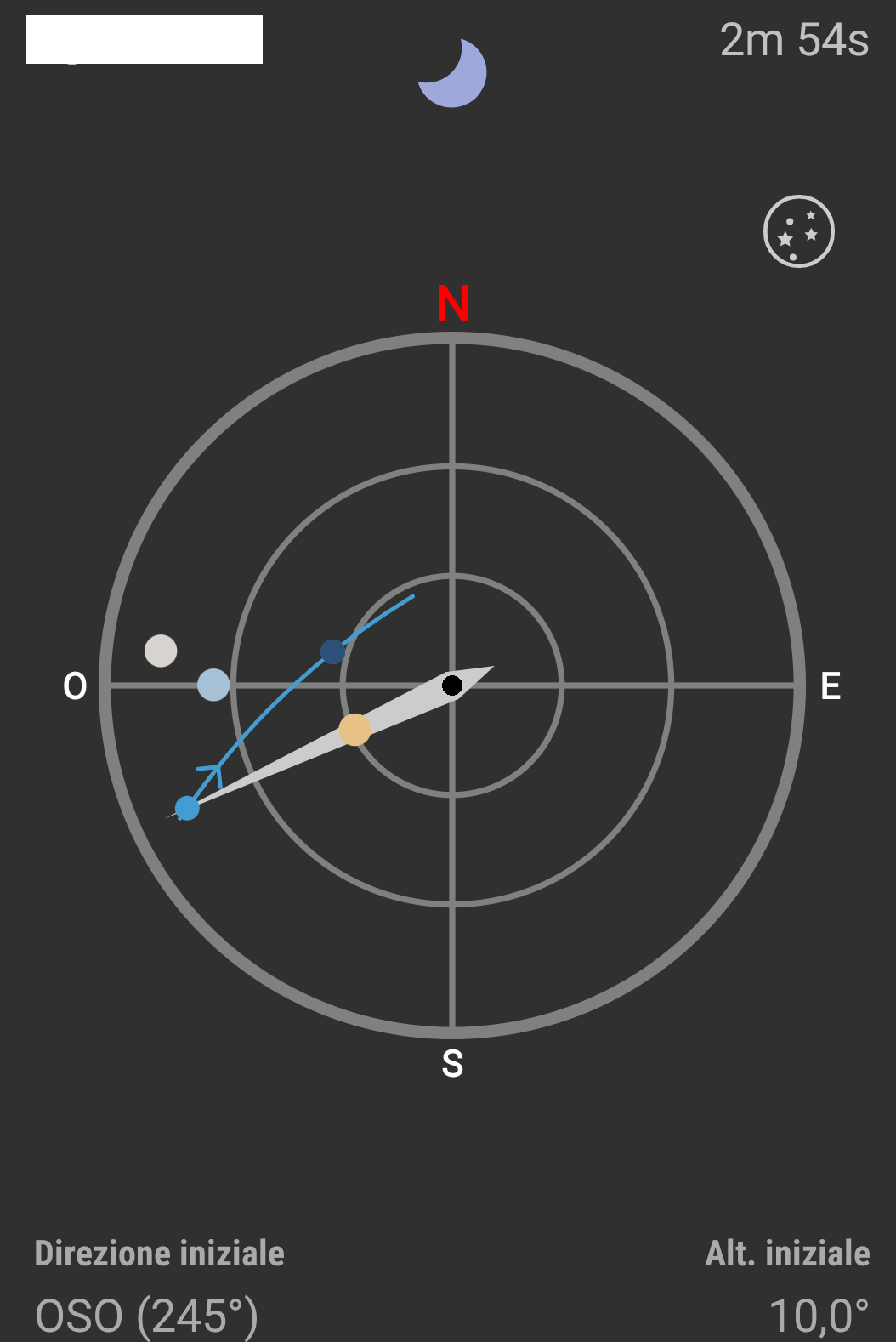
Metadata (info sulla foto)

• Sensore: 6.17mm×4.55mm, 4896px×3672px
  (vedi qui per le dimensioni tipiche dei sensori)
• Focale (vera): 123 mm
• Focale equivalente ('35mm', o 'full frame'): 720 mm
• Larghezza del cartello: 25.0 cm.

• avere grandezze adimensionali sullo stesso asse;
• poterle visualizzare al meglio sul plot.

• Le curve continue sono ottenute da f(p) = (n+1)!/(x!·(n-x)!)·p^x·(1-p)^n-x;
• le curve puntinate sono ottenute usando delle Beta (vedi script e Lezione 41);
• le linee verticali indicano i valori modali, pari a x/n;
• il valore atteso vale invece E(p) = (x+1) / (n+2) (regola di successione di Laplace)
  • esso è pari alla moda solo per x=n/2 (e vi tende per x e n-x molto grandi);
  • altrimenti è alla sua destra (per x < n/2) o alla sua sinistra (per x > n/2)

• f(x_F | n_F=5, n=10, x=3);
• f(x_F | n_F=20, n=10, x=3);
• f(x_F | n_F=50, n=10, x=3).

[Da Franco Dupré, Lezioni di Fisica, Vol. 2, vedi dispensa per la notazione]

(Esperimento di Gasparo Berti, Roma c.a 1642)

Attenzione: la formula del 'torque' (="momento della quantità di moto") τ
che appare dopo 1:10 è errata, in quanto raggio e forza sono scambiati!]

• V_R(t) indica anche l'andamento di I(t), essendo le due grandezze proporzionali.
• Siccome è in genere 'scomodo'^(*) misurare I, questa viene inferita da V_R mediante la Legge di Ohm.
  [^(*) Vedi Fig. 1.13 a p. 16 di forze_gravitazionali_e_elettriche.pdf]

[Immagine da qui, ma attenti a pubblicità invasiva — attendere/skippare]

• Venerdi 26 maggio: 22:49:55-22:53:19;
• magnitudine (massima): -4.5!
  (per confronto, quella di Venere in questi giorni è -4.3)

[Cliccare sull'immagine per vedere l'animazione]

Beccheggio in frenata

Impennata (esagerata!) in accelerazione

Dragsters

• Android
• IOS

• B → B' (B è quello del selettore di velocità, diverso da B');
• R → r;
• Quella che sembra una ν è v (velocità).

• i puntini blu rappresentano il campo magnetico uscente;
• le frecce rosse nel selettore di velocità indicano il campo elettrico;
• il verso di deflessione della figura è per ioni positivi.

Un esperimento (virtuale) riassuntivo Quali fenomeni si vedono o si evincono? (Dal punto di vista circuitale, energetico e luminoso)
→ provare descrivere la rete di connessioni causali fra i vari processi fisici chiaramente visibili o che si evincono
→ (ad esempio: cosa determina la temperatura a regime del vetro della lampadina?)

---

Batteria per autoveicolo Notare le specifiche riportate:

• 12 V;
• 730 A;
• 75 Ah.

[Per 'V', 'Ah' e 'Wh' (e anche 'W' e 'km/h' massimi) per le bici elettriche vedi ad esempio

[Curve di energia potenziale a seconda dei segni delle cariche]

• La scala delle ascisse è in unità dei raggi terrestri.
• La scala delle ordinate è in unità del modulo del potenziale sulla superficie (con zero all'infinito).
• Script R: potenziale_Terra.R

• Pensarci bene per fare mente locale (almeno qualitativamente)
• In particolare, quanto vale per r=0?
• Vedere quindi, ma solo dopo averci pensato prima, qui

• curve_test_ingresso.R
• curve_test_ingresso_l.R
• curve_test_ingresso_ll.R

• termalizzazione.R
• termalizzazione_log.R (attenzione a cosa compare sull'asse delle ordinate!)

• Fotocamera: vecchia Nikkormat a rullino ("35 mm", ovvero fotogrammi da 24mm×36mm);
• obiettivo: f=50 mm;
• la pellicola è stata sostituita con un foglio di carta lucida 'da disegno' di una volta (va bene anche la carta da forno);
• il 'filo' in alto a destra è il flessibile, che serve a mantere l'otturatore aperto indefinitivamente.

[dimensioni in mm]  
 

 

• attraversano l'acqua fino alla finestrella disegnata sulla bottiglia;
• escono in aria obbedendo alla 'ben nota' legge di Snell.

 

Raggi notevoli per la costruzione delle immagini in 'lenti sottili'  
Nota: Anche nel caso delle lenti, oltre al raggio parallelo e quello (o suo prolungamento) passante per il fuoco, c'è un terzo raggio 'notevole', in questo caso quello passante per il centro (in rosso nella figura e chiamato dagli autori della stessa 'raggio M').
Ma è bene abituarsi ad usare preferibilmente i primi due, che sono di validità più generale e per l'analogia fra specchi e lenti.

---

---

• Si noti la linea verticale tangente allo specchio nel punto in cui esso interseca l'asse ottico:
  → equivalente a quella usata a lezione per ricordare che siamo in approssimazione parassiale ('di Gauss').
• Altre chiarimenti e suggerimenti di uso nei Dettagli delle lezioni.

Uso stradale di specchi convessi Per una curiosa applicazione degli specchi convessi, in voga secoli fa per osservare (specchiati) i paesaggi,
si cerchi

     

Specchio concavo

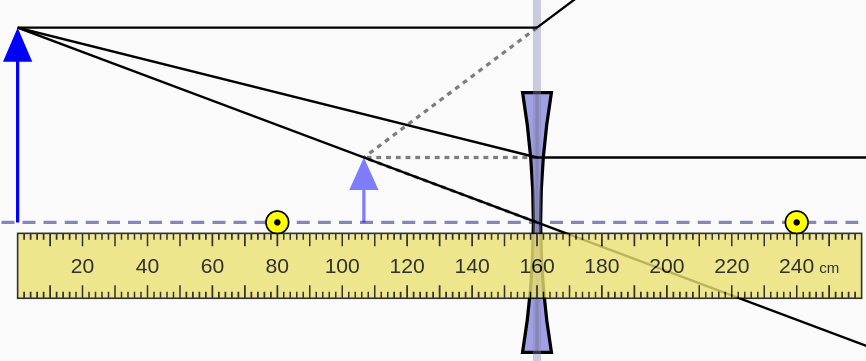
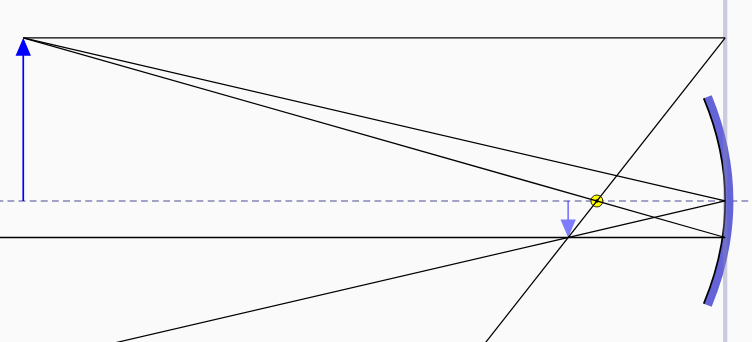
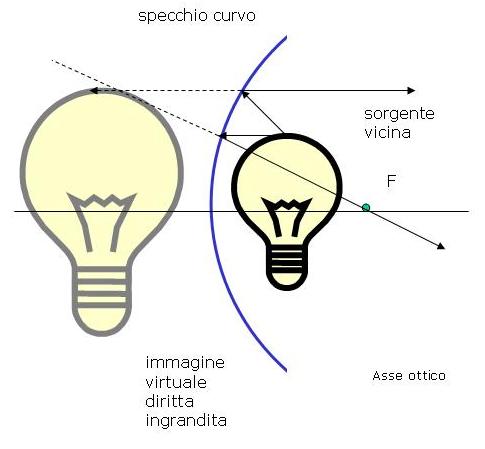
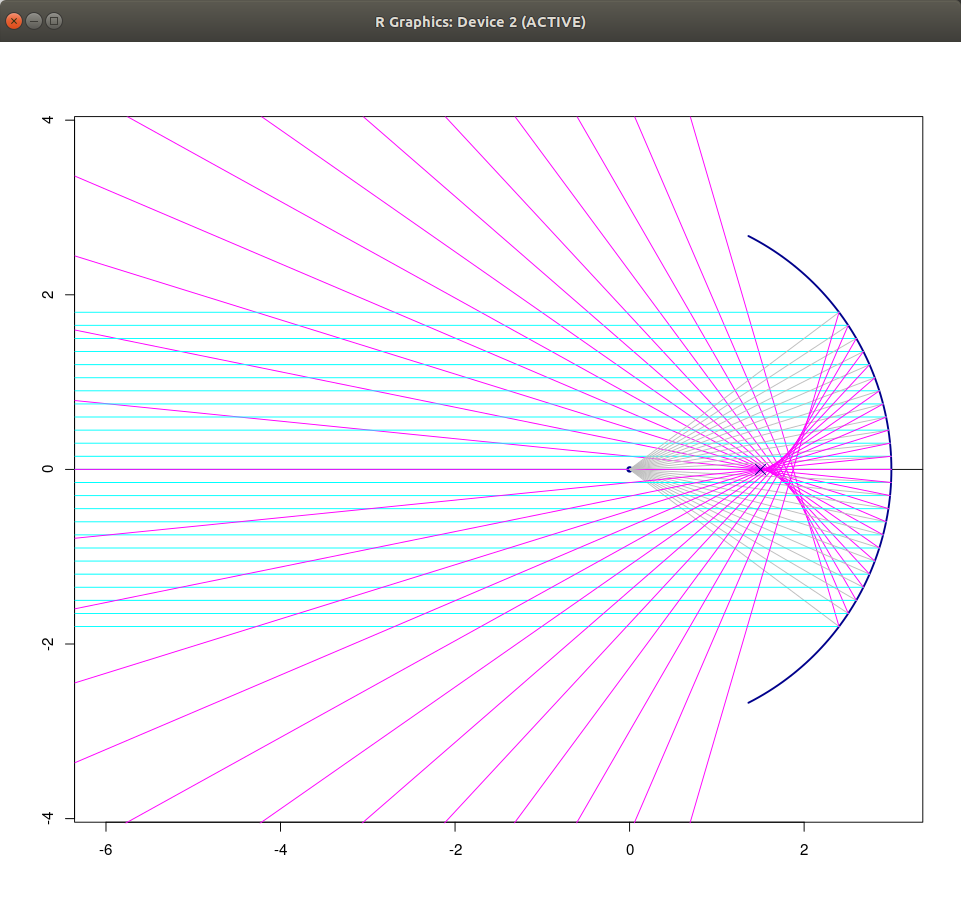
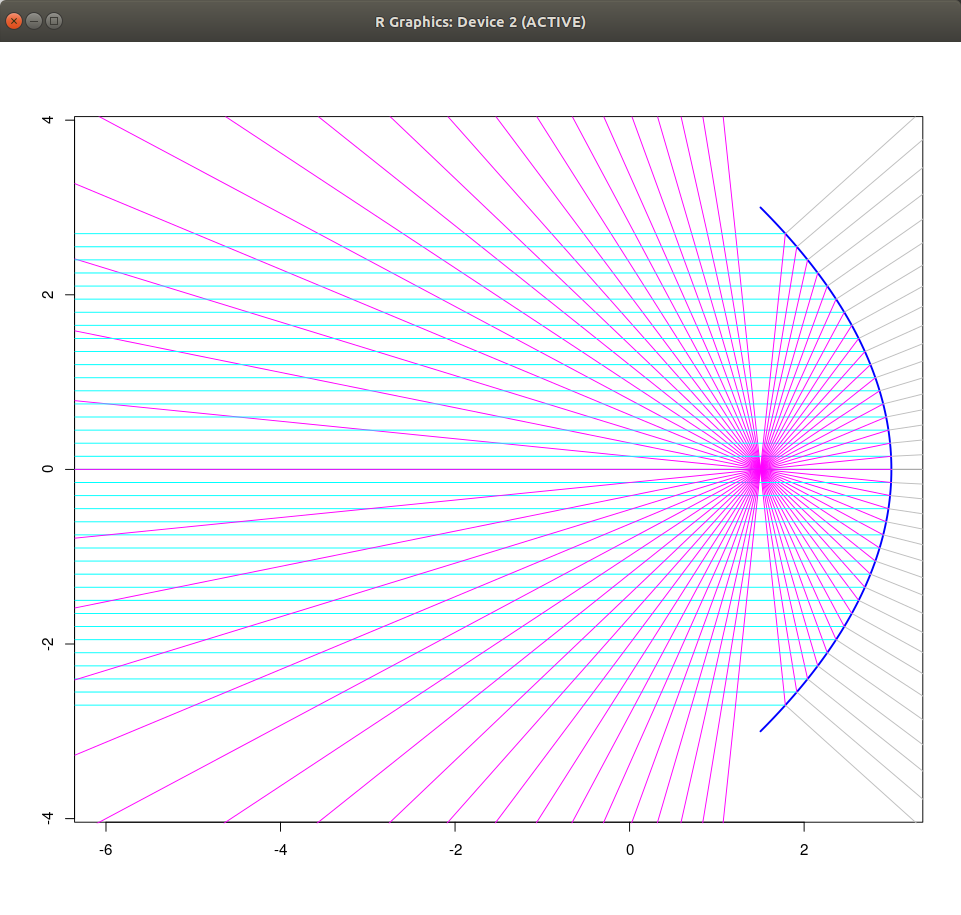
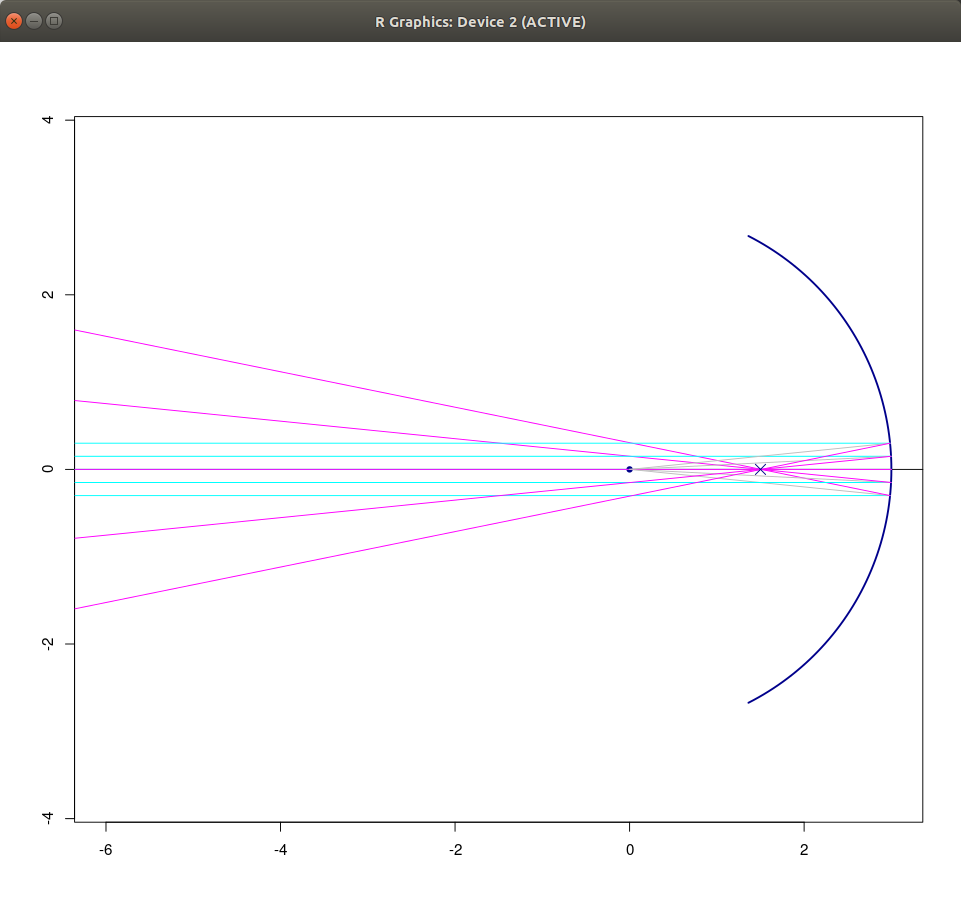
oggetto oltre il fuoco	oggetto fra specchio e fuoco

---

Schema qualitativo di immagini reali e virtuali Si raccomanda di prendere esperienze con immagini reali (ad es. di lampadine) facendo uso di 'specchi concavo' casalinghi, come cucchiai, mestoli e tazze.
→ si dovrebbe vedere l'oggetto riflesso fluttuante nell'aria, fuori dallo specchio.

---

• Nota: la forma non è sferica, bensì parabolica → antenne paraboliche.
• Nota storica: Specchio ustorio

   

       

Specchio piano: schema di formazione dell'immagine

---

---

     
 

 

 

[La figura (b) mostra dettagli tecnici che vanno al di là di quanto possiamo fare in questo corso]

• Scegliere Fenditure;
• scegliere il generatore luminoso (a destra del simbolo dell'altoparlante);
• scegliere il numero di fenditure;
• 'giocare' con gli altri parametri.

[0° → orizzonte; 90° → zenith]

• Simulazione di luce in una goccia d'acqua (solo arcobaleno primario)
• How do rainbows form?

 
[Arcobaleno alle 9:27 del 7 dicembre 2020 - Particolare sul palazzo in costruzione]

 
[27/3/2015 18:09]

• sequenze dei colori dell'arcobaleno primario e secondario;
• diversa tonalità nelle regioni di cielo delimitate dagli arcobaleni (quella fra i due arcobaleni è chiamata banda di Alessandro).

Dipendenza dell'indice di rifrazione dell'acqua dalla lunghezza dl'onda
  Immagine presa

Riflessione

 
Rifrazione

• Mirage
• Fata Morgana

 

• fourier_oq_a.R
  fourier_oq_b.R
• fourier_otr_a.R
  fourier_otr_b.R

• in basso sorgente (laser);
• a sinistra e in 'alto' (in figura — il tutto è su un piano): specchi riflettenti;
• a destra: ricevitore;
• 'dopo' la sorgente (e 'prima' del ricevitore): specchio semitrasparente.

• se il sistema è stabile: interferenza distruttiva sul ricevitore → segnale nullo;
• se i 'bracci' (di c.a 4 km!) si allungano o si accorciano: → segnale non nullo;
• rivelatore sensibile a variazioni di lunghezza di una piccolissima frazione di lunghezza d'onda!

 
26/04/2023, ISO 125, f/5.6, 1/500 s, f=300 mm ['450 mm equiv. 35mm film']

Si fa presto a dire termometro...
(sempre a proposito di principio di misura)  
(+

• Provare a cambiare la temperatura (riaggiustando eventualmente le scale);
• provare ad attivare le varie opzioni;
• prestare attenzione a come cambiano (qualitativamente), in funzione della temperatura,
  • l'intensità emessa nel visibile nel visibile;
  • l'intensità emessa nell'infrarosso;
  • l'intensità emessa nell'ultravioletto.
• Si noti la differenza (in particolare l'unità di misura!) fra Spectral Power Density, riportata nell'asse delle ordinate e Intensity, stampata se si spunta l'omonima opzione.

Figura da prendere cum grano salis perché potrebbe confondere più di quanto chiarisca (scaricata da link che ora dà problemi)

• Per una tabella di riferimento dei lux richiesti in diversi ambienti vedi ad esempio qui o qui (NORMA UNI-EN 12464),
  dalle quali si evince, dalle misure effettuate con i luxmetri delle app, come l'Aula Pasquini sia scarsamente illuminata (non solo quando ci hanno girato il film!).
• L'illuminamento dovuto alla Luna piena è dell'ordine di grandezza del lux, in realtà inferiore a mezzo lux (vedi sul link italiano anche ulteriori chiarimenti sulla differenza fra lux e lumen).
• Luce richiesta (in termini di intensità e 'qualità') nelle serre (e dalle piante in generale),

 

Compressione e decompressione di una molla

Compressione e decompressione di aria

Oscillazione trasversale di una molla

Oscillazioni verticali locali del livello dell'acqua

• Illuminance - Recommended Light Level
• Illuminazione ambienti ospedalieri
• Illuminazione posti di lavoro
• Come illuminare casa

• I puntini rossi aiutano a visualizzare l'oscillazione sinusoidale nel tempo della grandezza fisica^(*) per una posizione prefissata lungo la linea di propagazione dell'onda.
   
• Ogni singolo 'fotogramma' dell'animazione mostra invece l'oscillazione sinusoidale nello spazio della grandezza fisica^(*) per un tempo prefissato (è chiaro il concetto di lunghezza d'onda, misura della periodicità spaziale).
  Ecco alcuni esempi, ottenuti estraendo i fotogrammi dalla gif animata:
                 
  (La gif animata è costituita da 150 fotogrammi)

(Notare le oscillazioni dei puntini rossi!)

• lo zoom di quella a sinistra intorno al minimo,
• ridefinendo lo zero dell'energia potenziale al valore di minimo.

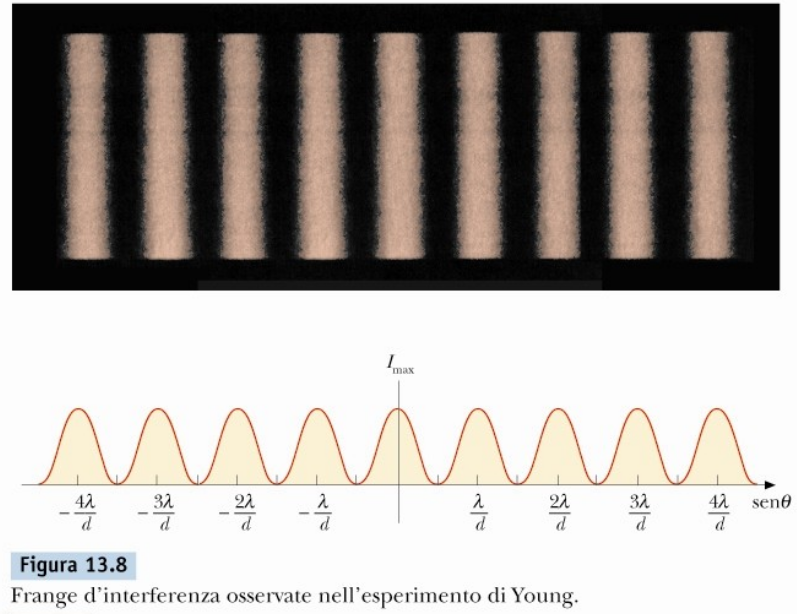
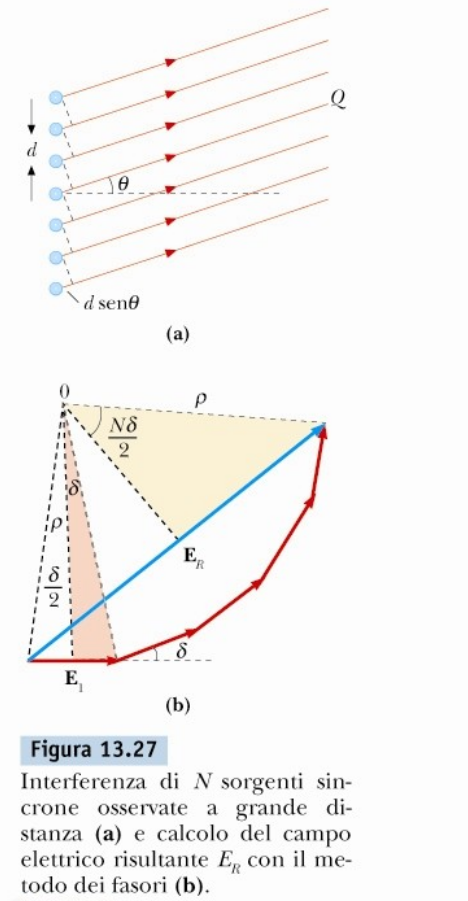
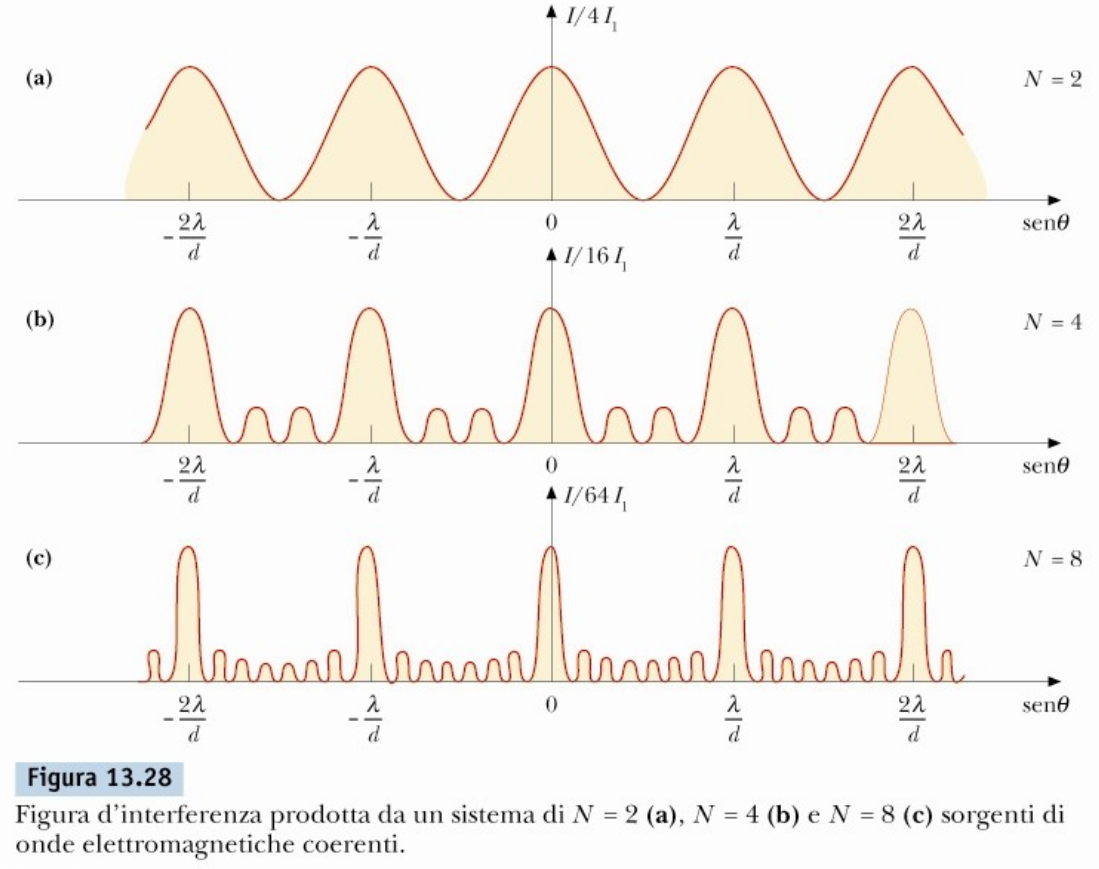
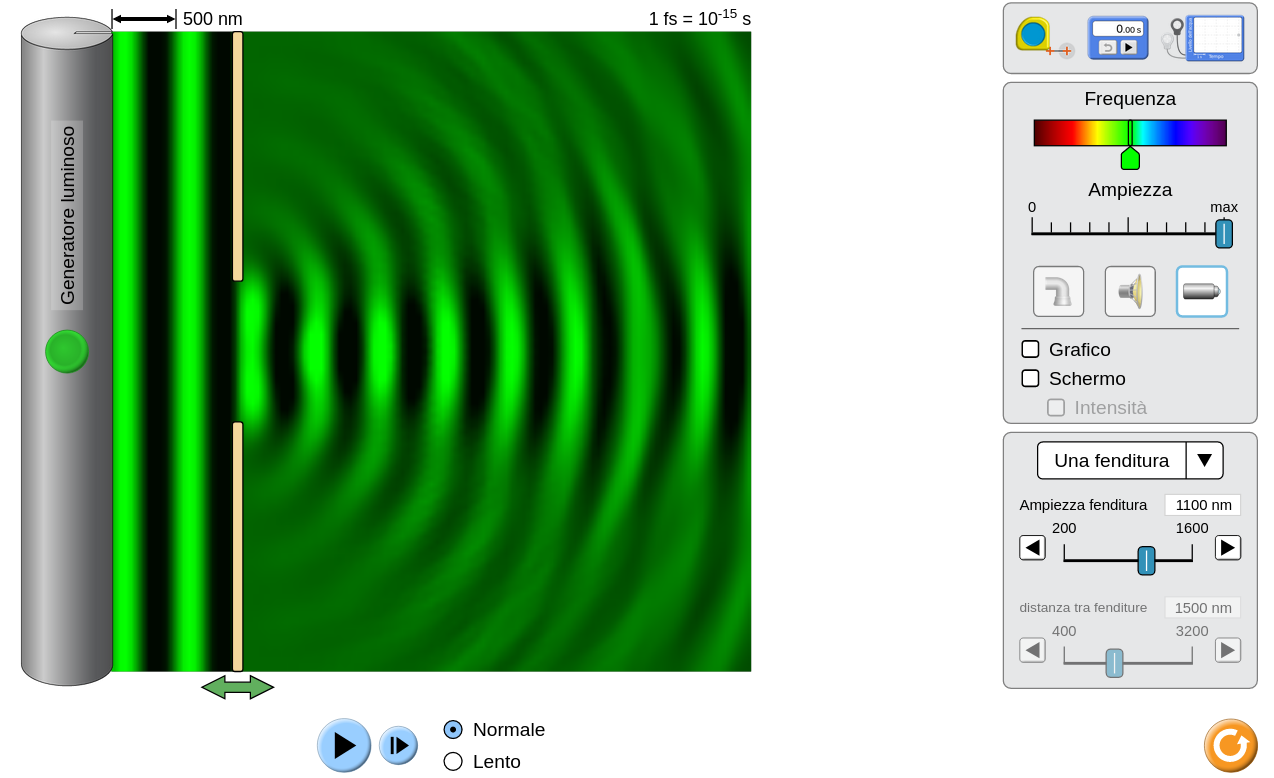
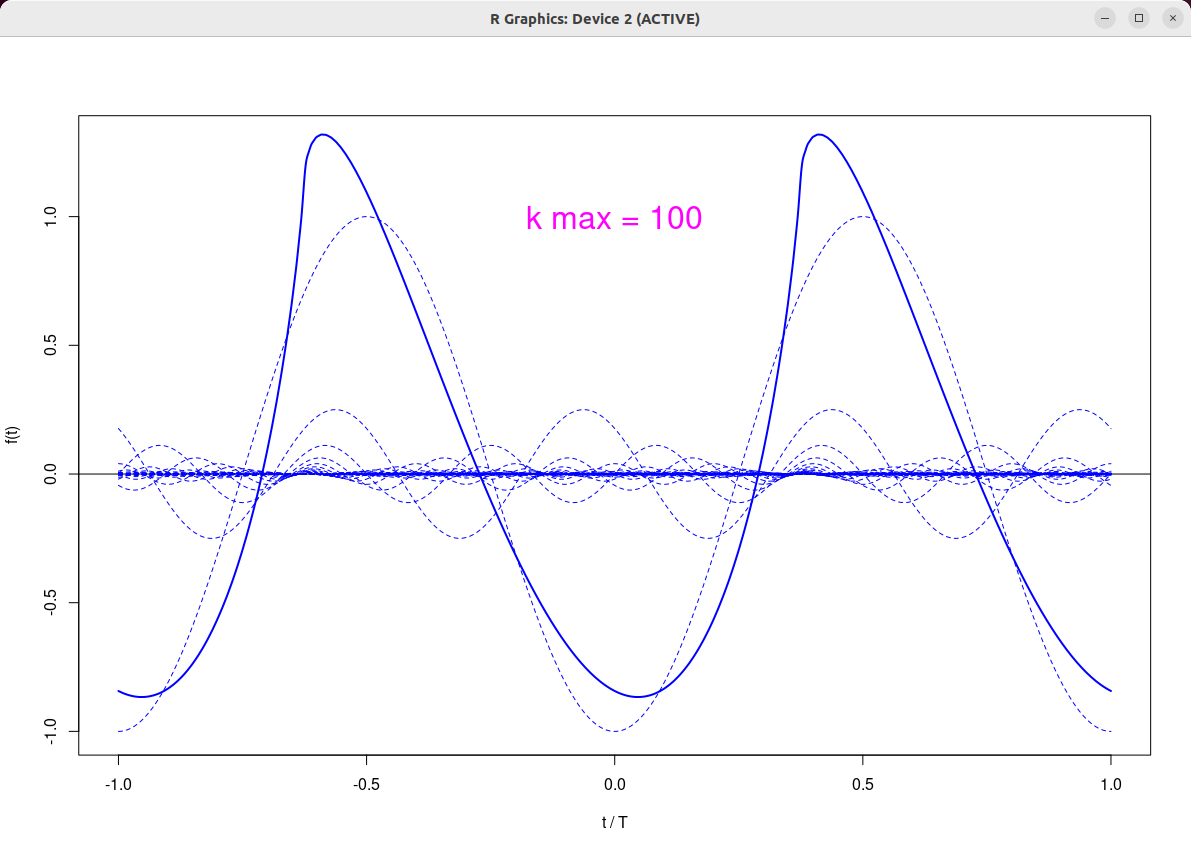
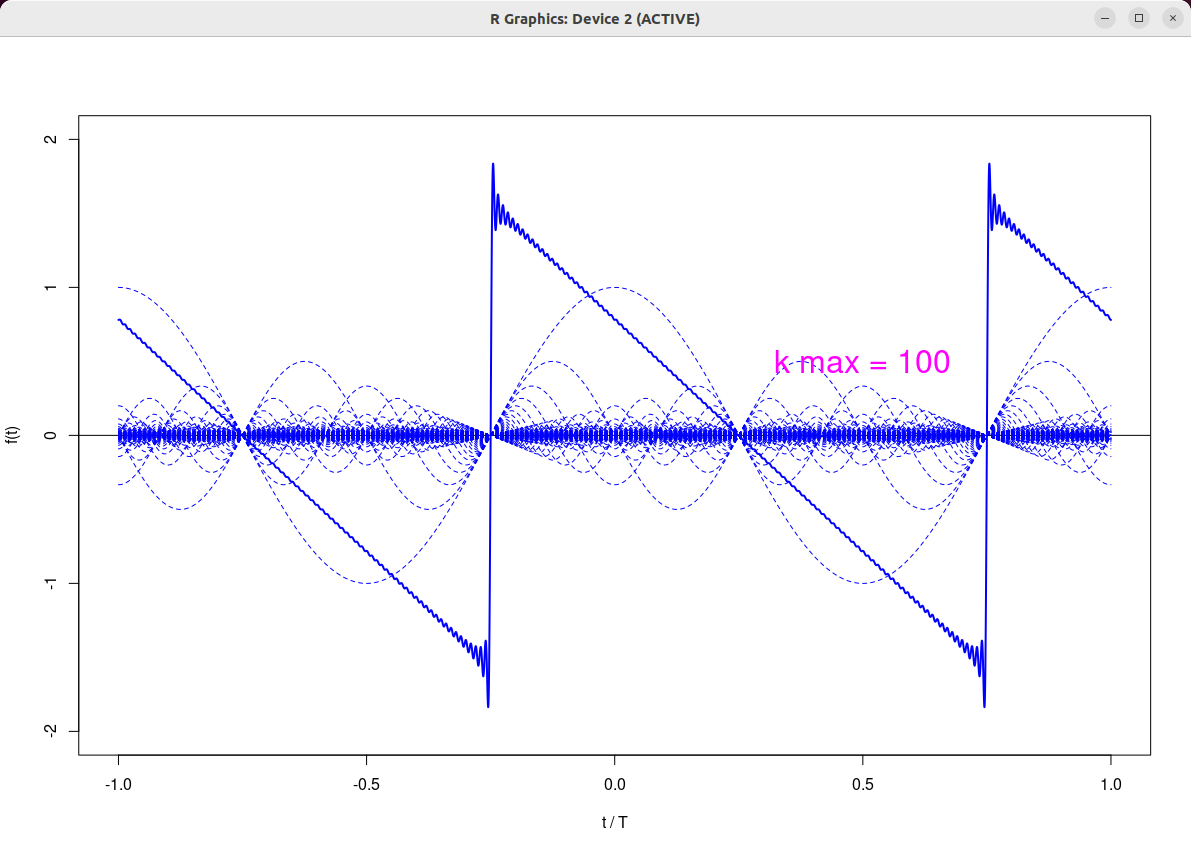
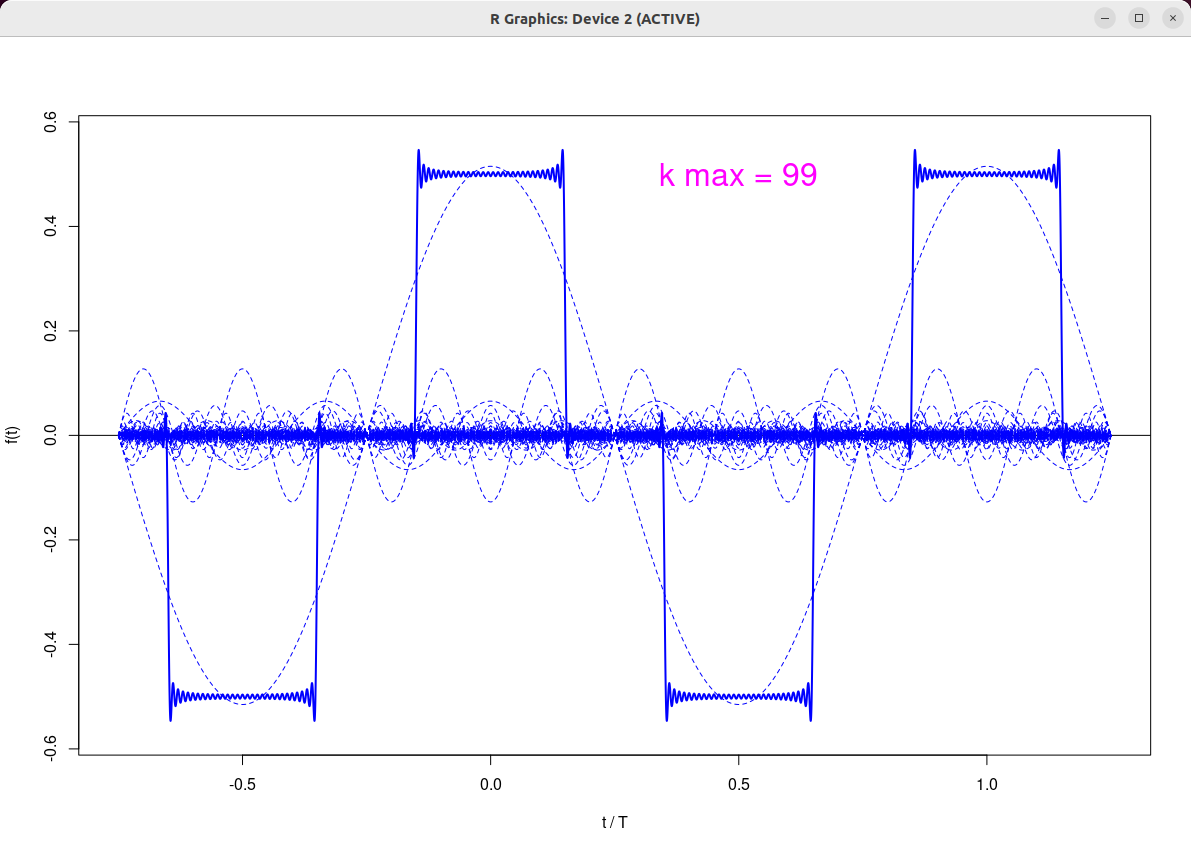
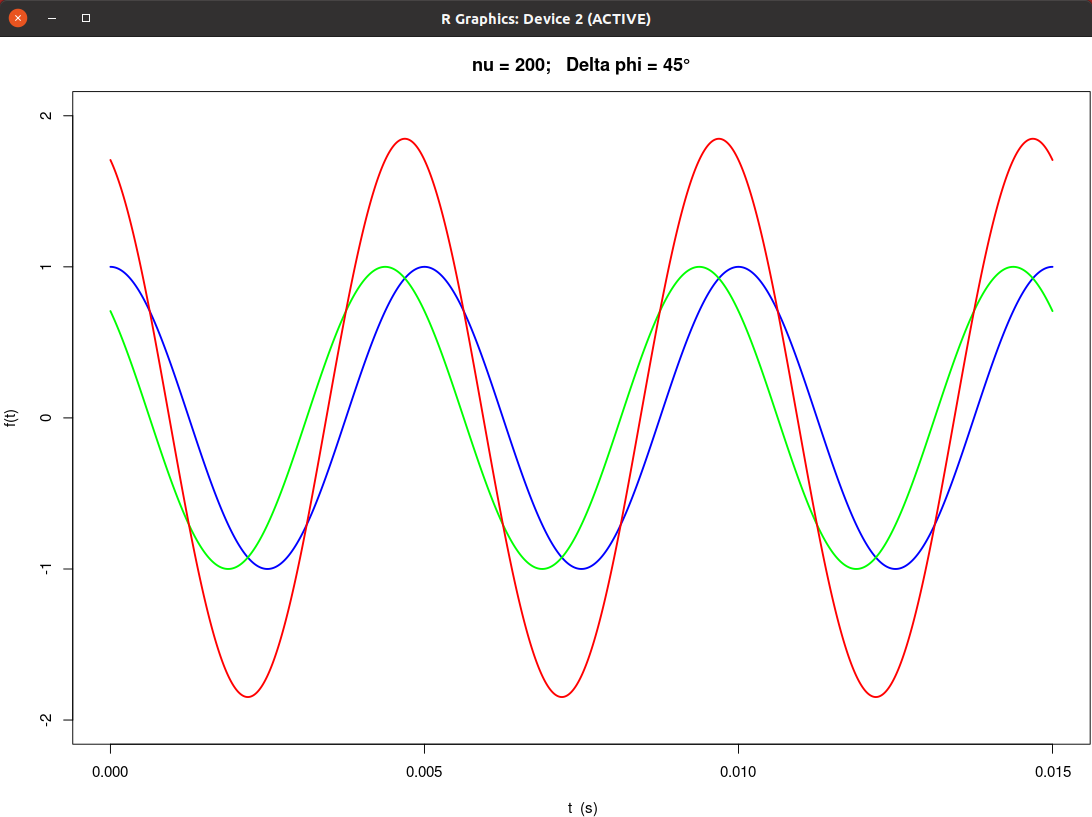
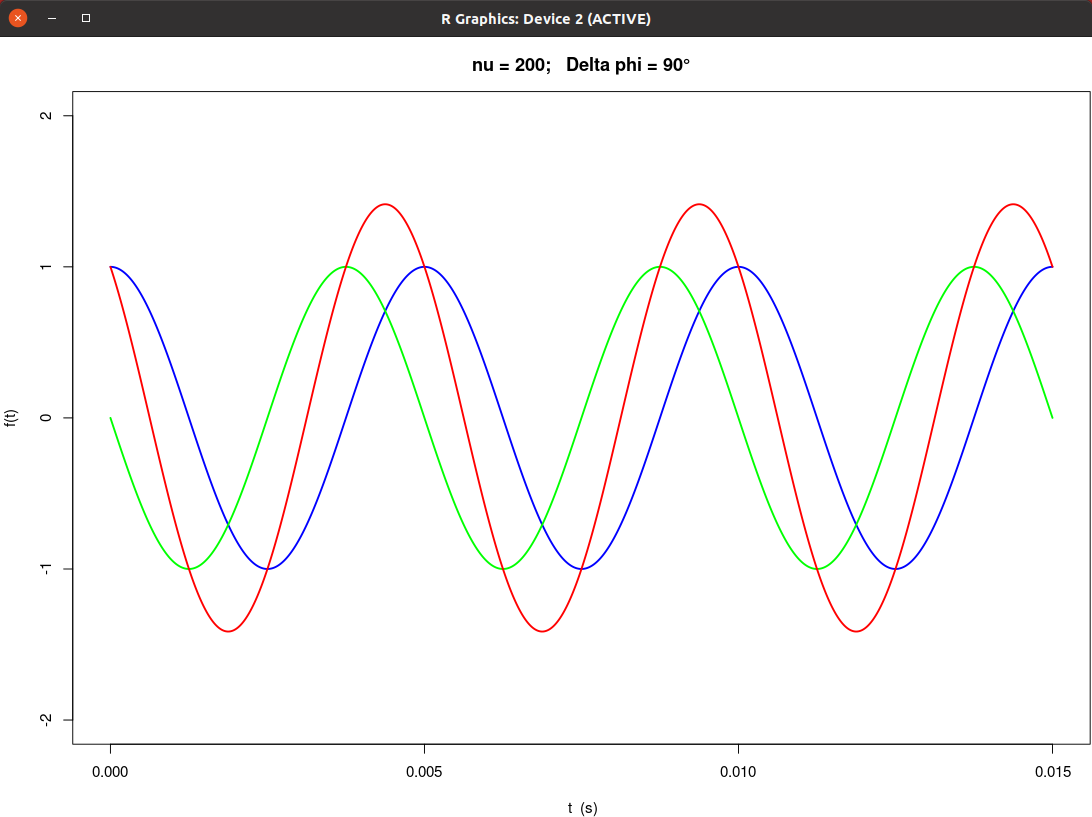
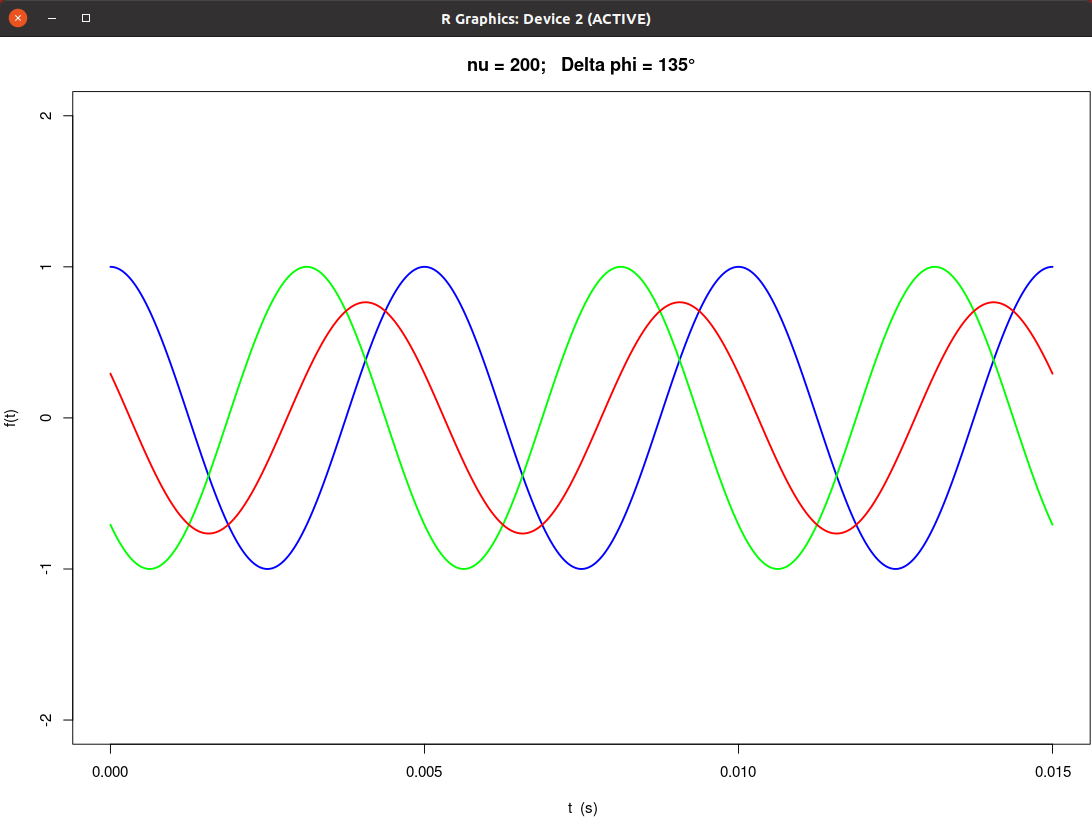
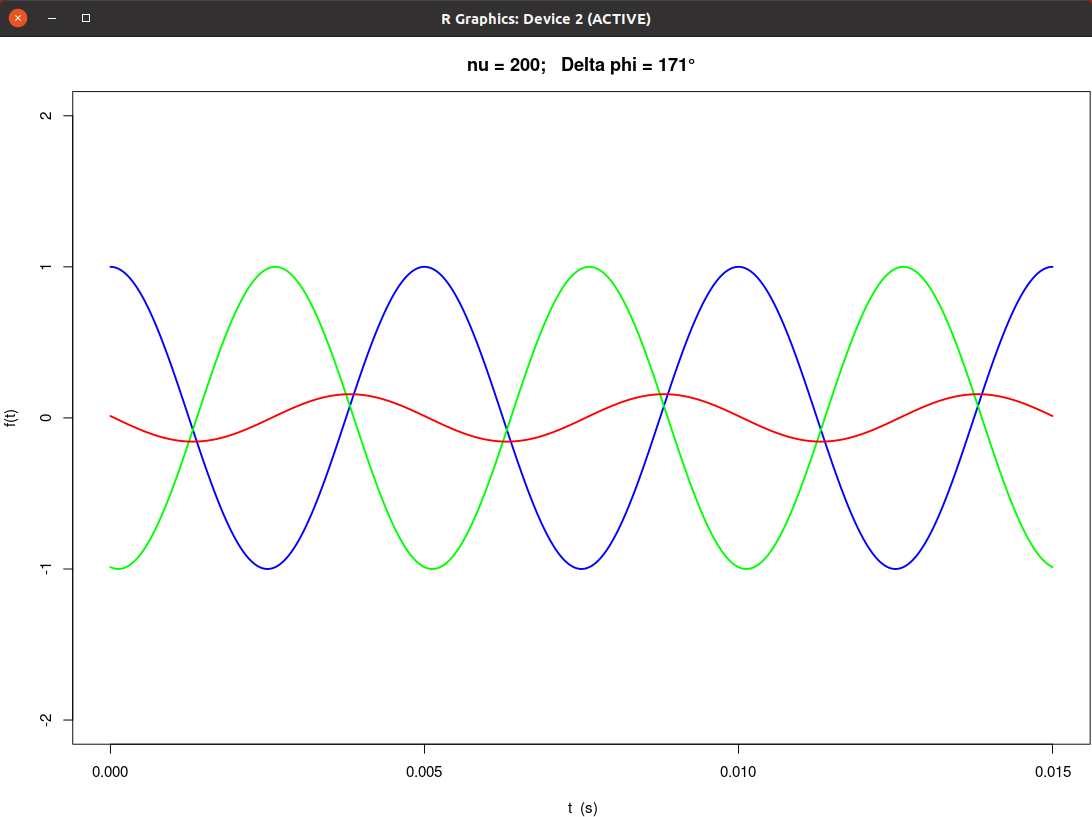
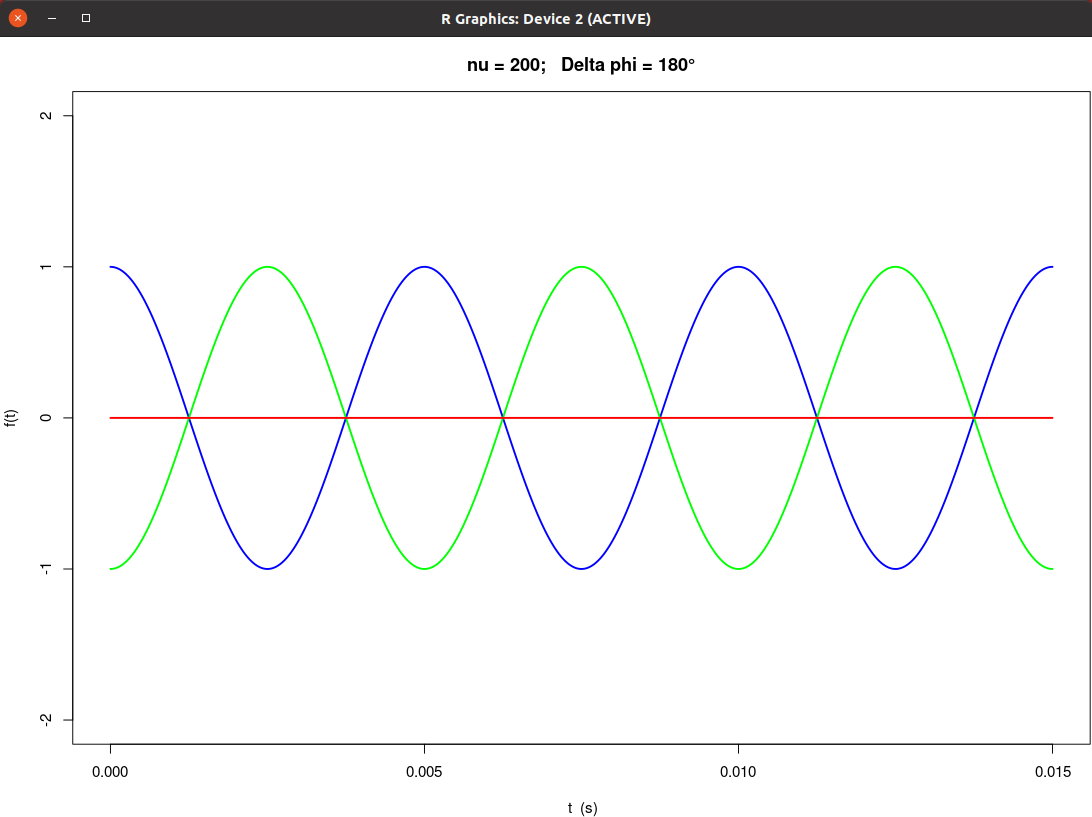
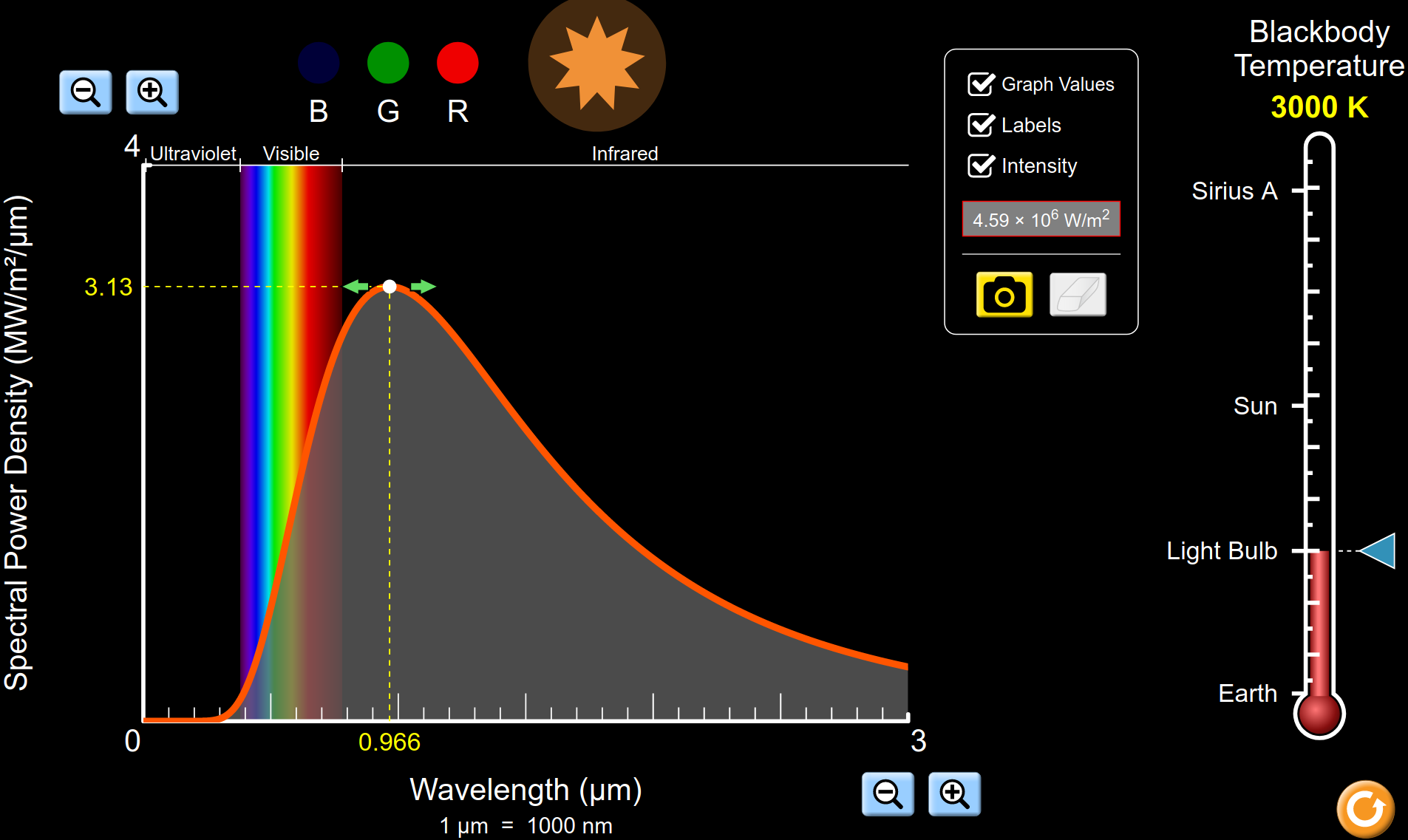
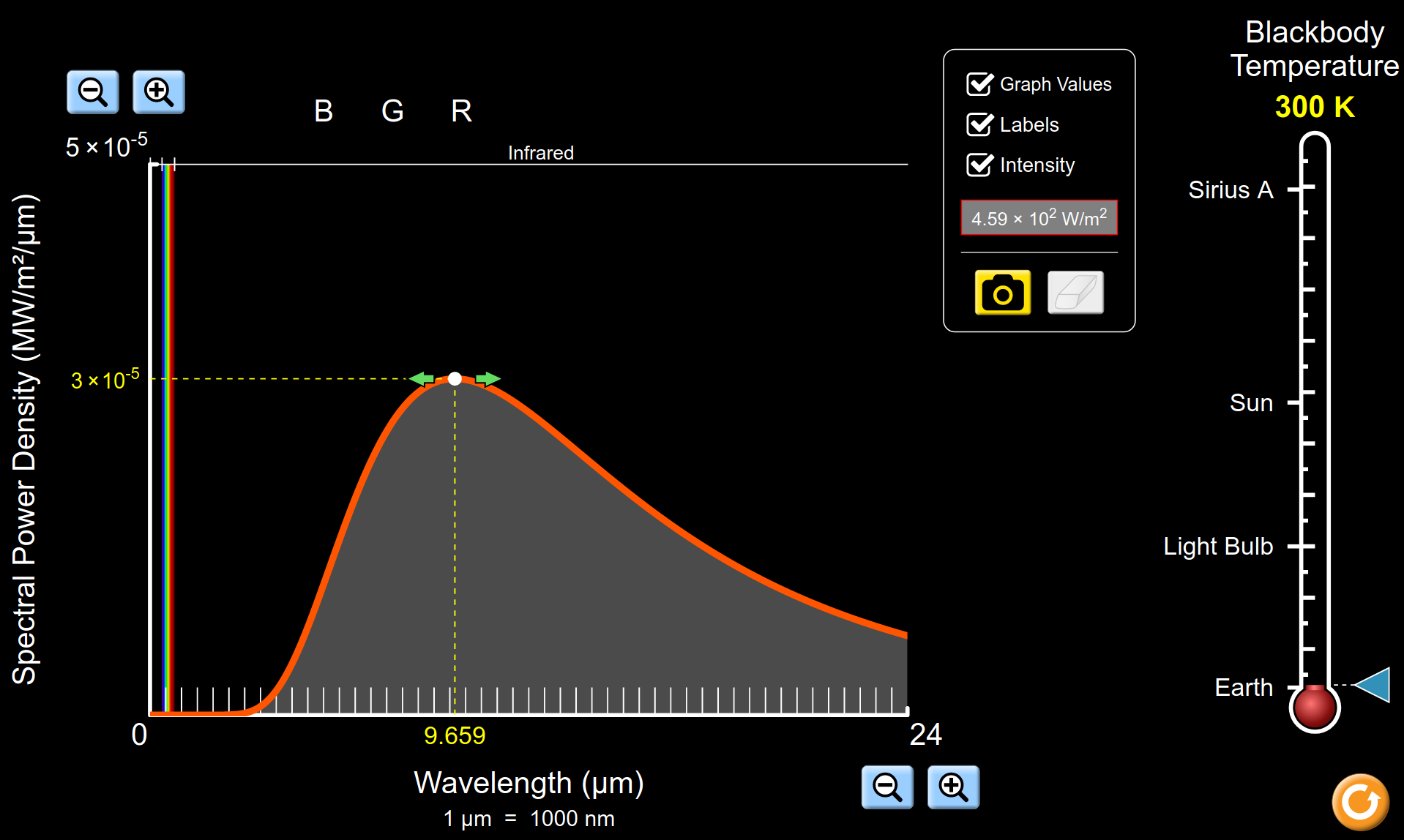
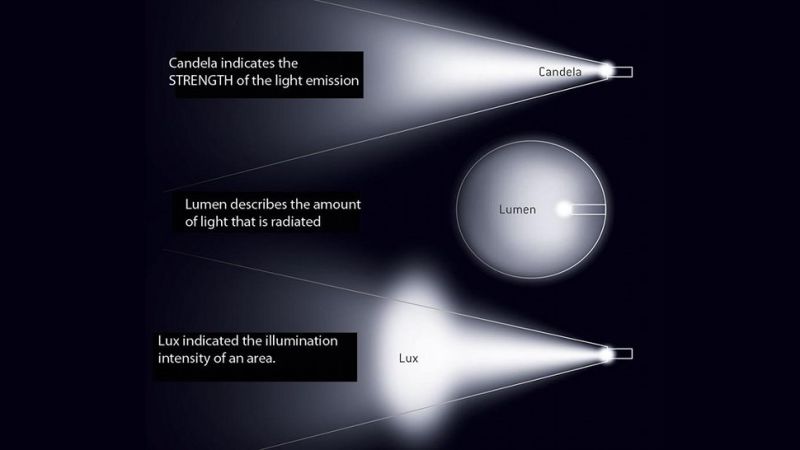
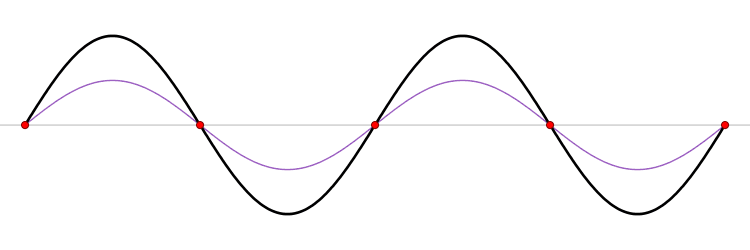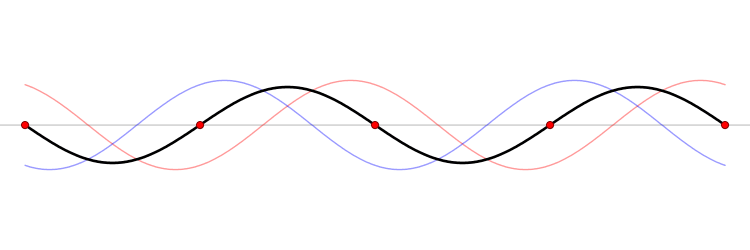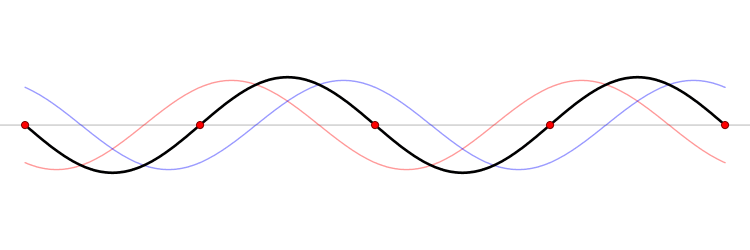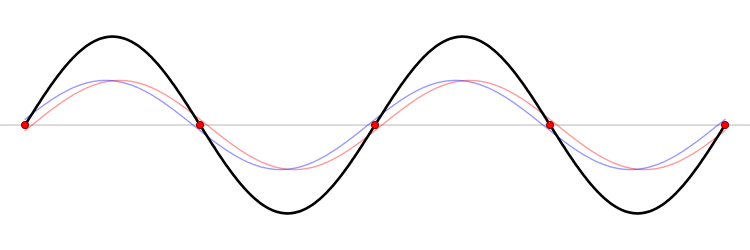
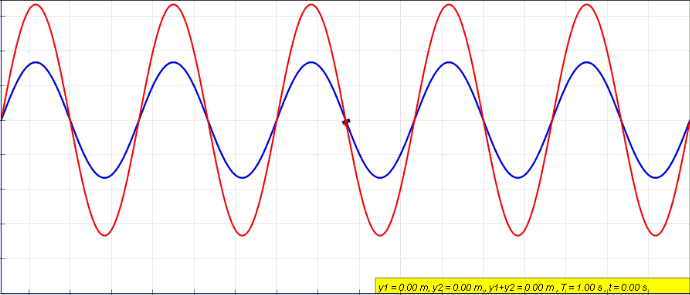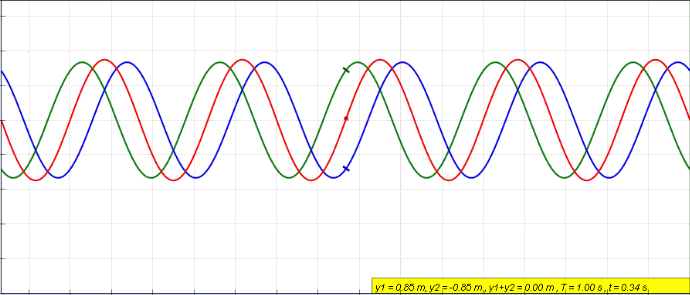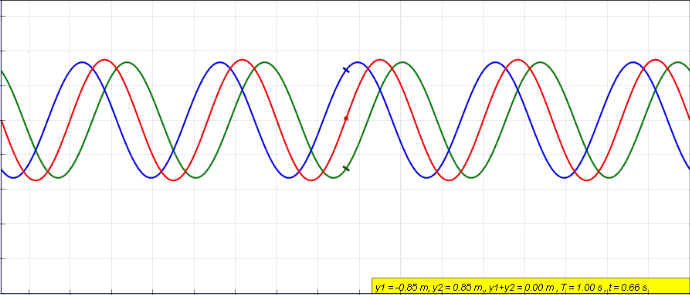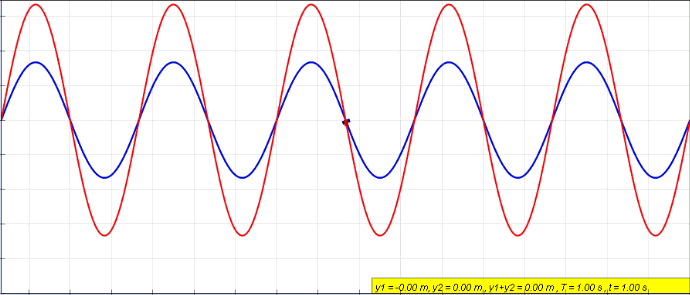
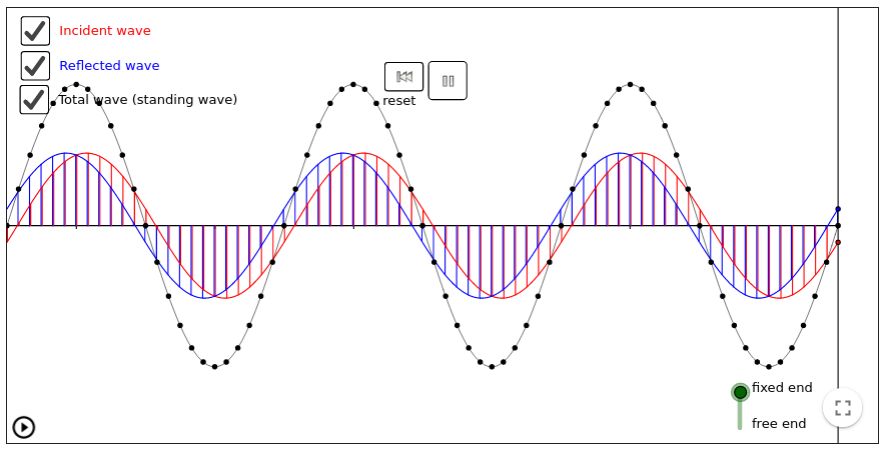
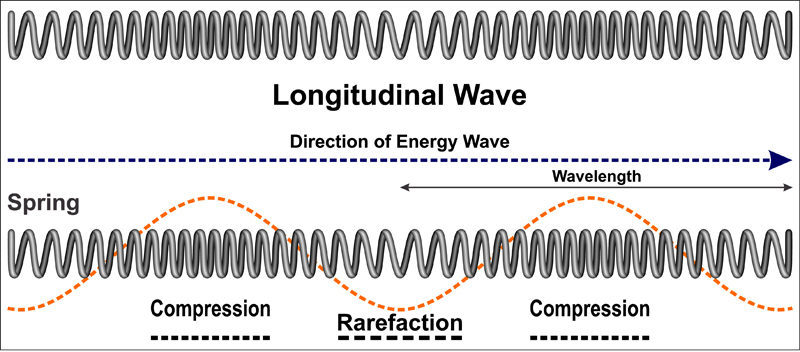
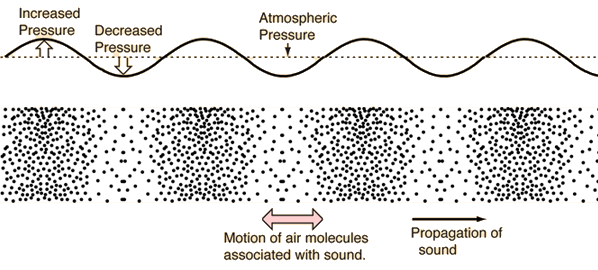
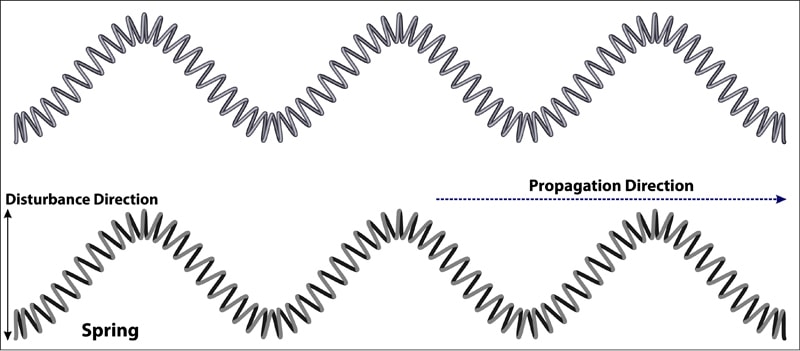
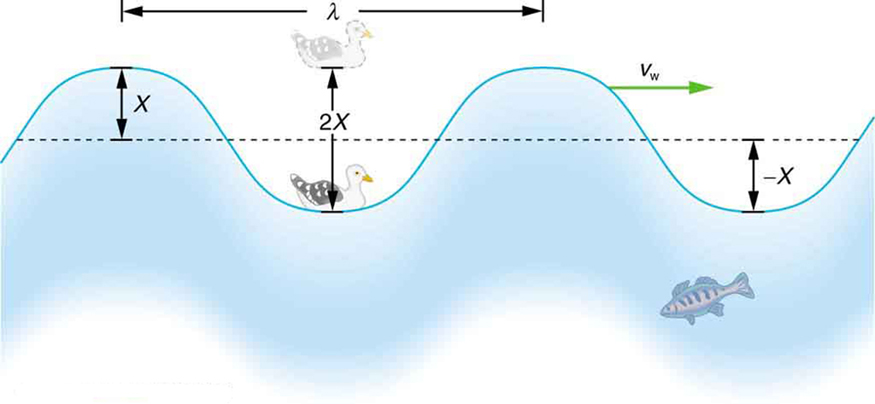
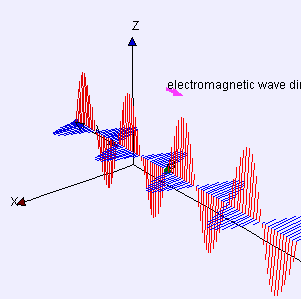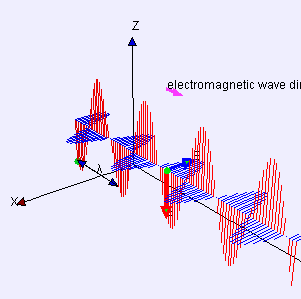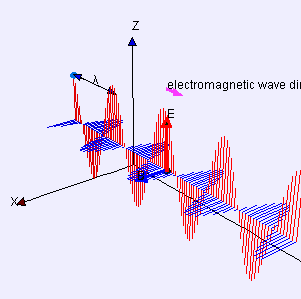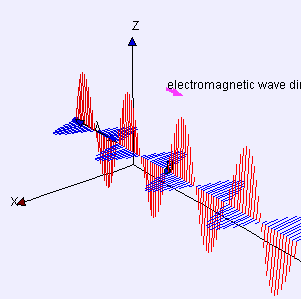
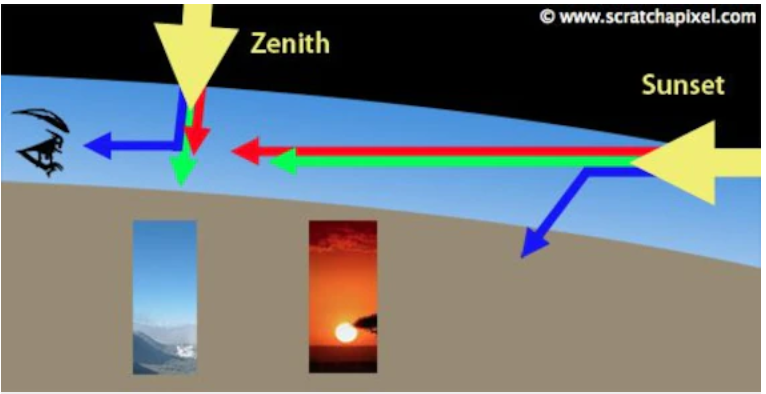
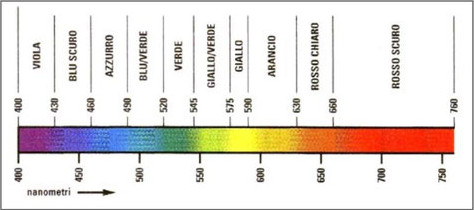
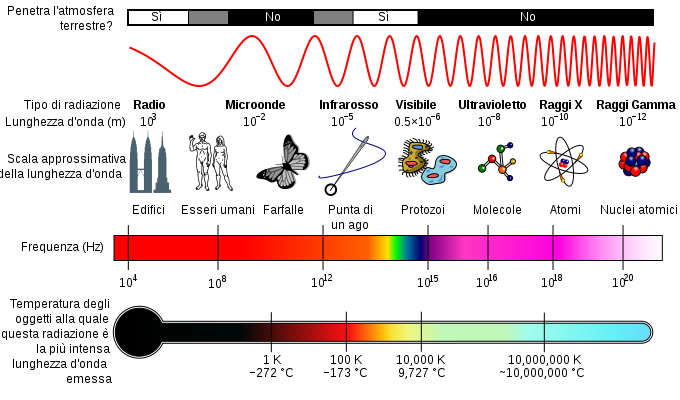
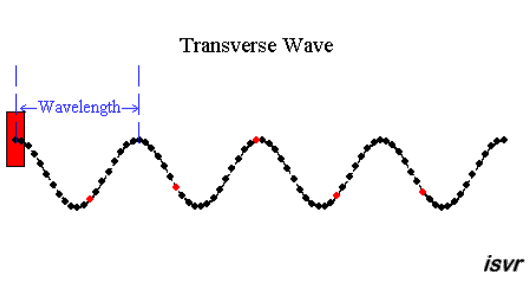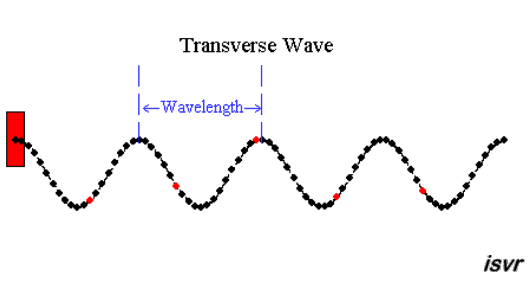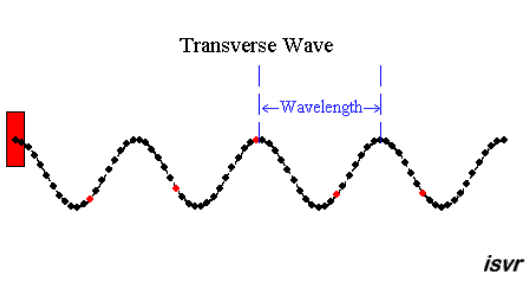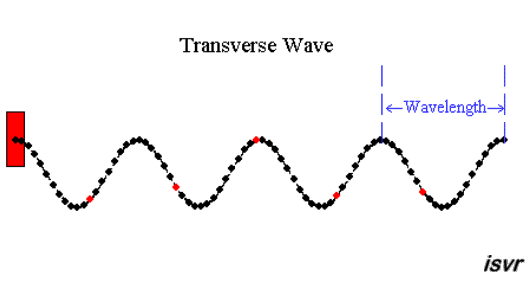
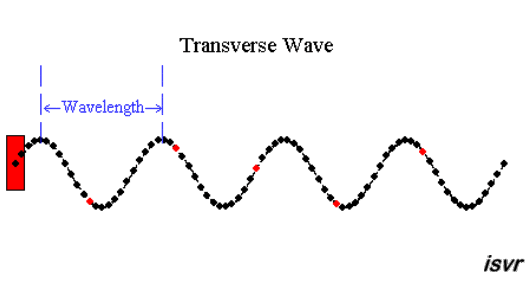
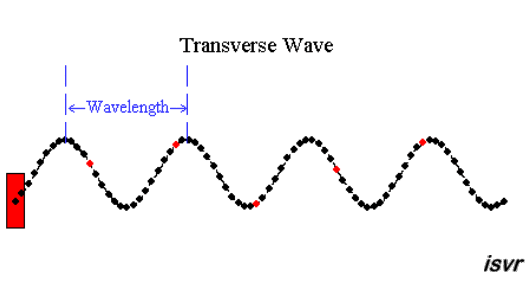
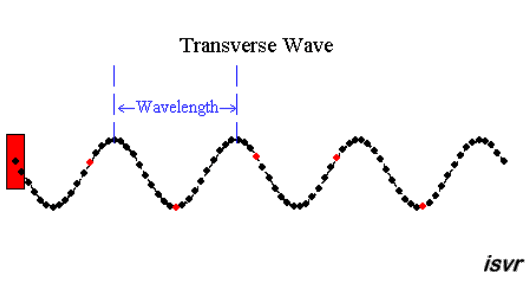
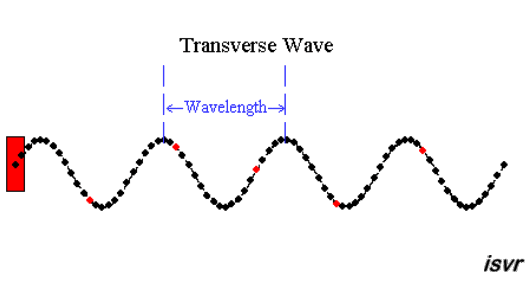
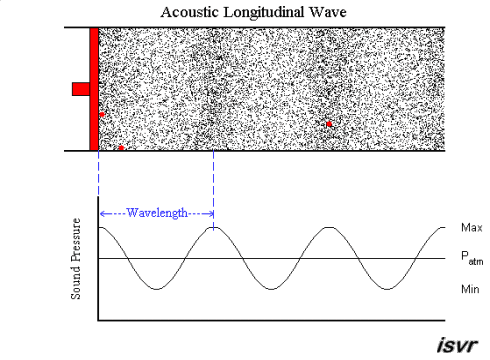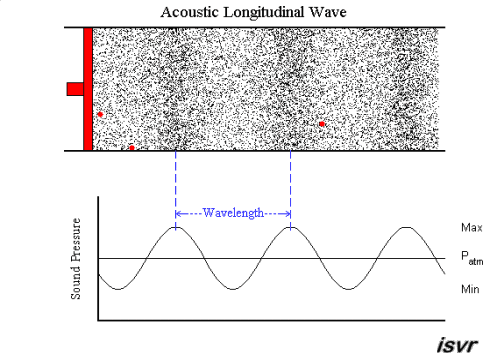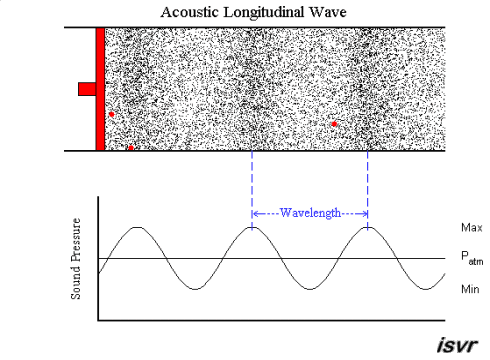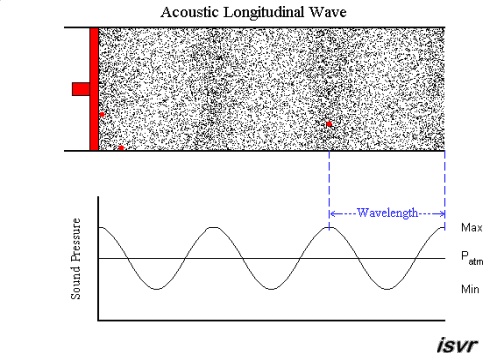
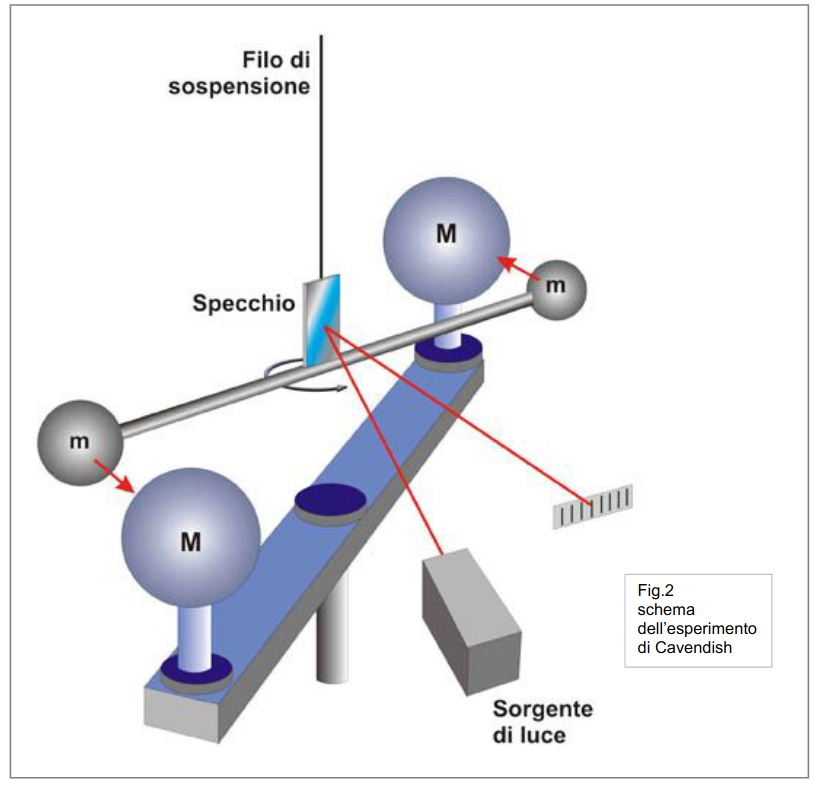
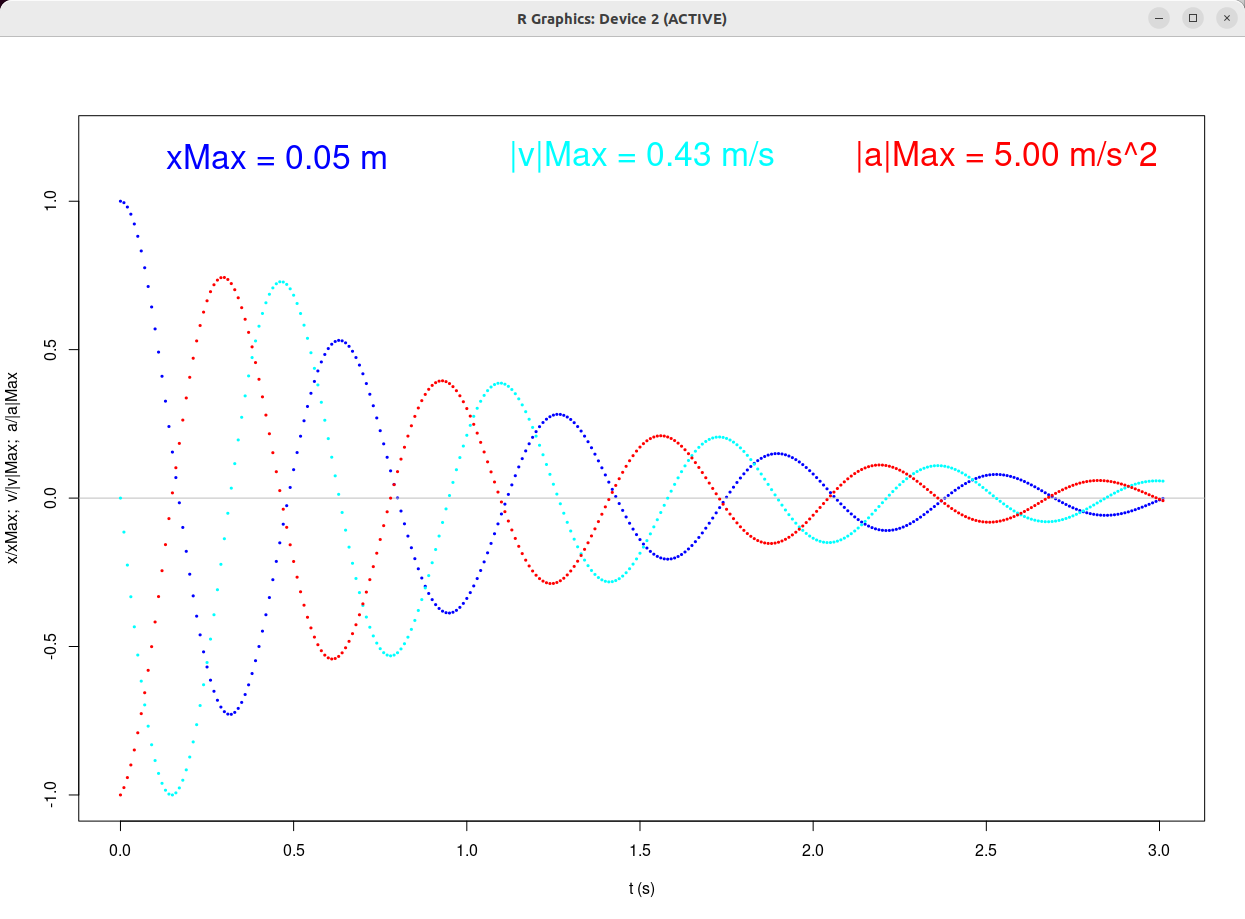
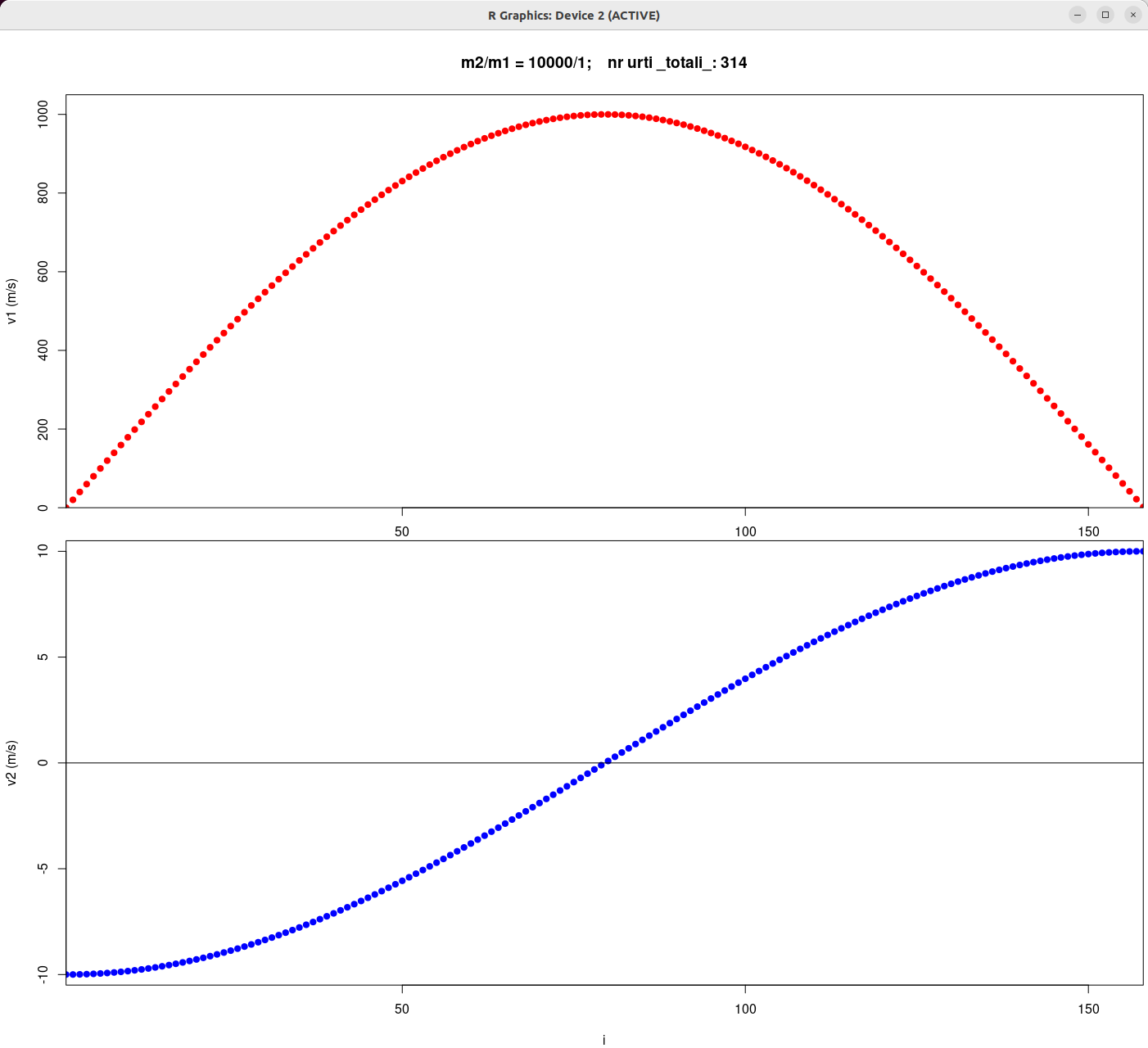
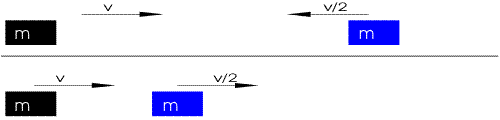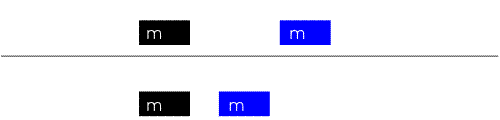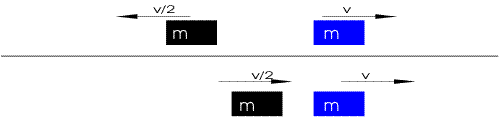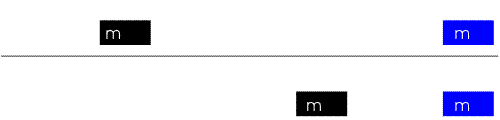
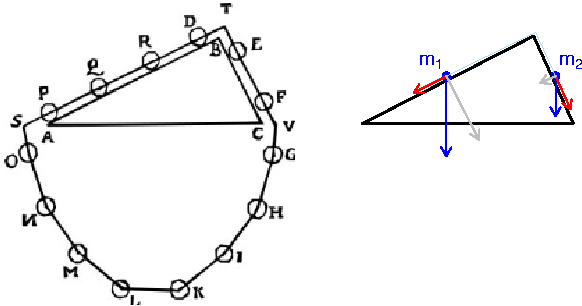
"è un pendolo con una grande forza"		"due corpi ... si respingono con forze che sono proporzionali alla forza che avevano quando si sono incontrati"

• al livello del pavimento;
• al livello del piano della cattedra;
• al livello del soffito.

(Distanza dal centro della Terra in unità del raggio terrestre)

"δός μοι ποῦ στῶ καὶ κινῶ τὴν γήν."
 

 
[  Da Wikipedia: si notino i rapporti di moltiplicazione e gli spostamenti degli estremi ]

• foto dell'uovo: uovo_polistirolo.jpeg
• script R: analisi_uovo.R
  [richiede il pacchetto magick (o simili) per importare la foto — cercare in rete]
  → emulare in Python.

[ Da Wikipedia. Attenzione: i tre 'c' sono numericamente diversi, come si evince dalle diverse pendenze,
mentre i vari λ non sono calori latenti, bensì calori latenti specifici (vedi e.g. 'SLH' in en.wikipedia) ]

• Standard interpolating thermometers and their ranges
• Defining points

• Script R, da provare a convertire in Python: funzioni_sinusoidali.R
  (per capire il motivo delle fasi +π/2 e +π si veda la Lezione nr. 14).
• Provare a visualizzare come le curve blu siano proporzionali^(*) alle derivate rispetto al tempo di quelle nere
  e quelle rosse siano proporzionali^(*) alle derivate rispetto al tempo di quelle blu!

   

                   

• Forza peso
• Forza peso, reazione vincolare e forza totale
• velocità e accelerazione

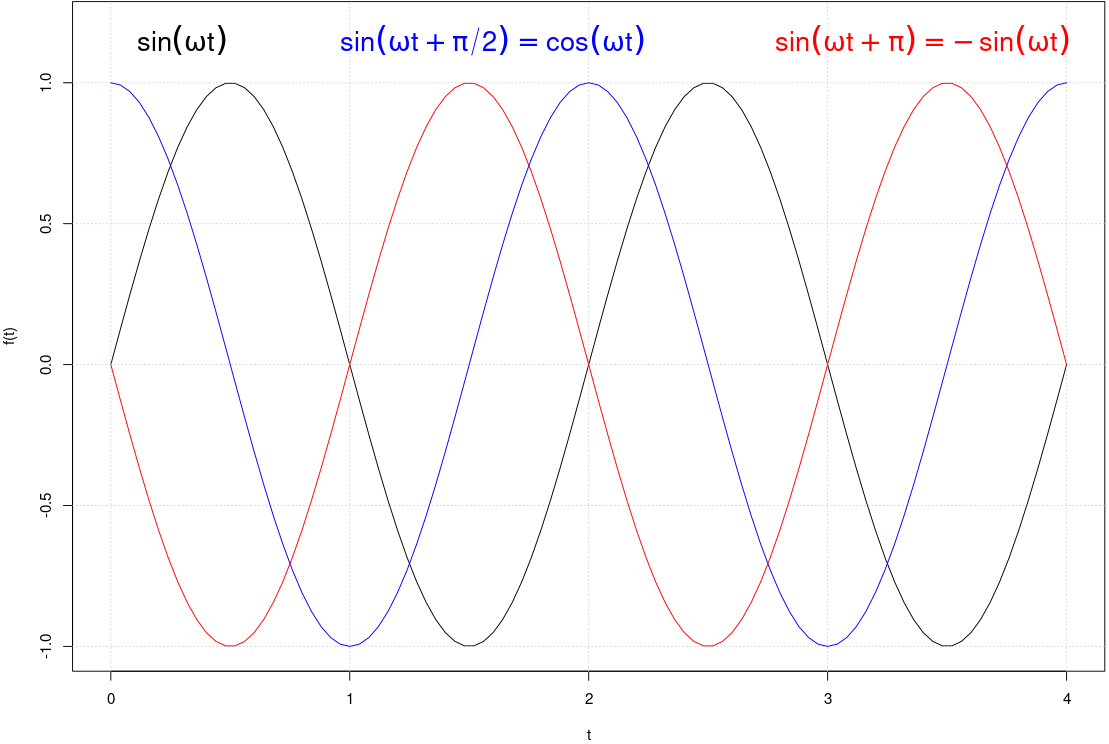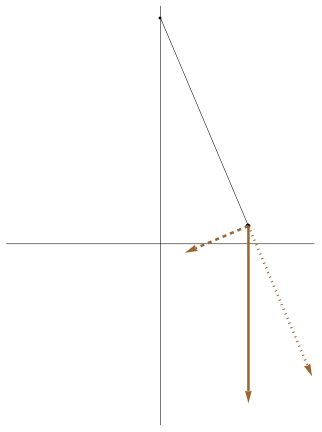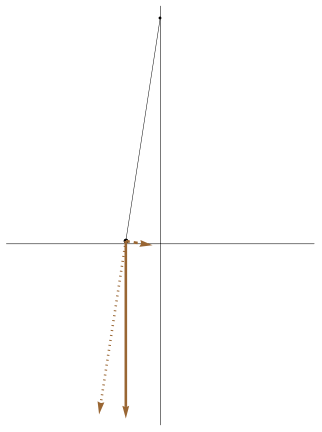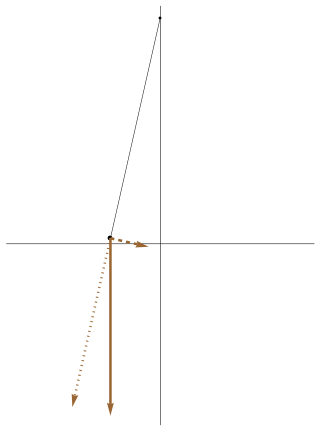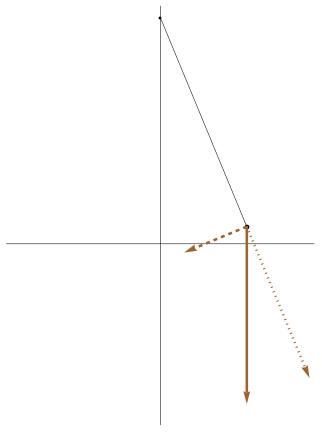
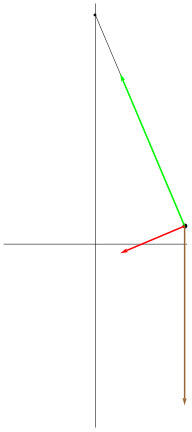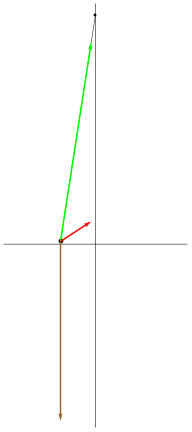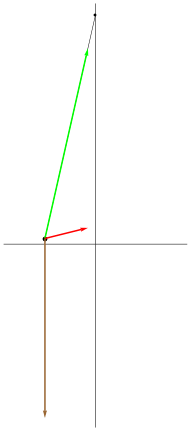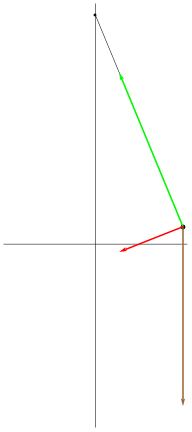
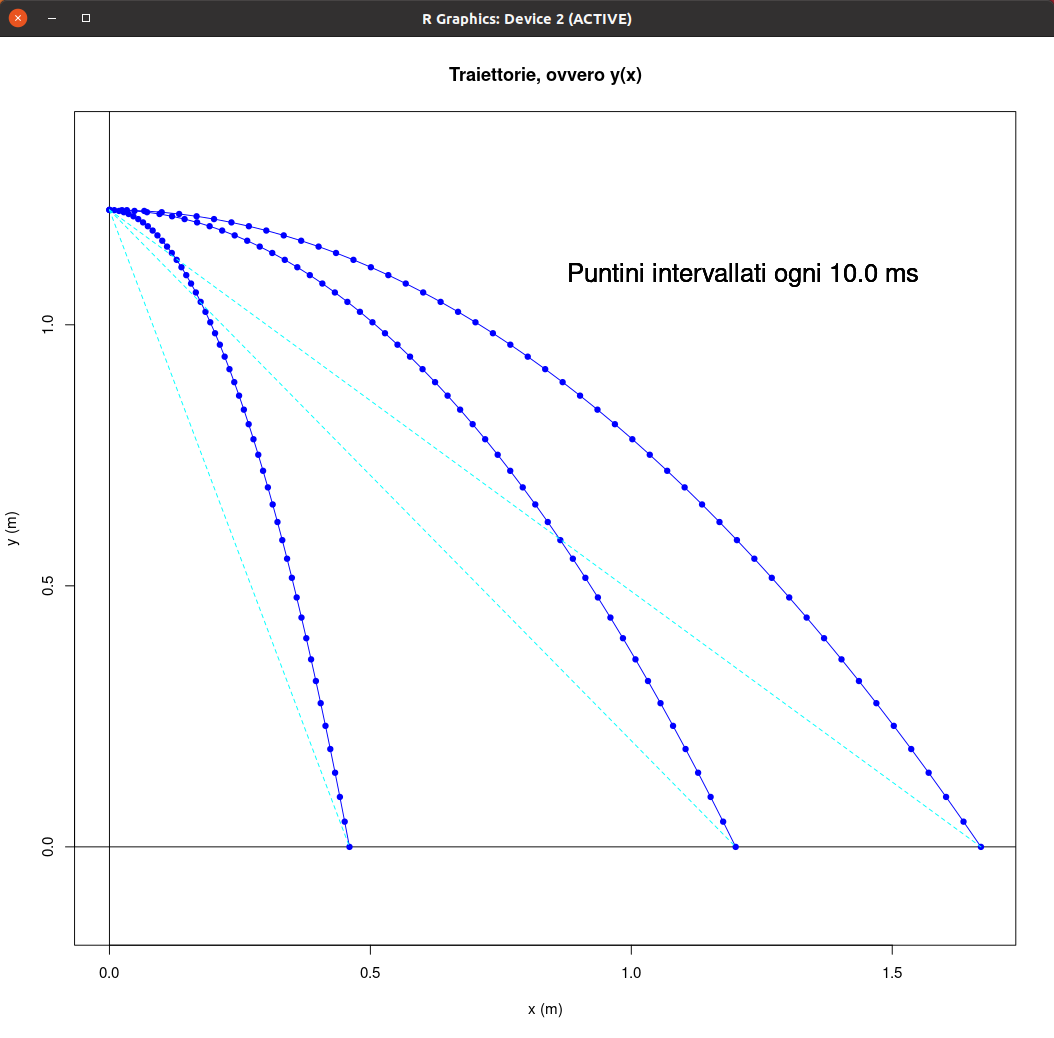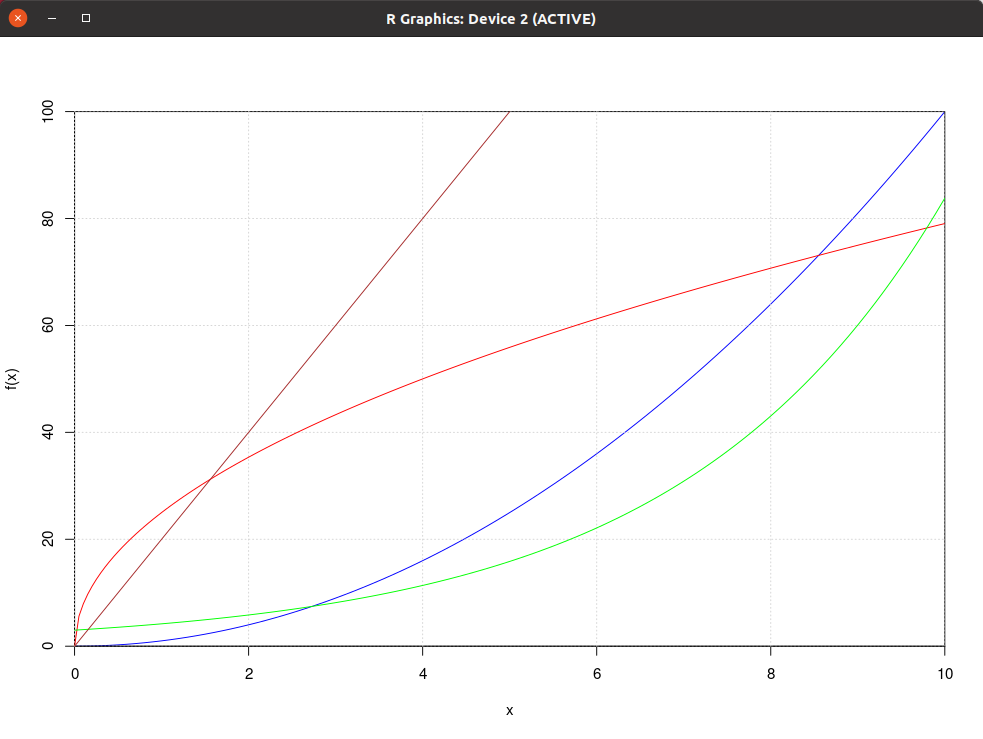
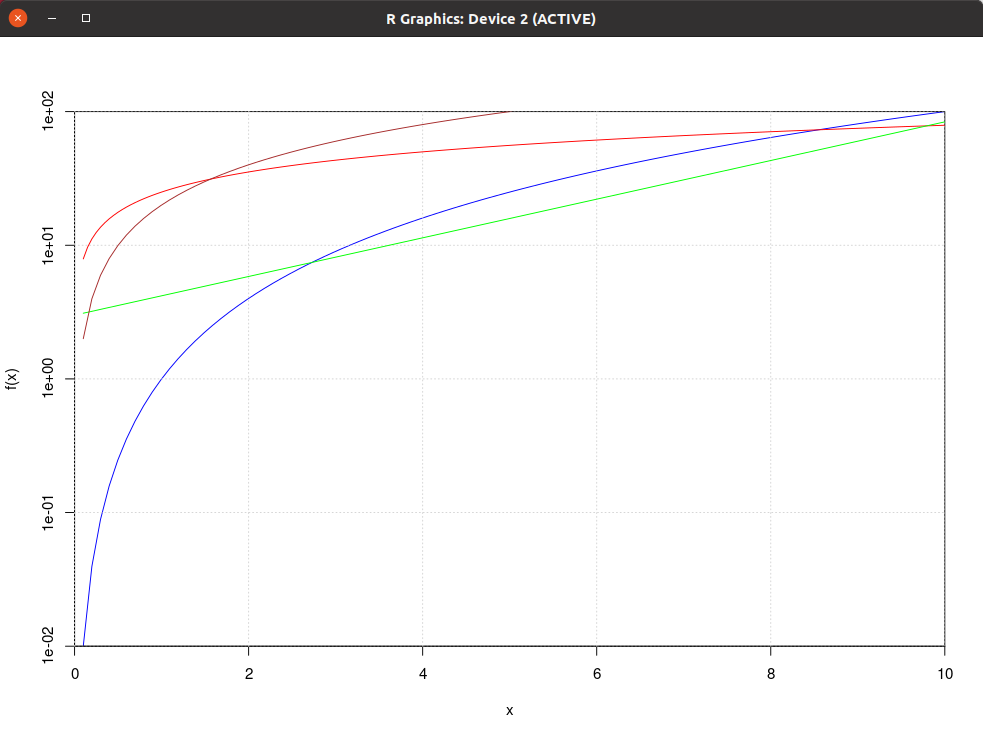
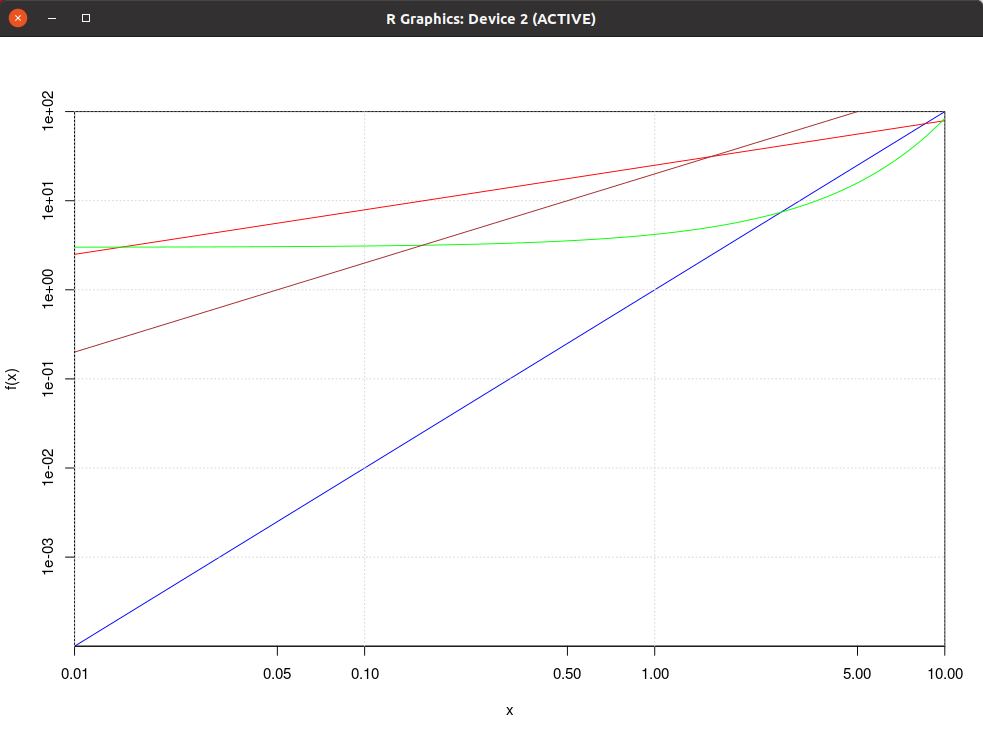
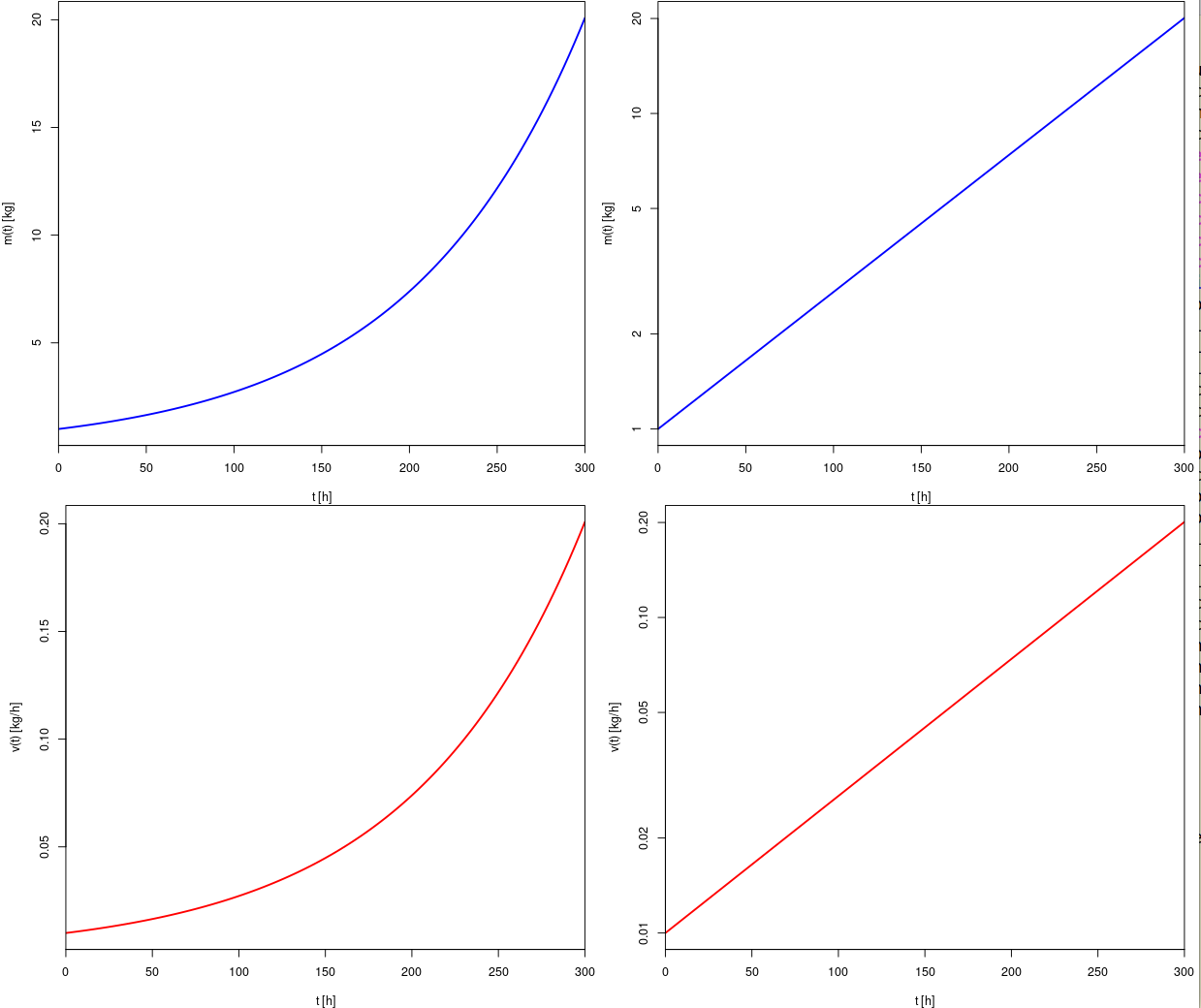
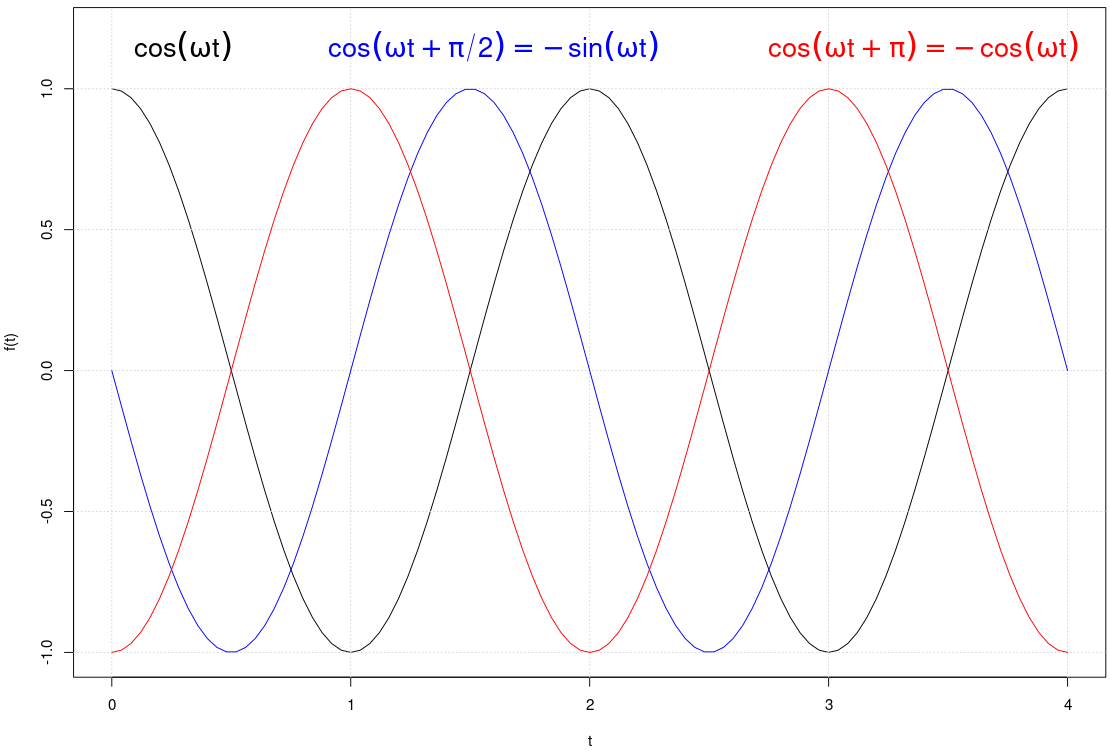
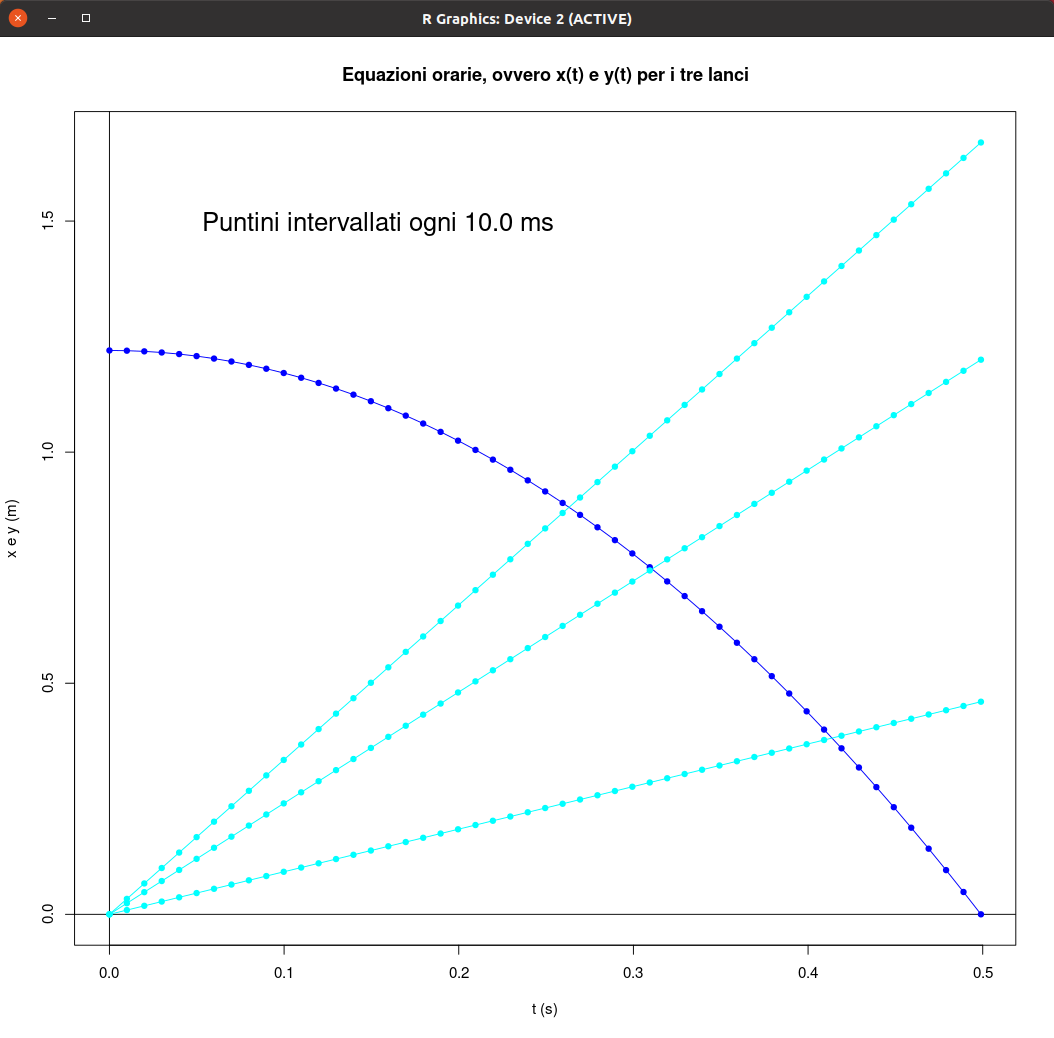
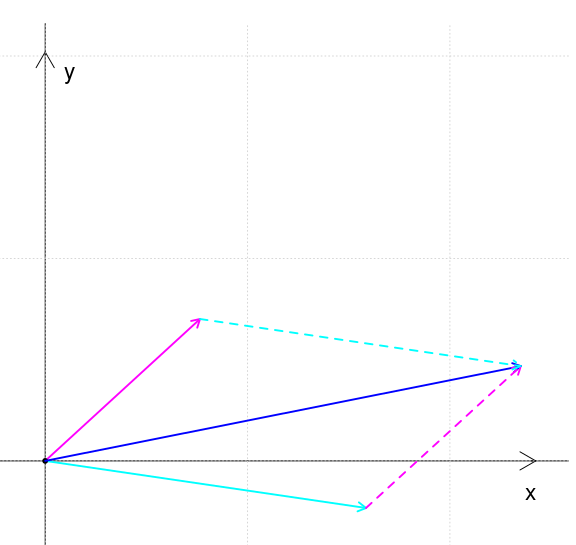
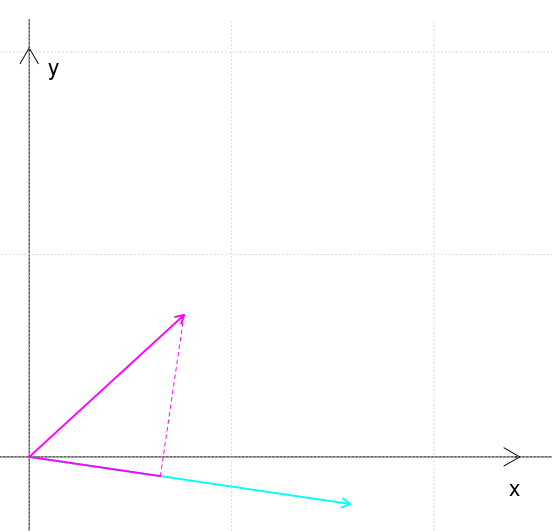
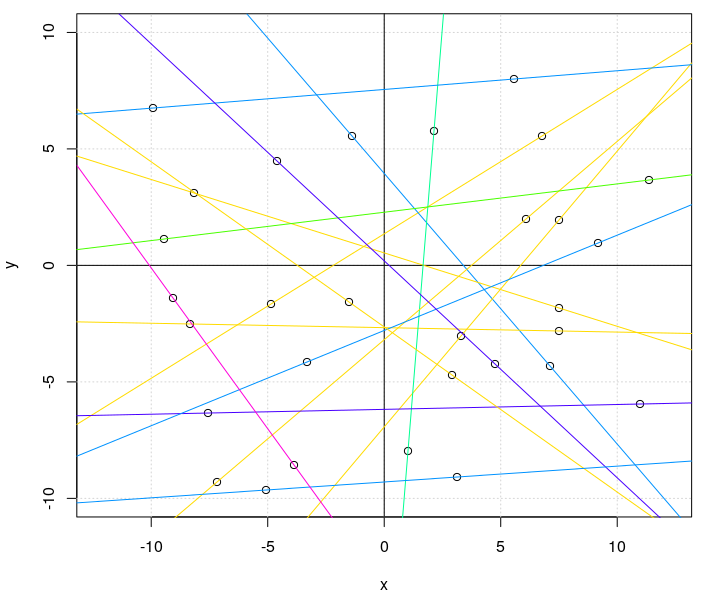
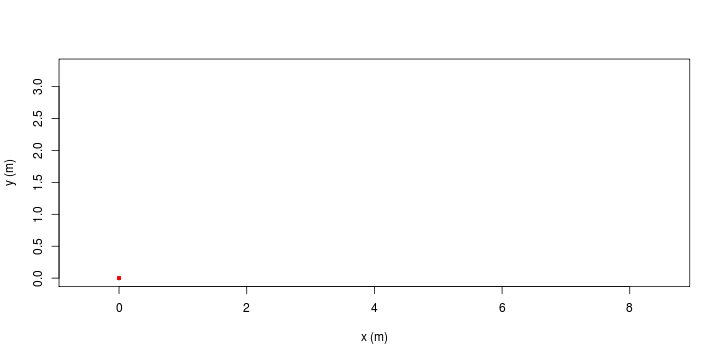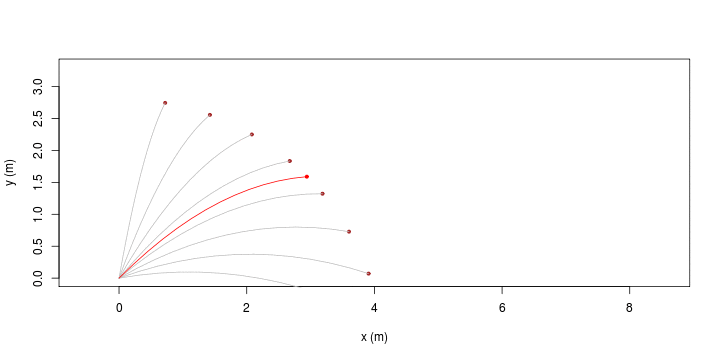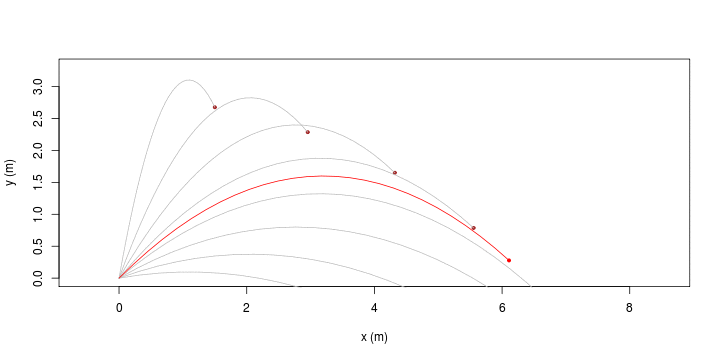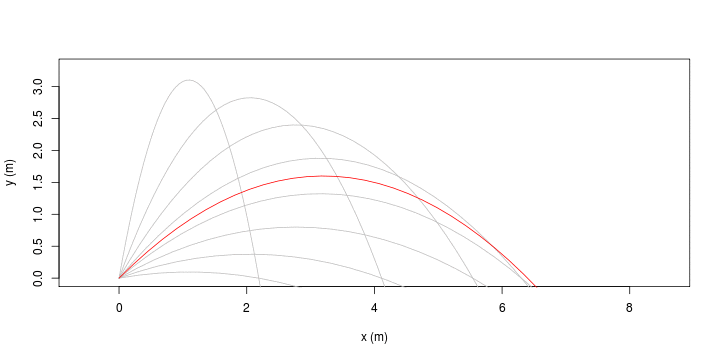
Equazioni orarie, ovvero x(t) e y(t)		Traiettorie, ovvero y(x)

Esperimento di Cavendish e 'misura della massa della Terra'

Eratostene e la misura della circonferenza terrestre

 
 

Terza legge di Keplero applicata ai pianeti del Sistema Solare (immagine da Wiki)

• Riconoscete le curiose scale?
• Quindi di che tipo di andamento si tratta?
• Sapreste ricavare la legge che lega il semiasse maggiore al periodo?
  (Si prendano ad esempio Terra e Saturno, i cui valori sono facilmente rileggibili dal grafico.)
• Per allenarsi ad usare le carte logaritmiche si confrontino i punti del plot con i valori riportati in dati_pianeti.txt (da nasa.gov)
  pronti ad essere usati in R (pianeti_overview.R e pianeti_log.R)
  → importare opportunamente in Python.

[ Colpo d'occhio su alcuni parametri orbitali (da Wikipedia) − Nota: le orbite reali non sono coplanari!^(*) ]

[ Rotazione della Terra e di un satellite geostazionario (da Wikipedia − vedi anche qui) ]

• prodotto_scalare_2D.R

• Script R: moto_circ_unif.R
• Provare a cambiare i parametri, in particolare T0
  (si notino i fattori di scala per rappresentare i vettori 'v' e 'a',
  anche perché rappresentarli nel piano (x,y) è una mostruosità
  → si pensi invece a dei layer grafici sovrapposti)
• Provare a 'tradurlo' in Python, arrangiandosi per le librerie di grafica
  (si tenga conto che in R gli indici dei vettori cominciano da 1)

• giri compiuti (→ da cui segue la velocità di rotazione: → giri/s → frequenza ν);
• spazio percorso (→ da cui segue la 'velocità lungo la circonferenza → v);
• angolo percorso (→ da cui segue la velocità angolare: → rad/s → pulsazione ω).

 

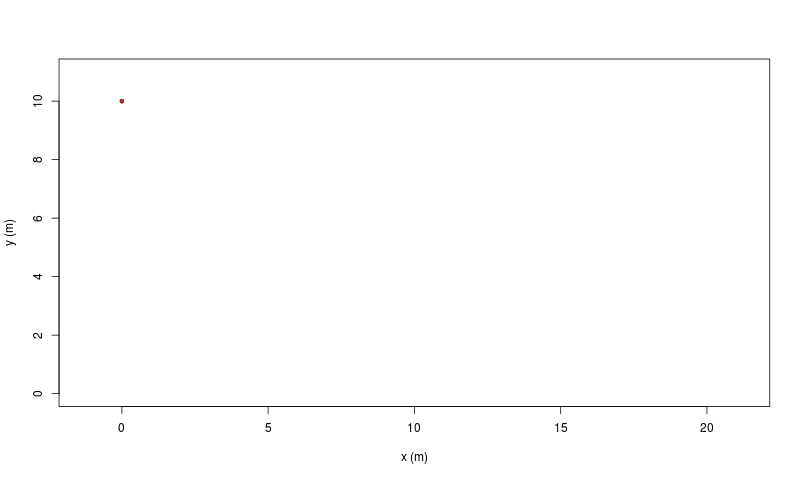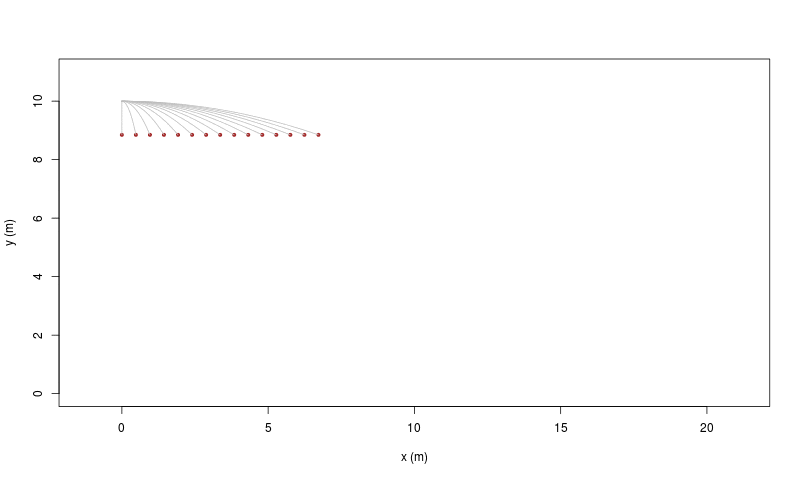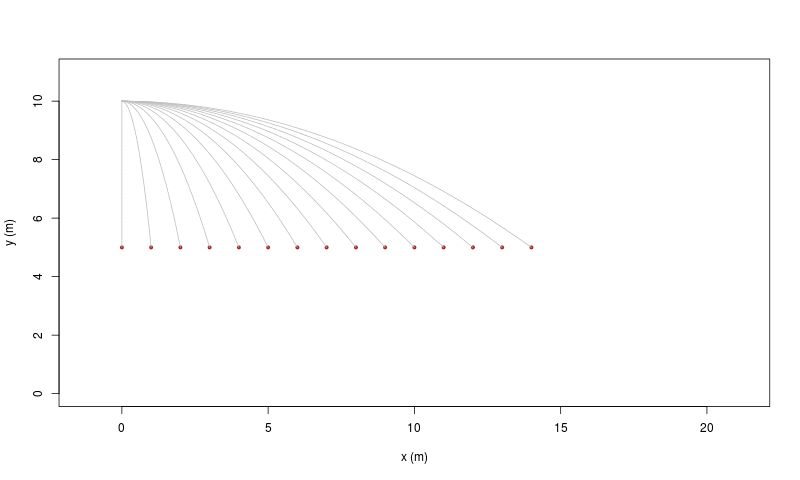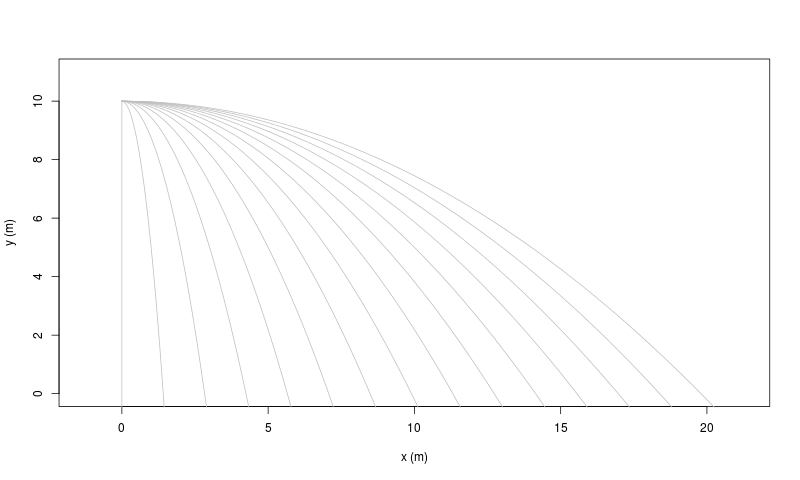
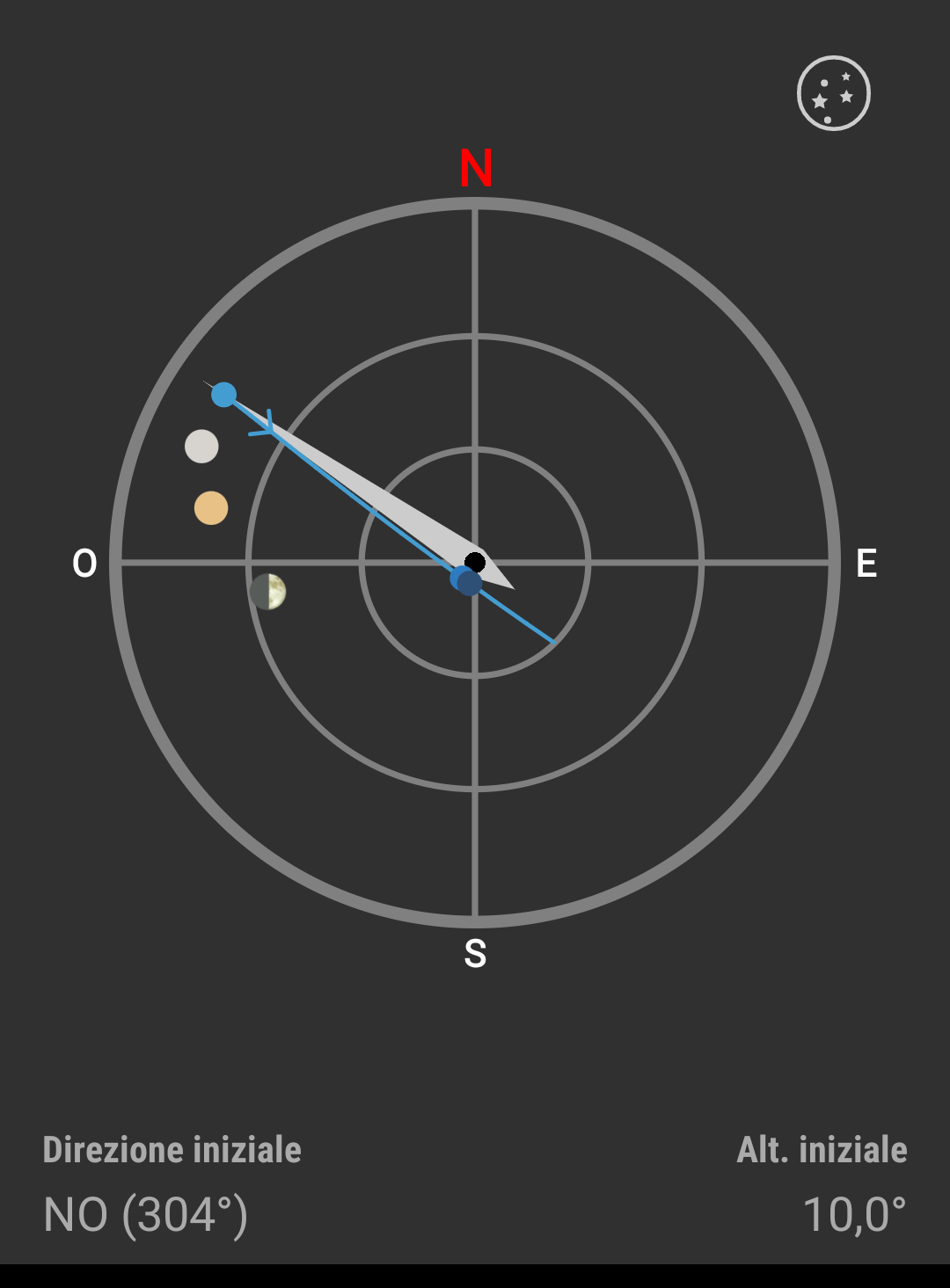
16 marzo		17 marzo
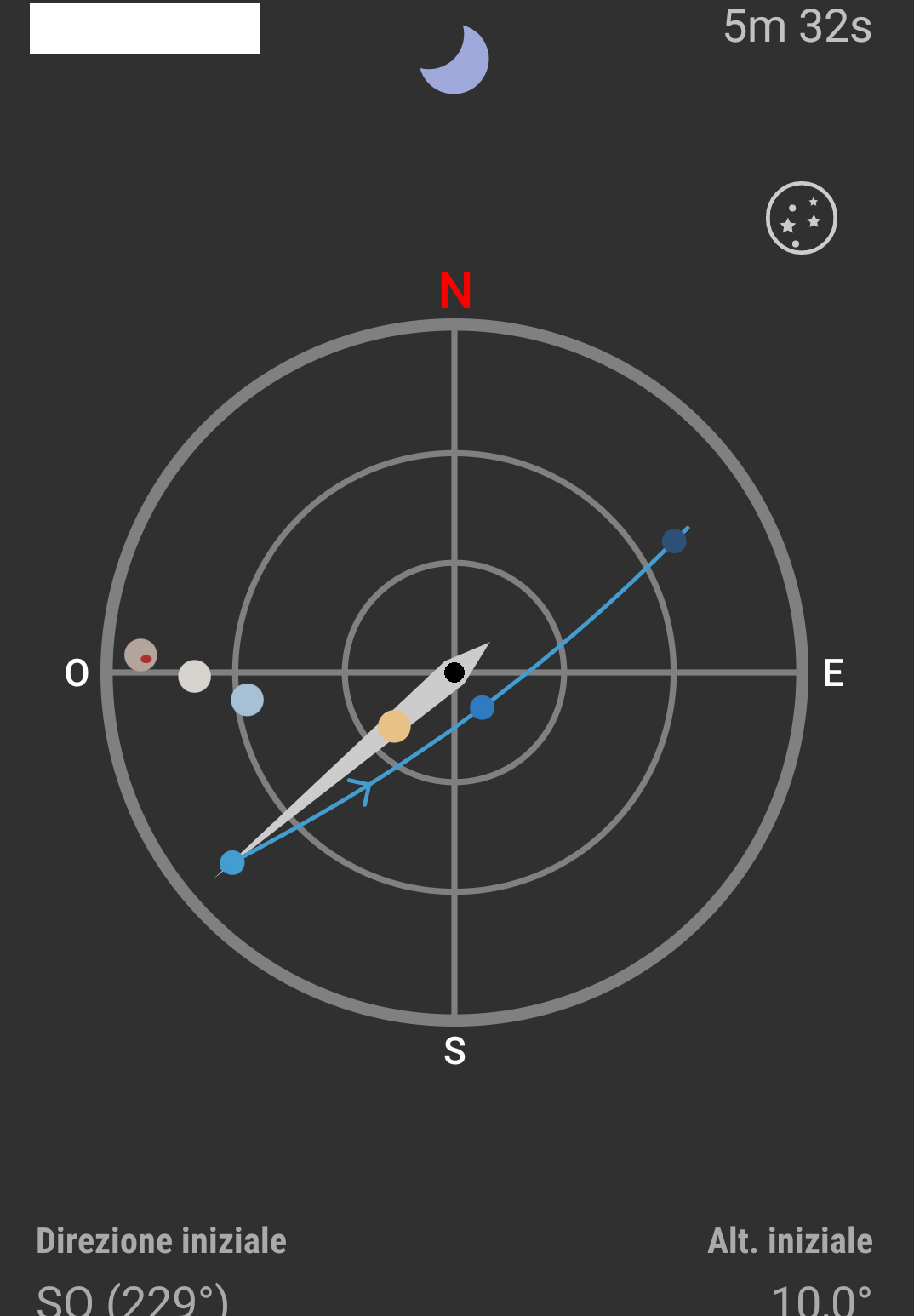		Magnitudine (massima) -4.7 !!

• oggetto in ipotetica orbita radente (puntino nero)
• oggetti oscillanti dentro due (altrettanto ipotetici) pozzi per il centro della Terra (blu e rosso)

 
[ Dai Principia di Newton ]

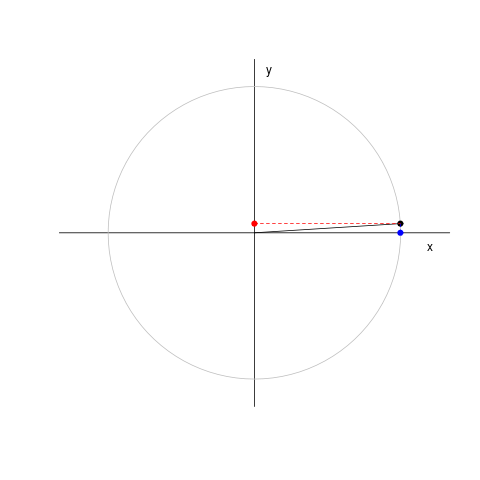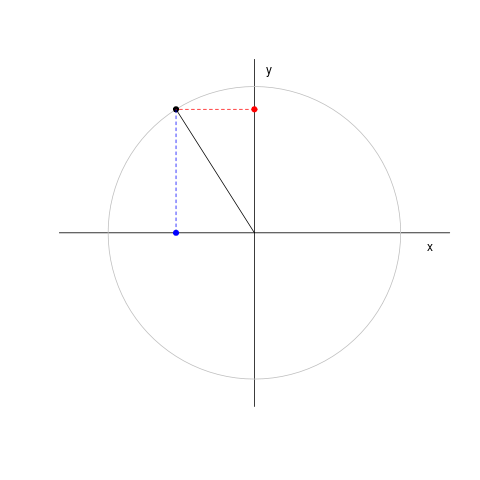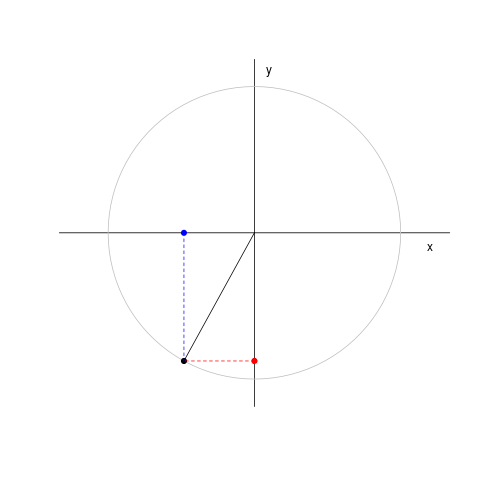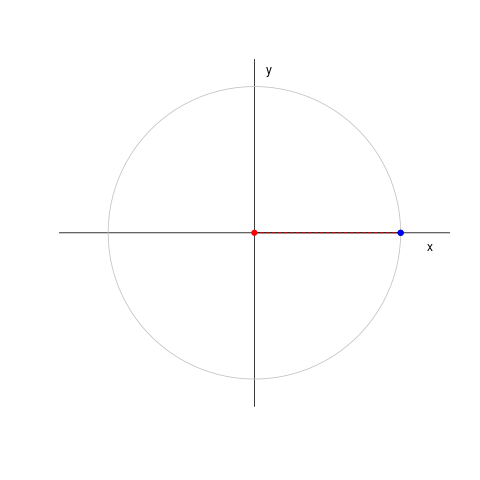
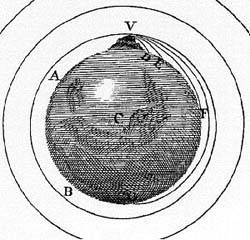
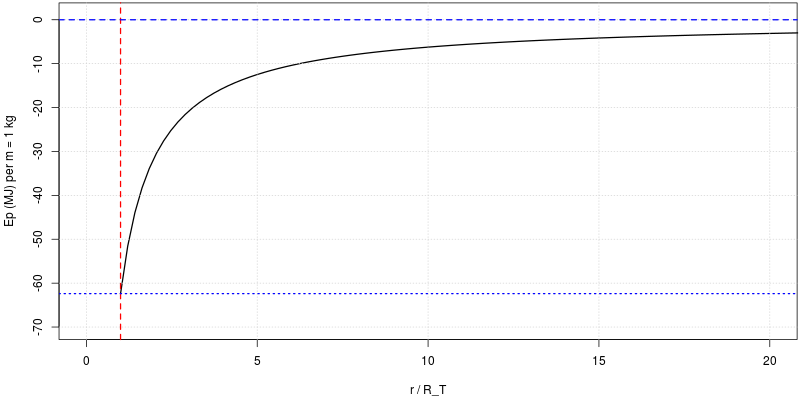
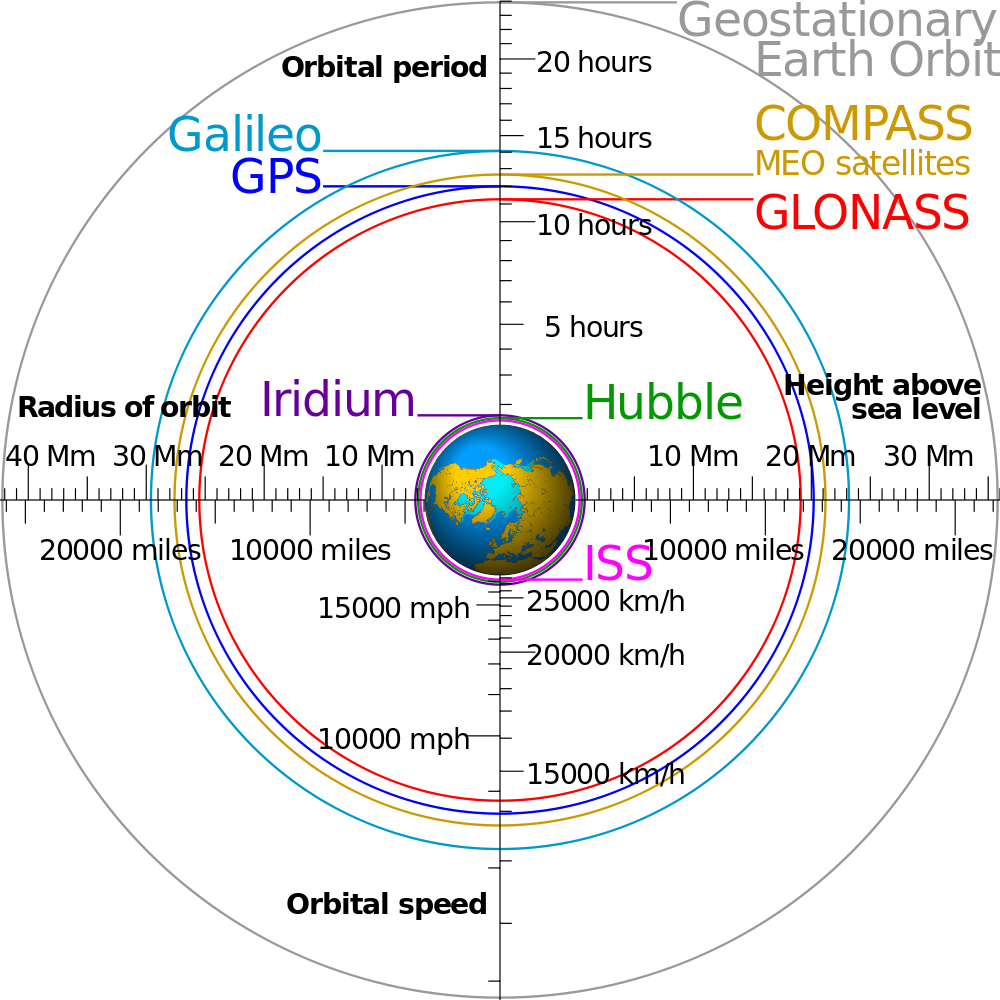
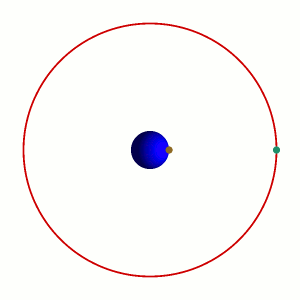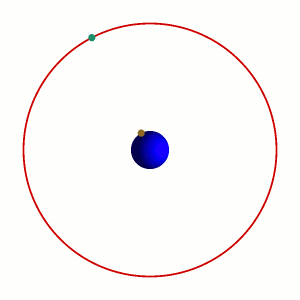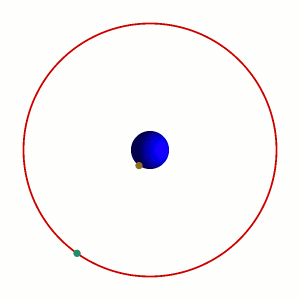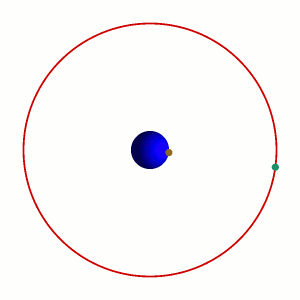
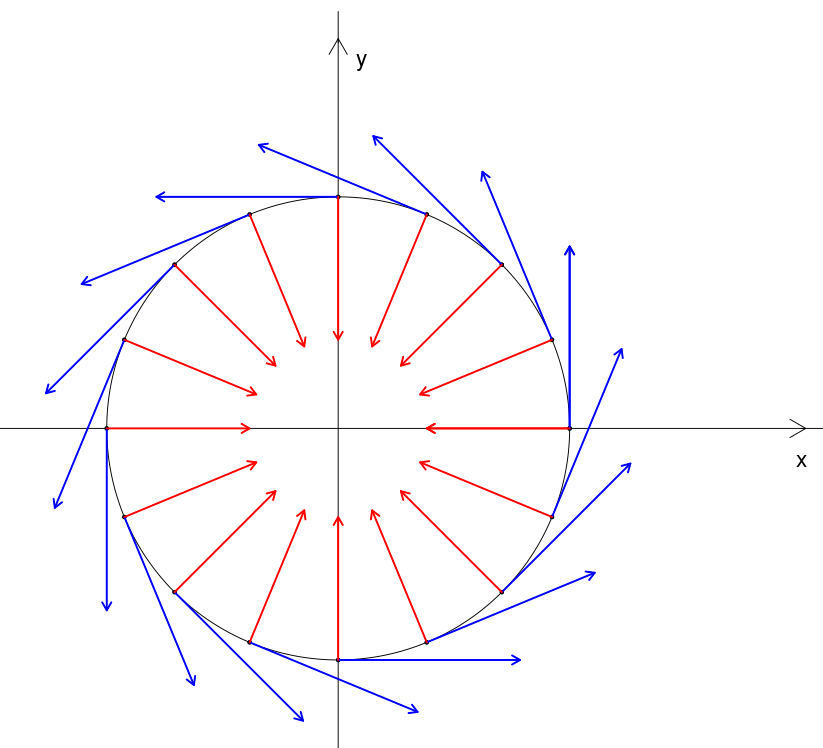
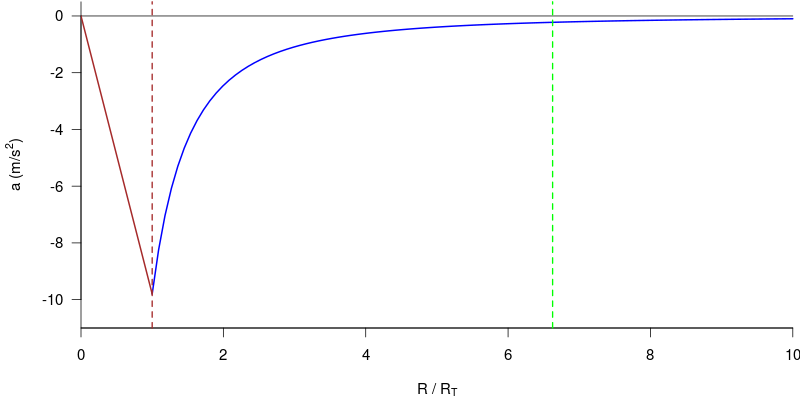
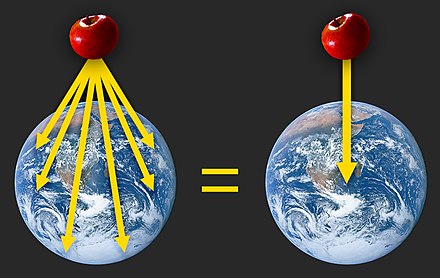
Il cosiddetto 'cannone di Newton' è un esperimento concettuale per far capire che le mele che cascano e la luna che gira derivano dalle stessi leggi della Fisica.

• Un'animazione a rallentatore (su piccole distanze).
• Simulazione interattiva con possibilità di scegliere la velocità iniziale.

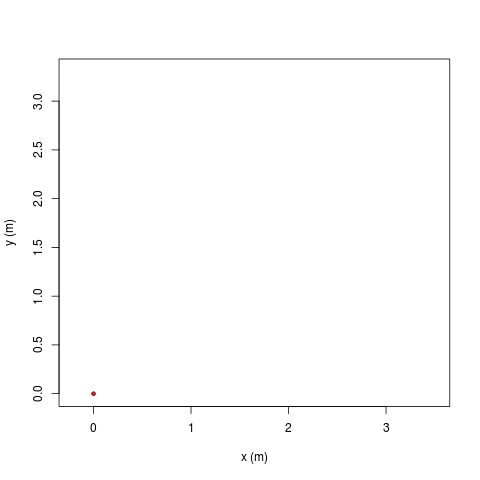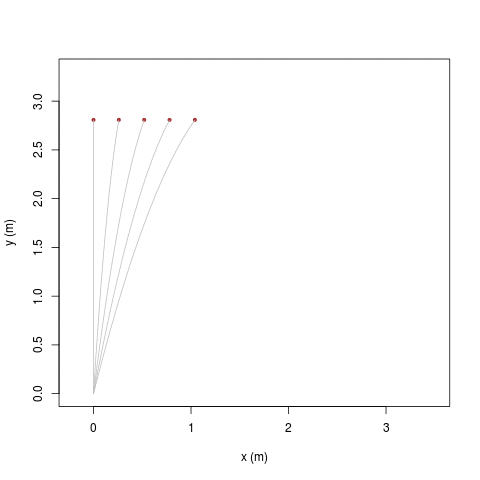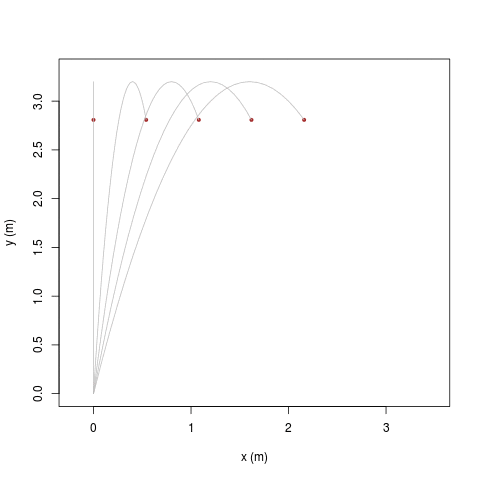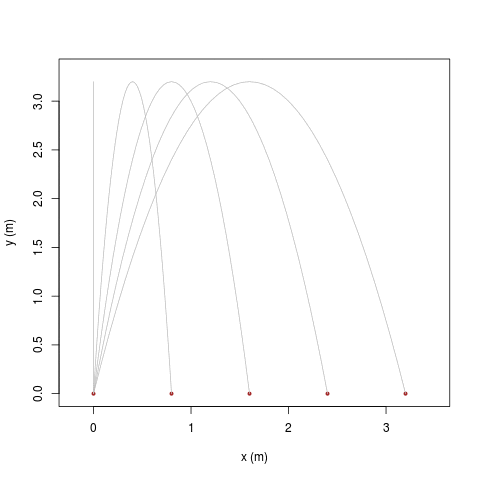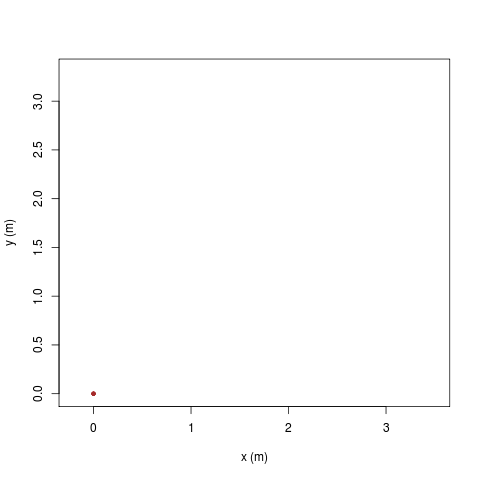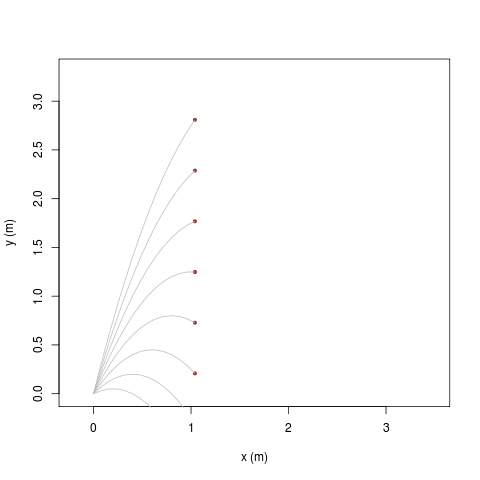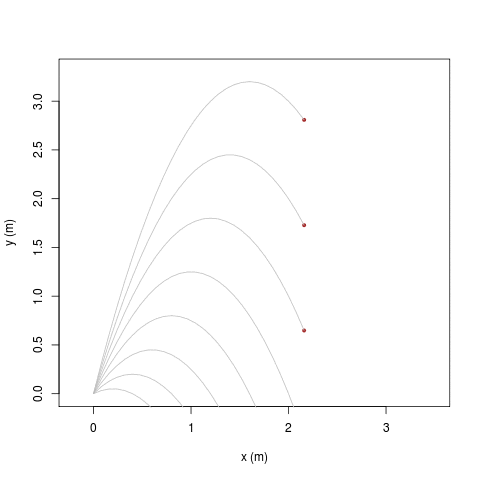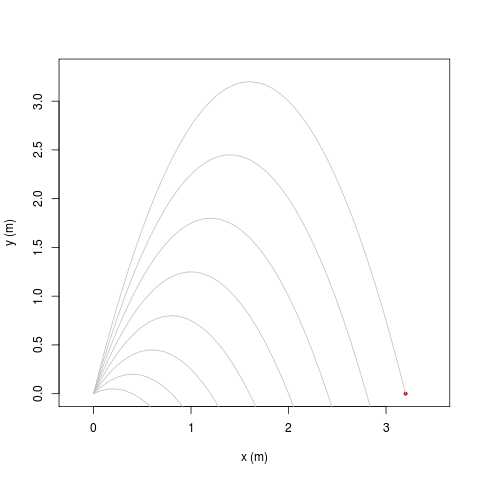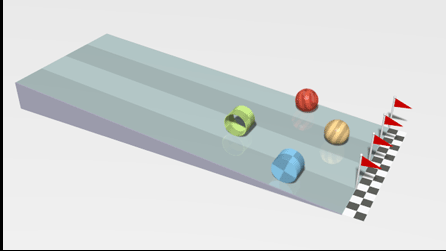
[ stessa vy0;   diverse vx0 ]	[ stessa vx0;   diverse vy0 ]

 

[Video]

• A sinistra: la pressione dipende solo dalla quota;
• A destra: consequenza del Principio di Pascal (non ancora visto a lezione).

Paradosso idrostatico La pressione dipende solo dal livello di acqua
e non dalla quantità d'acqua (o altro fluido) contenuto nel recipiente.
→ Talmente controintuitico da essere noto come

• Fisica del paracadutista: video su YouTube con ottima spiegazione dei contributi della forza peso e di quella di resistenza dell'aria (ed inizialmente anche della portanza dell'aereo, per finire con quella del terreno).
• Caduta dei gravi in aria e nel vuoto: video su YouTube della classica esperienza dimostrativa della piuma e del pezzettino di ferro.
• Caduta di martello e piuma sulla Luna video su YouTube dell'esperimento eseguito dall'equipaggio dell'Apollo 15 (per ulteriori dettagli vedi qui o qui)
• Il lancio di Felix Baumgartner
  • youtube (riassunto in 90s).
    Esercizio Dagli ultimi secondi del filmato provare a stimare la velocità di arrivo al suolo.

• campo gravitazionale (in unità naturali N/kg, formalmente equivalenti a m/s²);
• Forza agente su una massa di 1 kg a quella distanza (in tal caso espressa in N).

   

   

• cercare di capire la 'reazione uguale e contraria alla spinta di Archimede sul polistirolo';
• e che la cosa non cambia se il polistirolo è poggiato direttamente sulla bilancia
  (ma di questo ci si convince meglio quando togliamo (quasi) completamente l'aria da sotto un oggetto!)

• spezzate per guidate l'occhio;
• funzioni ottenute dalla linearizzazione.

• Si vede ancora la parte 'retroilluminata' dalla Terra.
• A che distanza si trova, approssimativamente, il palazzo sotto la luna dal punto dove è stata scattata la foto?
• Come mai la luna sembra schiacciata?

[ Vedi @dennisstever su Instagram, post del 28/11/2018 ]

 
 
 
[ Ma può essere più utile memorizzare i reciproci degli angoli espressi in radianti! ]
[ E, comunque, le dimensioni angolari variano da persona a persona ]

• Diametro angolare (Wiki)
• Angular diameter (Wiki inglese) (formula esatta, ma irrilevante per piccoli angoli)
  → Interessante la variazione di angolare per i diversi corpi celesti (si noti Venere!)

(Cliccare sopra per vedere l'intera foto — copia locale)

• in questo caso l'oggetto di riferimento è, al posto del pollice, il Sole;
• ma non è necessario ricorrere alla sua grandezza e alla distanza da noi.
  Si può far invece uso del suo diametro angolare, che, per il nostro scopo, possiamo prendere pari a 32', ovvero circa uguale a mezzo grado.
  (Il resto è un esercizio/ripasso di trigonometria.)
• E la grandezza del Cupolone? → Arrangiarsi!

• Nota: i segmenti fra un punto sperimentale e l'altro servono solo 'a guidare l'occhio' (to guide the eye)
  e non hanno alcun significato statistico/inferenziale!
• Che leggi seguono (idealmente) le quattro curve?
  (Tali leggi non sono seguite esattamente a causa di errori sperimentali.)
  → Per trovare tali leggi bisogna ragionare sulle formule che danno il volume della parte affondata in funzione dell'affondamento.
  → Vedi esercizi sugli integrali.

[Animazione, per capire meglio l'integrale.]

• larghetta pollice (a metà unghia): 2.2 cm;
• distanza 'occhio'-pollice: 59 cm;
• per il terzo dato... arrangiarsi.

• In generale un integrale è una somma di infiniti elementi infinitesimi
  e non un'area (è un'area solo se gli elementi infinitesimi sono essi stessi aree).
• In Fisica (e nelle Scienze in genere) gli integrali hanno in genere delle dimensioni fisiche
  e il risultato va quindi riportato con le corrette unità di misura
  ↠ il solo valore numerico non significa niente (a parte i rari casi in cui il risultato non sia un 'numero puro').

• l'indicazione di livello è fornita solo al di sopra di una certa temperatura minima;
• se la temperatura del liquido è molto elevata, per conduzione la tazza si scalderà sufficientemente anche al di sopra del livello del liquido causando una sovrastima del livello.

Aria	Vuoto

           
 
[Archimede & Newton (3^th Principle) at work]