Dettagli delle lezioni
[Galleria di immagini e link associati]
- Lezione 1 (27/02, 2h)
-
- Informazioni (mooolto) generali sul corso
- Test di autovalutazione
(assolutamente anonimo!)
- Sarà riproposto nelle prossime lezione, dando però meno tempo
per le risposte:
→ si prega quindi di rivedersi le domande, discuterne eventualmente con gli altri, e appuntarsi su carta le risposte.
- Sarà riproposto nelle prossime lezione, dando però meno tempo
per le risposte:
- Filo conduttore delle prime lezioni:
Misure di densità
(dalla densità di piccoli oggetti alla densità di Terra, Sole e Luna).- Misura della massa mediante bilancia elettronica;
- Misura di volumi di oggetti approssimabili
(idealizzazione!)
a solidi regolari:
- cilindro;
- sfera;
- parallelepipedo;
- prisma a base triangolare (retto);
- cono.
- Misura di volumi di piccoli oggetti
dalla forma irregolare non solubili
in acqua mediante volume di acqua spostata
(sasso)
- innalzamento di livello di acqua in un recipiente dalla forma 'cilindrica' (almeno localmente):
- valutazione della massa del liquido spostato mediante bilancia.
- Effetto della spinta di Archimede dovuta all'aria: → rilevante per il polistirolo!
- definizione di densità
('massa su volume' o 'peso su volume'?) - spinta di Archimede;
- principio di azione e reazione (`terzo principio');
- sensibilità di uno strumento o di una
procedura di misura
("variazione di risposta su variazione di stimolo").
- Dati raccolti (si prega di controllare!):
(manca il diametro interno del vasetto!)
Compiti per casa [*]:- valuare le densità dei vari oggetti;
- nel caso del polistirolo riportare i valori
ottenuti
- trascurando la spinta di Archimede;
- tenendo conto della spinta di Archimede.
- Ingegnarsi a pensare come si potrebbe valutare il diametro interno del barattolo.
- Per chi ha fatto Fisica alle superiori:
→ rivedersi come esordiscono i libri di testo (primi capitoli).
- Lezione 2 (01/03, 2h)
-
- Chiarimenti sull'impostazione del corso
(non un bignamone di altri corsi 'standard'):
- impostazione problem solving;
- approccio model thinking all'analisi del mondo reale.
- Elementi di metrologia:
- Misure (o misurazioni — 'measurements' in inglese):
- dirette (ad es. misure di massa con bilancia o misure di dimensioni di oggetti(*) con righello/calibro);
- indirette (ad es. misure di volumi e di densità).
- le misure dirette effettuate 'per confronto' (ad es. righelli o bilance classiche a due bracci) rappresentano solo casi particolari;
- l'uso di modelli geometrici (idealizzati!) fa parte della modellizzazione.
- Principio di misura ('fisico', 'chimico', etc.),
con esempi nel caso di termometri:- dilatazione di corpi;
- variazione di proprietà elettriche o elettroniche;
- variazione dello spettro di radiazioni elettromagnetiche.
- Sensibilità (da non confondersi con la 'risoluzione'!):
→ indica (in modo quantitativo) quanto la variazione dello 'stimolo fisico' (es. di temperatura), In, fa variare il valore numerico Out che si 'legge' sullo strumento (ad es. innalzamento della colonnina di mercurio):
↠ dOut/dIn. - Interpolazione fra le tacche nella lettura
di strumenti analogici:
- sforzarsi di leggere al meglio;
- dipende dalle condizioni di lavoro e dagli oggetti da misurare;
- le regole 'scolatiche' dogmatiche di ±1 divisione o ±1/2 sono dovute a curiose propagazioni di errori concettuali nella didattica e vanno evitate.
- Misure (o misurazioni — 'measurements' in inglese):
- Escursus su radiazione solare (ci ritorneremo — è anche una questione di
educazione civica!), al quale siamo arrivati
parlando della temperatura (superficiale) del Sole, misurata
mediante lo spettro della 'luce' (→radiaz. E.M.)
- potenza sulla Terra:
- fuori dell'atmosfera: c.a 1.4 kW/m2;
- al suolo, giornata serena, su superficie ortogonale ai raggi solari: c.a 1.0 kW/m2.
- Problema storico di come mai il Sole emanasse così tanta energia
senza consumarsi:
→ fusioni nucleari (ovviamente fuori programma). - Semplici problemi a partire dal dato sull'irraggiamento
sulla Terra (fuori dell'atmosfera):
- valutare la potenza totale che arriva sul 'discho terrestre';
- valutare l'irraggiamento (kW/m2) su un corpo distante dal Sole il doppio della Terra;
- valutare l'irraggiamento (kW/m2) su Venere e su Marte;
- valutare l'irraggiamento totale del Sole (W);
- valutare l'irraggiamento per unità di superficie (kW/m2) dalla superficie del Sole;
- dal risultato ottenuto nel punto 4 e, facendo uso della famosa E = m c2, valutare la quantità di massa trasformata in energia ogni secondo all'interno del Sole a causa della fusione nucleare.
- potenza sulla Terra:
- Secondo test di autovalutazione.
- Misure delle variazioni del valore letto sulla
bilancia in funzione dell'affondamento controllato
di alcuni 'solidi regolari' (o assunti tali):
- foto della lavagna con i dati sperimentali;
- tabella di valori: misure_affondamenti.dat
- graficare i dati e cercare di capire la ragione dei quattro diversi andamenti empirici.
- Ricavarsi le formule del volume di
- cilindro;
- prisma;
- cono;
- sfera
[Promemoria]
- Chiarimenti sull'impostazione del corso
(non un bignamone di altri corsi 'standard'):
- Lezione 3 (02/03, 2h)
-
- Ancora su principio di misura: misura di 'masse'
(termine da chiarire).
- Sulla questione del 'principio di misura', si risolva il problema proposto nella Galleria di immagini
- Richiamo qualitativo alla forza di gravità a cui è soggetto un corpo sulla superficie terrestre.
- Misura della massa di una bottiglia
- senza aria all'interno → 'vuoto' (non assoluto);
- con aria
→ [Si noti il leggero aumento prima ancora di aprire il rubinetto → misura leggermente sottostimata]
→ Volume della bottiglia (misurato successivamente dal tecnico del Laboratorio): 980 mL.
Sul tema: - Principi di Newton della Meccanica.
In particolare: importanza della scrittura a = F/m (cominciamo con problemi 1D):- Cause → Effetto
- (F,m) → a
- a ∝ F
- a ∝ 1/m
- In particolare, la massa m che compare nel secondo principio è la massa inerziale.
- Chiarimenti sul terzo principio
→ da non confondere con due forze su un corpo che danno risultante nulla!
→ FA(B) = - FB(A) - Forza gravitazionale (altra Legge di Newton) fra
- due punti materiali
- sfera omogenea e punto materiale fuori di essa;
- due sfere omogenea.
(→ risposte alla domanda nr. 5 del secondo test, con l'83% di risposte errate.) - Forza di Newton fra masse e
Forza di Coulomb fra cariche elettriche
- stessa struttura formale;
- chiarisce il significato di massa gravitazionale come una 'specie di carica di massa';
- la grande differenza fra le due è
che, come noto,
- la forza di gravità è sempre attrattiva;
- la forza elettrica ('elettrostatica') può essere attrattiva o repulsiva a seconda del segno del prodotto delle cariche.
- Forze e campi:
- "forza diviso 'carica'" (sia elettrica che di massa).
- Sul doppio significato della ben nota 'g'
(sulla superficie terrestre)
- costante di proporzionalità che fra massa (gravitazionale!)
e forza:
→ è quindi un campo: g = 9.8 N/kg; - l'accelerazione di m si ottiene dalla seconda legge di Newton:
→ a = (m g) / m = g- accelerazione 'di caduta libera':
- 9.8 m/s2;
- 9.8 (m/s)/s;
- ... (km/h)/s (valutare il valore numerico come esercizio)
- accelerazione 'di caduta libera':
- costante di proporzionalità che fra massa (gravitazionale!)
e forza:
- Commenti sui quesiti
dei due test di valutazione (con chiarimenti
sulla scelta dei problemi, in nessun caso
con difficoltà tecniche di calcolo!),
in particolare, visto l'argomento della lezione di oggi, cosa succede alla forza peso del 'viaggiatore' nell'ipotetico Viaggio al centro della Terra?
(A proposito, rivedersi le coordinate geografiche di Roma.)- Alcuni problemi sono stati riproposti, con varianti;
- nuovo quesito, 'ispirato' a quello dello scioglimento
del ghiaccio:
→ 'incudine' su canotto e in fondo alla piscina:- provare a fare esperimento a casa facendo uso di piccoli recipienti.
↠ Si raccomanda- di mettersi in regola con i problemi in corso;
- di rivedere le risposte date ai quesiti
(e 'ravvedersi' in caso di risposte errate),
ma, seguendo l'avvertimento di Mafalda, senza tentare di 'imparare le risposte'.
- Ancora su principio di misura: misura di 'masse'
(termine da chiarire).
- Lezione 4 (06/03, 2h)
-
- Galleria di immagini e link associati
come ripasso di varie cose viste nelle prime lezioni, con varie precisazioni
↠ Si raccomanda di svolgere tempestivamente i problemi proposti
al fine di capire i concetti illustrati e prepararsi a quelli che seguiranno. - Misure di densità a partire dai dati raccolti in aula:
- Nota il diametro del cono+cilindro non era stato riportato a suo tempo sulla lavagna. Chi ha effettuato la misura afferma che esso era pari a 37 mm (o 37.0 mm mm? — misura effettuata con righello).
- Quali unità di misura utilizzare?
- Nessun obbligo di usare le unità di base del Sistema Internazione, ovvero, in questo caso, kg/m3;
- In molti casi pratici è preferibile usare opportuni multipli
o sottomultipli, al fine da rendere il risultato più
facilmente percettibile:
in questo caso g/dm3 (ovvero g/L).
- Importanza della spinta di Archimede nel caso del polistirolo:
per quanto riguarda la densità dell'aria, da cui tale spinta dipende, si poteva usare (tanto per avere un valore — vedi sotto)- il valore misurato (indirettamente) mediante l'esperimento in aula con la bottiglia inizialmente vuota;
- valore nominato trovato ad es. su Wikipedia,
- composizione dell'aria (e quindi dall'umidità);
- temperatura;
- pressione.
(Si approfitta per ricordare, se ce ne fosse bisogno, che sbagliando s'impara, da cui l'importanza di eseguire con prontezza i lavori proposti.) - Si ricorda che il volume del sasso è stato misurato
dall'alzamento di livello dell'acqua quando esso è affondato nel bicchiere
(e bel barattolo):
- Si può fare di meglio? (soprattutto alla luce della digressione
sulle cifre significative)
→ pensarci e venire con proposte.
- Si può fare di meglio? (soprattutto alla luce della digressione
sulle cifre significative)
- Come mai la densità dell'acqua è (quasi) esattamente
1 g/cm3, ovvero 1 kg/dm3, ovvero 1 kg/L?
Breve escursus sulla definizione del metro e del chilogrammo durante la Rivoluzione Francese.
→ Chi vuole approfondire può vedere qui (→ Why does the meter beat the second? — in particolare l'articolo su Progetto Alice). - Breve digressione sulle cifre significative:
- innanzitutto le cifre dopo la virgola non significano niente,
in quanto la virgola dipende dall'unità di misura usata, mentre il numero di cifre significative non dipende dall'unità di misura; - nelle misure dirette sforzarsi di leggere al meglio;
- nel caso di misure indirette, effettuate quindi effettuando
opportuni calcoli si usi un po' buonsenso,
aiutandosi anche dalle regolette empiriche illustrate a lezione per moltiplicazione/divisione e somma/differenza.(*) - Per dettagli si veda qui (→ par. 3.4 della dispensa Le basi del metodo sperimentale).
- Ovviamente, si raccomanda di (eventualmente) correggere i risultati numerici ottenuti per le misure di densità.
- Inoltre, alla luce di queste considerazioni, anche negli esercizi 'teorici', ovvero in quelli che non sono basati su dati sperimentali, si raccomanda di limitare a 2-3 il numero di cifre significative.
(*) → si provi a riottenere i risultati con il proprio linguaggio preferito. - innanzitutto le cifre dopo la virgola non significano niente,
- Volumi ottenuti come somma di infiniti volumetti infinitesimi
(→ 'integrale'):
- a lezione visto il caso della piramide;
- fare gli altri (chi non li avesse ancora fatti),
facendo attenzione che, nel caso del prisma, poniamo
la 'punta' nell'origine, in modo dale da avere
parallelepipedi infinitesimi che crescono al crescere di 'x':
→ questo modo di procedere, francamente innaturale ai fini del solo calcolo del volume, ci servirà a capire meglio i dati degli affondamenti.
- Overview dei risultati sperimentali ottenuti negli esperimenti
degli affondamento di vari solidi:
- script R: affondamenti_overview.R
(da usare come pseudocodice per scrivere uno script equivalente nel linguaggio preferito); - dati sperimentali: misure_affondamenti.dat;
- per eseguire lo script, tanto per vedere (e tentare di riprodurre/migliorare
i risultati) si veda il file dei comandi
eseguiti durante la lezione.
[Per capire cosa fanno le varie funzioni chiamate si cerchi in rete, oppure, dalla console R, si esegua "?nome_funzione", ad es, "?read.table", "?source", etc.]
(e, importante, il comando per uscire da R è "q()") -
Screenshots: plot 1,
plot 2,
plot 3,
plot 4.
Nota: i segmenti fra un punto sperimentale e l'altro servono solo 'a guidare l'occhio' ('to guide the eye') e non hanno alcun significato statistico/inferenziale!
- script R: affondamenti_overview.R
- Si raccomanda inoltre di rivedere i test di autovalutazione anche alla luce delle risposte di ChatGPT:
- Continuazione del problema
della distanza
della Minerva:
- valutare l'angolo sotteso all'occhio dalla larghezza del pollice, con i dati ivi riportati;
- ripetere l'esercizio mantendo la distanza dito-occhio, ma considerando un mignolo largo 1.0 cm invece del pollice.
- Galleria di immagini e link associati
- Lezione 5 (08/03, 2h)
-
- Avviso: domani useremo
anche l'ora 13-14.
- sessione di Python;
- chi può porti il laptop o tablet, o organizzarsi con qualcuno per lavorare indieme;
- si raccomanda di provare già a trascrivere in Python quanto fatto nella scorsa lezione;
- script R (non mostrato a lezione) per continuare l'analisi:
→ provare ad eseguirlo 'as is';
→ 'tradurlo' (con variazioni/migliorie a piacere) in Python.
- Raccomandazioni per la soluzione dei problemi:
- partire da una figura, dalla quale sia chiaro il significato dei simboli;
- risolvere il problema usando i simboli
e non i valori numerici
arrivando così a una formula risolutrice; - sostituire quindi nella formula le varie grandezze di input;
- trattare le unità di misura in modo algebrico,
riscrivendo eventualmente il risultato con una unità di misura
equivalente e adatta al problema:
→ check dimensionale; - eseguire i conti della parte numerica, facendo
attenzione alle cifre significative:
→ check dell'ordine di grandezza del risultato (quando è possibile — sforzarsi!)
- Problema della Minerva,
mediante opportune proporzioni
(soluzione in aula del problema — la base della statua, misurata da alcuni studenti, è pari a 155 cm). - Calcolo del volume della sfera mediante la somma di infiniti dischetti di spessore infinitesimo.
- Possibile approccio alternativo, vedendo la sfera
come composta da infiniti gusci sferici concentrici di spessore
infinitesimi
[dV = S(r) dr; → integrale]- maper eseguire il conto bisogna conoscere la formula
della superficie della sfera di raggio R:
→ ?? (sì, la formula è nota, ma come derivarla da concetti elementari?); - usiamo "dV = S(r) dr" 'al contrario', ovvero
S(r) = dV/dr (derivata nella notazione di Leibnitz): → conto banale
(e finalmente si capisce la relazione fra i coefficienti della formula del volume e quelli della formula della superficie!).
- maper eseguire il conto bisogna conoscere la formula
della superficie della sfera di raggio R:
-
A proposito di gusci sferici, torniamo al problema
della forza peso nell'ipotetico
pozzo per il centro della Terra
(nel quale ChaGPT ha fallito miserabilmente!):
— considerando la Terra come una cipolla, formata di tanti gusci sferici concentrici (e stessa densità superficiale per ciascun guscio)
— e data r la distanza del punto materiale di massa m dal centro della Terra (di raggio RT)- la somma delle forze dovuta a ogni guscio avente
raggio maggiore di r danno risultante nulla
[con il semplice ragionamento mostrato in aula, o vedi qui, anche inutilmente complicata (basta pensare a coni di apertura infinitesima)]; - per quelli aventi un raggio minore o uguale a r
la cosa è più complicata
e bisogna fare un integrale (→ Teorema del guscio sferico). - Quindi il punto matriale in r subisce una forza verso
il centro della Terra
- proporzionale a V(r)∝ r3
- e inversamente proporzionale a r2.
- Ma, siccome |F(r=RT)| = m g, otteniamo 'a vista' |F(r)| = m g · r/RT.
- Infine, considerando r come una coordinata
lungo il pozzo con verso positivo 'verso di noi',
otteniamo
F(r) = - m · (g/RT) · r ,
da cui abbiamo, per l'accelerazione in caduta libera,
a(r) = F(r)/m = - (g/RT) · r .
[Memento: la massa che compare in F(r) 'sarebbe' gravitazionale mentre quella che compare in a(r) = F(r)/m 'sarebbe' inerziale,
ma usiamo la stessa notazione e le possiamo semplificare per quanto già detto precedentemente.]
- la somma delle forze dovuta a ogni guscio avente
raggio maggiore di r danno risultante nulla
- Commenti sulla notazione di Leibnitz delle derivate:
- il rapposto fra gli infinitesimi, in generale, dy/dx rende esplicito il limite Δy/Δx per Δx → 0;
- se si conosce la funzione g(x) con cui la derivata
varia in funzione di x, ovvero data
la generica g(x) = dy/dx,
allora- dy = g(x)·dx
- e la variazione finita Δy
è ottenuta come somma degli infiniti elementi dx
→ integrale;
- le grandezze fisiche hanno delle dimensioni (→ unità di misura;) e la notazione di Leibnitz mostra chiaramente le dimensioni della derivata.
- se nel lasso di tempo Δt il punto materiale si sposta di Δx, la velocità media in tale intervallo temporale (e spaziale) sarà pari vm = Δx/Δt;
- la velocità istantanea a un dato istante (e quindi a una data posizione) sarà quindi data da v(t) = dx/dt;
- ne segue che dx = v(t) · dt, etc. etc.
- Dalla Minerva al Cupolone
- uso del diametro angolare dei corpi celesti (tondi) e, in generale, delle dimensioni angolari;
- note sulla trigonometria a partire dai
rapporti dei lati di un triangolo rettangolo (per cominciare)
a parole,- seno: 'cateto opposto diviso ipotenusa';
- coseno: 'lato adiacente diviso ipotenusa';
- tangente: 'cateto opposto diviso cateto adiacente'.
- Prima di risolvere il problema del Cupolone, si affronti
quello della Minerva in due passi:
- valutare la larghezza angolare del dito visto dall'occhio;
- usare questa informazione per valutare nuovamente la distanza occhio-Minerva.
- Altri problemi analoghi: → vedi Galleria
- Avviso: domani useremo
anche l'ora 13-14.
- Lezione 6 (09/03, 3h)
-
- Ancora sulla forza peso nell'ipotetico pozzo
per il centro della Terra,
- con precisazioni varie,
- ma in effetti non si è fatto altro che
ripetere quanto detto nella lezione precedente
(ma se anche ChatCTP ha toppato ci deve essere una ragione...)
- Dalla velocità media alla velocità istantanea (e locale!) — 1D;
Dall'accelerazione media all'accelerazione istantanea (e locale!) — 1D;
→ lavagna. Da cui seguono- Dalla velocità istantanea alla variazione infinitesima di posizione;
- Dall'accelerazione istantanea alla variazione infinitesima di velocità.
sommando le infinite variazioni infinitesime:
→ integrali quando la matematica è 'semplice';
→ metodi numerici quando 'il gioco si fa duro'. - Osservazioni sul fatto che l'acceleratore dell'auto
non sia in realtà un acceleratore, bensì
un 'dosatore di forza'
→ dobbiamo mantenere premuto l'acceleratore (in pianura) anche per procedere a velocità costate;
→ forza dovuta al motore è equilbrata dalle forze di attrito (soprattutto dell'aria). - Sul significato di dv = a(t,x) · dt :
- se a(x,t) è positiva la velocità aumenta;
- se a(x,t) è negativa la velocità diminuisce;
- Sul significato che in prossimità della superficie terrestre
(in assenza di altre)
l'accelerazione sia costante (-g) e indipendente dalla massa del corpo:
problema dell'oggetto (il nostro sasso(*)) lanciato verso l'alto:
quanto vale l'accelerazione del sasso- quando sta viaggiando verso l'alto;
- quando è nel punto più alto e quindi per un istante sta fermo prima di tornare indietro;
- quando sta scendendo?
↠ Variazione nel tempo della velocità (→ derivata → accelerazione) costante e negativa
(*) A proposito: era rimasta in sospesa la domanda su come si poteva misurarne meglio il volume:
→ spinta di Archimede + azione-reazione!
→ bilancia.
- Oggetto sul tavolo:
- analisi delle forze in gioco;
- determinazione delle forze uguali e contrarie secondo il terzo principio.
perché è il gessetto a cadere verso la Terra e non la Terra a sollevarsi verso il gessetto?
↠ è una questione di differenza di inerzia! - Oggetto sul tavolo, fermo, ma anche tirato orizzontalmente mediante elastico:
→ 'cherchez les forces!'- forze sull'oggetto (quattro!);
- forze uguali uguali e contrarie secondo il Terzo Principio.
- forza di attrito statico.
- Di nuovo oggetto fermo (polistirolo, per ricordarci della spinta di Archimede):
→ 'cherchez les forces!'
→ in particolare non è banale la forza uguale e contraria a tale spinta verso l'alto!- blocco di polistirolo su quattro spilli;
- quando avevamo la spinta di Archimede su corpi immersi in acqua
la reazione la 'vedevamo'
→ aumento di lettora sulla bilancia; - nel caso di spinta dell'aria, la reazione si 'scarica' sul 'contenitore dell'aria', ovvero sulla Terra.
→ Solo se si toglie (quasi) completamente l'aria da sotto le cose cambiano: → ventosa!
→ (È ben nota la spettacolare esibizione degli emisferi di Magdeburgo.) - Esperimento qualitativo del blocco di polistirolo sul 'tavolo inclinato':
- fino a un certo angolo di inclinazione il polistirolo rimane fermo (→ attrito statico);
- poi comincia a scivolare (ma con attrito dinamico)
(sul tipo di moto torneremo nel seguito).
- Analisi affondamenti
- Tradurre lo script in Python!
- Problema (importante perché dà un senso ai vari integrali fatti!):
- Dalla geometria degli oggetti affondati ricavarsi i coefficienti attesi ('slope' in figura ) e confrontarli con quanto ottenuta dalla (benché rozza) analisi dati.
Vettori in R → Python:
(L'argomento andrà ripreso da capo)
Nota: è disponibile una dispensa la quale 'crescerà' con il procedere del corso:- Appunti di Fisica (Dispensa 1)
→ Per il suo utilizzo si faccia uso delle note in essa contenute
e/o che saranno date a lezione e/o riportate di volta
in volta in questa pagina.
→ In prima pagina è riportata bene in evidenza la data del suo ultimo aggiornamento,
- Ancora sulla forza peso nell'ipotetico pozzo
per il centro della Terra,
- Lezione 7 (13/03, 2h)
-
- Calcolati i coefficienti ('slope') degli andamenti
lineari (o linearizzati!) degli affondamenti?
- È importante provarci e scambiarsi i risultati
(non verranno esattamente gli stessi numeri riportati sul plot, ma qualcosa di ragionevolmente simile).
- È importante provarci e scambiarsi i risultati
- Problemi ... su altri problemi?
- Volume uovo ('grande', per cui non lo possiamo immergere)?
- Simmetria di rotazione
- Valutazione del 'profilo' (→ r(x)) mediante foto.
- Nota sugli integrali, specialmente in Fisica:
- imparare a scrivere prima
(usando le generiche variabili x e y)
dy = f(x) dx e quindi
→ Δy = 'somma degli infiniti dy'
(Pensare a come era stato introdutto il problema e, quindi, al significato che avrebbe avuto ΔV.)
- imparare a scrivere prima
(usando le generiche variabili x e y)
dy = f(x) dx e quindi
- Delucidazioni sulle note postate online.
- Inventario delle forze incontrate finora:
- Forza di gravità
- inizialmente ipotizzata fra due 'punti materiali';
- estesa quindi a punto-sfera e sfera-sfera;
- caso particolare di oggetto 'in prossimità' della superficie del pianeta Terra;
- estensione all'interno della Terra.
- Campo gravitazionale dal centro della Terra
all'infinito:
→ Galleria
Campo gravitazione all'altezza dell'ISS, valutato a partire da quello sulla superficie terrestre.- espansioni notevoli (tanto più ε ≪ 1, tanto più
sono 'valide'):
- (1±ε)2 ≈ 1 ± 2 ε
- √(1±ε) ≈ 1 ± ε/2
- 1 / (1±ε) ≈ 1 ∓ ε
- 1.082; 0.962; 1.0022; 0.9982;
- √(1.04); √(0.91); √(1.0016); √(0.9984);
- 1/0.98; 1/1.03; 1/0.995; 1/1.005.
Torneremo sull'importanza delle approssimazioni. - espansioni notevoli (tanto più ε ≪ 1, tanto più
sono 'valide'):
- Forza elettrostatica fra due cariche elettriche.
È importante introdurla insieme alla forza di gravità in quanto:
- mette in risalto il significato di 'm' nell'espressione dela forza di gravita;
- fa capire meglio il significato di campo
(concetto usualmente usato solo per il caso elettrico).
→ Doppio significato di g
- Reazione vincolare.
- Forze di attrito
- statico;
- dinamico.
- Spinta di Archimede
- Forza elastica
- Forza di gravità
- Le forze sono grandezze vettoriali
- la sola intensità non basta a definirla in modo univoco;
- servono anche direzione e verso.
La massa invece è una grandezza scalare. - Equilibrio di più forze su due assi (verticale e orizzontale)
su un corpo fermo:
→ caso particolare di a = F / m, con a=0
→ (in questo caso ax = 0 e ay = 0 ).
↠ Problema: trovare la condizione di galleggiamento:- calcolare la frazione di corpo immerso affinché l'oggetto sia in equilibrio
(per semplicità, cominciare ragionando su corpo di densità ρ immerso in acqua); - cominciare a riflettere, qualitativamente, sui problemi di stabilità
(perché una tavola a galla orizzontalmente e non verticalmente, visto che la spinta di Archimede dipende solo dal volume immerso?)
→ la forza peso è vista applicata nel centro di massa del corpo
→ (ovviamente è pari alla somma delle forze agenti su ogni suo 'punto' → vedremo nel seguito il concetto di centro di massa).
→ la spinta di Archimede è vista applicata nel centro di massa del fluido spostato
→ ergo...
- calcolare la frazione di corpo immerso affinché l'oggetto sia in equilibrio
- Introduzione all'Idrostatica
Pressione:- Richiami (dovrebbe essere una grandezza abbastanza nota, vista la sua importanza pratica).
- Unità di misura e 'percezioni' (il pascal è impercepibile!).
Alcuni esempi (per avere l'ordine di grandezza):- pezzettino di foglio da stampanti (cercarsi su internet la 'grammatura');
- moneta da un centesimo (m = 2.35 g; d = 1.63 cm);
- moneta da un euro (m = 7.46 g, d = 2.33 cm);
- altri oggetti a piacere...
- Precisazioni
- grandezza scalare o vettoriale?
- pressione all'interno dei fluidi: → Galleria
- Quindi,
nella lista delle forze possiamo aggiungere
la forza di pressione all'interno di un fluido:
- proporzionale alla pressione;
- normale (ovvero trasversale) alla superficie (anche 'infinitesima') su cui agisce;
- proporzionale all'area (anche 'infinitesima') su cui agisce.
- Altra forza di importanza pratica (a cui abbiamo inevitabilmente fatto cenno):
↠ resistenza dell'aria.
Peculiarità- solo se l'oggetto è in moto (e questo è vero anche per l'attrito dinamico);
- dipendenza dalla velocità: più aumenta la velocità e più aumenta la resistenza:
- per l'aria dipendenza quadratica (ma la cosa può essere più complicata);
- per altri fluidi ('viscosi') dipendenza lineare
(usata anche come semplice modello didattico).
→ fisica del paracadutista
↠ Quindi il numero di forze incontrate finora è pari a otto (o nove se vogliamo considerare attrito statico e dinamico come forze diverse).
- Moti 'visti' (o immaginati, o lasciati all'esperienza) finora:
- moto a velocità costante;
- moto uniformemente accelerato (corpo lasciato cadere);
- moto uniformemente decelerato (corpo lanciato in aria verticalmente)
- moto che tende a velocità costante (palloncino lasciato cadere).
- Altri problemi:
- trovare il campo gravitazionale. gL,
dovuto alla Terra alla distanza a cui si trova la Luna,
il quale, come sappiamo ci dà anche il valore dell'accelerazione
in caduta libera.
(In questa caso basta ricordarsi che la forza di gravità va come 1/d2, e per d possiamo prendere 400 mila km.) - Una volta trovati i valori di g, gISS
e gL, espressi in m/s2,
calcolare lo spazio di caduta
libera nel primo secondo per un corpo inizialmente a riposo
- in prossimità della superficie terrestre;
- alla quota della stazione obitale ISS;
- alla distanza a cui si trova la Luna.
- chi ha fatto queste cose alle superiori usi la formuletta che conosce;
- chi non conosce tale formuletta si arrangi (per il momento), anche chiedendo eventualmente a ChatGPT.
- trovare il campo gravitazionale. gL,
dovuto alla Terra alla distanza a cui si trova la Luna,
il quale, come sappiamo ci dà anche il valore dell'accelerazione
in caduta libera.
Variante dello script R per analizzare gli affondamenti, il quale non fa uso di lm(): → dovrebbe essere più facile 'tradurla' in Python - Calcolati i coefficienti ('slope') degli andamenti
lineari (o linearizzati!) degli affondamenti?
- Lezione 8 (15/03, 2h)
-
- Altri 'oggetti' idealizzati nei problemi di meccanica:
- funi inestensibili e senza peso
- tensione (la forza con cui tira o viene tirata)
→ altra forza (nona-decima) da aggiungere all'inventario; → come per la reazione vincolare e per l'attrito statico, il valore della tensione è ricavato dal 'contesto' (ma in questo caso l'oggetto può essere anche in movimento).
- tensione (la forza con cui tira o viene tirata)
- carrucole senza massa ('senza inerzia'!) e senza attriti
→ servono solo a cambiare direzione e verso della tensione delle funi.
- funi inestensibili e senza peso
- Nuovo script per l'analisi degli affondamenti:
analisi_affondamenti_1.R
→ tradurre in Python! - Metodo con cui vengono calcolate del slope
nel nuovo script [→ function slope()], illustrato
un po' alla buona.(*)
- Si cerca la retta 'y = m x' passante per l'origine (ok per gli affondamenti) e 'al meglio' fra i punti sperimentali, con generiche x e y fra cui si assume un andamento lineare.
- Si potrebbe cercare m che minimizza la somma delle distanze
fra i punti sperimentali e la retta,
MA- la formula della distanza 'non è simpatica'...
- e, soprattutto, tale distanza non ha senso (una mostruosità!) in quanto in Fisica (e in generale) x e y hanno dimensioni fisiche.
- Si può pensare quindi di minimizzare la somma
delle distanze fra yi misurato per
un certo xi e in valore dato dalla retta
per quell' xi,
ovvero di = | yi - m· xi|; - In realtà, essendo la funzione modulo 'scomoda', si preferisce
minimizzare la somma dei quadrati degli scarti lungo y:
→ S(m) = Σi di2 = Σi (yi - m· xi)2,
ove è stato scritto esplicitamnte che S è funzione di m. - Si può ricavare, con un paio si passaggi, che il valore
di m che minimizza S(m) è dato
dal rapporto fra la media dei prodotti x·y
la media dei quadrati di x.
Nota Una ben nota difficoltà è che nei corsi di matematica le 'funzioni' sono 'funzioni di x', le derivate si fanno rispetto a x, etc. etc..
È importante quindi cominciare a imparare che- in Fisica e in tutte le Scienze, una grandezza di interesse può essere funzione di una o più grandezze aventi in genere anche delle unità di misura.
- in genere può avere interesse di capire come varia la funzione rispetto
a una sola delle altre,
lasciando le rimanenti invariate, da cui il concetto di derivata parziale (la voce italiana è pessima...).
- derivative of 5 x^2
- derivative of m x^2 [da notare come nella risposta è cambiato il simbolo di derivata!]
- derivative of m x^2 wrt m
- derivative of m x^2 y^3 wrt y
- derivative of A cos(omega t + phi)
→ Wolfram Alpha è in grado di capire che in una funzione del genere la variabile 'di interesse' (di default) è t
anche se gli si può indicare esplicitamente rispetto a cosa derivare, ad es:
- Ancora forze di pressione:
- equilibrio di fluidi stazionari ('a riposo'):
→ la pressione può solo dipendere dal 'livello' (o profondità); - vasi comunicanti;
- legge di Stevino e paradosso idrostatico (ne riparleremo a lezione);
- legge di Archimede riottenuta dalla legge di Stevino:
→ lasciata come esercizio.
- calcolare dP/dh per acqua e aria (il primo caso è già stato visto a lezione);
- continuazione del secondo caso, con riferimento al blocco
di polistirolo (→ prima lezione):
- si calcoli la variazione di pressione fra superficie superiore e superiore nei casi in cui il blocco sia verticale e orizzontale;
- si calcoli le forze di pressione sopra e sotto nei due casi;
- si calcolino, dalle forze di prossione sopra e sotto, la spinta di di Archimede nei due casi.
- La 'ventosa'
mostrata a lezione
era costituita da due ventose, ciascuna di diametro 11.7 cm.
Calcolare la forza necessaria per staccarla, dopo che ha perfettamente aderito a un piano liscio, esprimendone il valore sia in newton che in chilogrammo peso (o chilogrammo forza).
- equilibrio di fluidi stazionari ('a riposo'):
- Vettori in Fisica, per ora limitatamente
a forze, acceleraioni e velocità
[+ spostamenti e 'vettori posizione' ('raggi vettori') ] - Problemi tipici (nelle righe che seguitano il grassetto indica
una grandezza vettoriale):
- s(t) → v(t) → a(t)
[ → F(t)]
Nota se è nota la funzione s(t), possiamo (almeno in principio) invertirla e quindi ricavarci v(s), a(s), etc. - F(s,t) → ... → ... → ...
- s(t) → v(t) → a(t)
[ → F(t)]
- Alcuni esempi classici:
- moto uniformemente accelerato
(→ spazio percorso nel primo secondo in alcuni casi notevoli); - lancio di oggetti (soggetti alla sola forza peso);
- Un oggetto è lasciato cadere da 3 m di altezza.
Calcolare (trascurando la resistenza dell'aria, assunzione valida anche per i problemi che seguono)- il tempo impiegato a raggiungere il suolo;
- la velocità raggiunta 'un istante' prima dell'impatto.
- Un oggetto è lanciato verso l'alto e arriva a 2 m di altezza dal punto
in cui si è staccato dalla mano. Calcolare:
- la velocità con la quale si è staccato dalla mano:
- il tempo impiegato a raggiungere il punto più alto.
- Un oggetto è lanciato, inizialmente su un punto di un piano
orizzontale è lanciato con un certo angolo, rispetto al piano
orizzontale,
tale che vx = vy = 10 m/s.
Calcolare- il tempo impiegato a raggiungere il punto più alto;
- la quota raggiunta;
- il tempo necessario per ritornare alla quota iniziale;
- il tempo di volo, ovvero l'intervallo temporale da quando è stato lanciato a quando è tornato alla quota iniziale;
- lo spazio percorso orizzontalmente in tale lasso di tempo.
- moto uniformemente accelerato
- Altri 'oggetti' idealizzati nei problemi di meccanica:
- Lezione 9 (16/03, 2h)
-
- Tornando all'espressione per valutare la slope 'm'
della retta che passa 'fra i punti sperimentali' e per l'origine:
- era veramente necessario dividere le sommatorie per n?
→ Vantaggio di dare alle formule un significato facilmente memorizzabile. - E, a proposito, torniamo al vecchio problema della velocità
media, viaggiando nella prima metà di un percorso
a velocità v1 e nella seconda metà a
velocità v1.
→ Media 'famose' (per chi ne aveva già sentito parlare... altrimenti fuori programma per il momento)- media aritmetica;
- media geometrica;
- media armonica.
→ media pesata (concetto applicabile a ciascuna delle tre medie listate sopra — non è un'altro tipo di media).
- era veramente necessario dividere le sommatorie per n?
- Spazio di caduta nel primo secondo nei tre casi proposti:
→ risultati numerici?
→ è importante avere in mente i diversi ordini di grandezza.
→ serve a far capire come istante per istante anche la Luna cade verso la Terra → cannone di Newton - Problema del sub 'in apnea' (su domanda di uno studente):
- 'sembra' che dopo 10-15 m di profondità venga meno la spinta di Archimede;
- ?? → Gli interessati possono investigare (eventualmente anche ponendo la domanda a ChatGPT);
- intuitivamente vien da pensare che sia dovuto al fatto che (fortunatamente) non siamo dei solidi: → la pressione tende a ridurre un po' il volume, mentre la massa resta invariata.
- Dal moto uniformemente accelerato unidimensionale
al caso 2D (e l'estensione al caso 3D va da sé).
Ricordiamo la regola generale (almeno per questo tipo di problemi):
- 'ogni coordinata va per conto suo, mentre il tempo è comune'.
- corpo lasciato cadere o lanciato verso l'alto (→ lezione scorsa);
- corpo lanciato con componete orizzontale
della velocità diversa da zero:
- problemi di lanci di vario tipo;
- lanci nei quali è dato il modulo della velocità iniziale e l'angolo rispetto al piano orizzontale.
- problemi di 'gittate' (ci ritorneremo)
- Introduzione al moto circolare (uniforme, per cominciare)
- Per una rappresentazione grafica animata del
moto circolare uniforme
→vedi Galleria - Possibili variabili per descrivere il moto circolare: g(t), s(t), θ(t).
→ uniforme significa che essere crescono linearmente con il tempo
→ → vedi Galleria - relazioni fra periodo T e le varie 'velocità';
- Analisi del moto circolare uniforme mediante le coordinate cartesiane
(grassetto per indicare vettori):
r(t) → v(t) → a(t),
ove r(t) = ( x(t), y(t) ) = ( R·cos(θ(t)), R·sin(θ(t)) ), con θ(t) = ω t.
[ → v(t) e a(t) seguono derivando rispetto a t ] - Si noti, in particolare, l'importante relazione
a(t) = - ω2·r(t) ,
da cui a = ω2 R,
mentre dall'espressione del vettore v(t) si ricava v = ω R. - Importanti osservazioni di carattere dimensionale:
- θ, sebbene abbia una unità di misura ('un nome', il radiante), è adimensionale in quanto — si ricorda — il radiante è definito come rapporto fra grandezze omogenee ('arco diviso raggio');
- la velocità angolare ω ha quindi la dimensione dell'inverso di un tempo (→ dθ/dt), ovvero s-1 nel S.I.;
- in particolare, si noti come gli argomenti delle funzioni
trigonometriche sin(), cos() e tan()
debbano essere adimensionali.
→ Controllo dimensionale! - Anche altre importanti funzioni, come l'esponenziale
e il logaritmo
devono avere argomenti adimensionali!
→ Controllo dimensionale!
- Rappresentazione grafica di velocità
e accelerazione nel moto circolare uniforme
→ vedi Galleria
→ eseguire/modificare lo script R con cui è stata prodotta la figura e 'tradurlo' in Python. - Accelerazione centripeta e forza centripeta:
Nota: la forza centripeta non è un altro tipo di forza, da aggiungere alla nostra lista, bensì il nome che si dà a una forza che constringe un corpo a muoversi su una traiettoria circolare. Quindi, a seconda dei casi essa può esser dovuta, ad esempio, a- forza gravitazionale (satelliti in orbita, etc.);
- tensione di una 'corda' (fionda di Davide o lancio 'martello');
- attrito statico (auto che curva);
- forza di Lorentz (particella carica soggetta a solo campo magnetico);
- ...
- Esercizio farsi delle tabelle fra le varie grandezze che si incontrano
nel moto circolare uniforme (R, T, ν, ω, v, a) senza tentare di ricordarle a memoria
→ quali sono quelle importanti da ricordare?
- Problema: dopo il caso uniforme, il caso immediatamente più
interessante è quello in cui la velocità angolare varia linearmente
con il tempo, ovvero dω/dt = α (con α costante e avente il significato
di accelerazione angolare)
- in analogia al 'normale' moto uniformemente accelerato, ricavarsi
l'espressione di
- ω(t)
- e di θ(t)
- dopo aver inserito quindi θ(t) [al posto di 'ωt']
nelle espressioni di x(t) e y(t), dipendenti
dalle funzioni cos() e sin(), ricavarsi
- v(t), ovvero vx(t) e vy(t);
- a(t), ovvero ax(t) e ay(t);
- (per i più esperti) ripetere in questo caso quanto fatto per ottenere
la rappresentazione grafica dei vettori velocità e accelerazione in funzione del tempo
(analogo a quanto mostrato in Galleria per il moto circolare uniforme)
- in analogia al 'normale' moto uniformemente accelerato, ricavarsi
l'espressione di
- Per una rappresentazione grafica animata del
moto circolare uniforme
- Lista di comandi usati nella sessione
R mostrata a lezione (tutti, anche con eventuali errori!):
→ riordinare, organizzare in script, effettuare modifiche
a piacere, etc. etc.
[Nota: a causa del noise randomico aggiunto alla y mediante rnorm(), eseguendo più volte y <- m0 * x + rnorm(10, 0, 0.5) non si otterranno mai esattamente gli stessi valori di y.]
- Tornando all'espressione per valutare la slope 'm'
della retta che passa 'fra i punti sperimentali' e per l'origine:
- Lezione 10 (20/03, 2h)
-
- Paradosso idrostatico
e, a proposito,- dispensa_pressione.pdf
→ fino al par. 2.13.1 (ovvero fino a p. 106 della dispensa, ovvero p. 9 del file pdf — poi la riprenderemo).
- dispensa_pressione.pdf
- Moto circolare prima uniforme e poi, dopo un giro accelerato:
- vedi problema suggerito la lezione scorsa;
- soluzione mediante grafica 'animata' eseguendo lo script
(→ da 'tradurre' in Python)
→ vedi Galleria
- Retta per due punti (argomento ben noto?)
- Prodotto scalare:
- 'vecchia dispensa', par. 10.4 (pp 50.51) fino alla Eq. (201).
- Esempio di prodotto scalare in R (→ da tradurre in Python): (la cosa forse 'più complicata' è la funzione print.vec() per stampare un vettore, ma si può fare come si crede).
- Altro esempio, in 2D, con grafica (→ Galleria):
- Uso del prodotto scalare,
per questa parte di programma, con alcuni problemi:
- mostrare che nel moto circolare uniforme
- il vettore v(t) è sempre normale al vettore r(t);
- il vettore v(t) è sempre normale al vettore a(t);
- il vettore a(t) è sempre opposto al vettore r(t).
- mostrare che la 1.1 è valida anche per
un moto circolare uniformemente accelerato
(→ problema proposto in fondo all'ultima lezione)
- mostrare che nel moto circolare uniforme
- A proposito della 'vecchia dispensa'
(per il momento)
- par. 2.1-2.4, pp. 3-5 (moto rettilineo con velocità uniforme o accelerazione variabili)
- par. 5.2-5.4, pp. 10-12 (moto circolare uniforme)
- par. 5.5, p. 13 (seconda legge di Newton)
- par. 6.2, p. 14 (dimensioni e unità di misura)
- par. 6.3-6.6, pp. 16-20 (esempi di forze e azione-reazione)
[il par. 6.6.1 è assegnato, al momento, come esercizio]
→ dipendenza dalla velocità dello spazio di frenata;
→ equazione oraria (o grafico orario) vs traiettoria (p. 20); - par. 6.7, pp. 20-21 [corpo sospeso a corda: dettagli lasciati come esercizio]
- par. 7.3, pp. 24-25 (pozzo per il centro della Terra);
- par. 7.4, pp. 25-26 (attrito statico e attrito dinamico)
- par. 8.2.1 pp. 30-31 → lezione odierna : → velocità massima in curva;
- par. 8.2.2 pp. 31-32 → lezione odierna: → terza legge di Keplero.
- Moto della stazione orbitale (in approssimazione circolare), assumendo
un'altezza dalla superfice terrestre di 400 km.
Ricavarsi (problemi):- periodo di rotazione;
- velocità (in m/s e in km/h);
- velocità angolare;
- tempo per 'attraversare' (passandogli davanti) un oggetto avente una dimensione
angolare di mezzo grado
(immaginarsi a cosa ci servirà questo tempo!).
( → cannone di Newton )
facendo dipendere le formule, come abbiamo fatto a lezione per il pozzo per il centro della Terra, da g e RT invece che da G e MT.] - Satelliti geostazionari: imponendo T = 24 h, valutare,
risolvendo semplici problemi,
- distanza dal centro della Terra;
- distanza dalla superficie terrestre;
- velocità orbitale.
- E, a proposito di dimensioni angolari e di ISS, ulteriori problemini:
- dimensione angolare della ISS 'circa allo zenith' (assumiamo sia 100 m e altezza 400 km);
- confronto con la dimensione angolare della Luna (anch'essa 'circa allo zenit', per ovvi motivi);
- come cambiano i risultati se la stazione orbitale
è in una posizione intermedia fra orizzonte e zenitn?
(Per semplicità si usi un modello di Terra 'piatta', valida sicuramente 'localmente' — eventualmente da precisare).
- Paradosso idrostatico
- Lezione 11 (22/03, 2h)
-
- Chiarimenti su problemi.
- Note metodologiche sulle trattazioni dei vari moti
di punti materiali incontrati
(vettori in grassetto)
- analisi del moto a partire da s(t):
s(t) → v(t) → a(t) [→ F(t) ]; - moto accelerato ('normale'):
[F(t) →] a(t) → v(t) → s(t); - moto circolare uniforme:
r(t) → v(t) → a(t) [→ F(t) ]; - moto circolare accelerato (con dω/dt = α):
α(t) → ω(t) → θ(t) → r(t) → v(t) → a(t) [→ F(t) ]
ove, nel caso più generale, F(t) può dipendere direttamente anche da s(t) e da v(t) - analisi del moto a partire da s(t):
- Ancora sui corpi orbitanti intorno alla Terra (orbite circolari per semplicità):
- dipendenza del periodo dalla distanza;
- dipendenza della velocità dalla distanza
A proposito: evidenza di Materia oscura nelle galassie (curiosità fuori programma). - velocità e periodo di rotazione
- corpo in ipotetica orbita radente;
- ISS;
- satelliti geostazionari;
- Luna.
- A proposito della Terza Legge di Keplero mostrata nella figura
in Galleria
- Linearizzazioni di andamenti di potenza.
- Uso di scale logaritmiche e di carta logaritmica
Dettagli in Le basi del metodo sperimentale, par. 6.7.4, pp. 105-106, con qualche osservazione- I passaggi importanti sono
- Eq. (6.27), che definisce l'andamento, prontamente linearizzato nella (6.28);
- α rappresenta quindi la pendenza (slope)
dell'andamento linearizzato e
si ricava dal rapporto incrementale della (6.31),
possibilmente riscritto come il rapporto dei log di y2/y1 e di x2/x1
(questa scrittura elimina il problema delle unità di misura,
in quanto gli argomenti dei logaritmi devono essere adimensionali,
di cui si disquisisce a cavallo fra pp. 105 e 106). - Infine, una volta trovato α, si applica
la (6.27) a uno qualsiasi dei punti sulla retta
e,
invertendo la relazione, si arriva alla (6.33) per β [per capirsi, la (6.32) è una inutile complicazione].
- I passaggi importanti sono
- Esempi:
- dati dei pianeti:
- soli dati (in formato per essere usati da R): dati_pianeti.txt
- pianeti_overview.R
- pianeti_log.R
- dati degli affondamenti: analisi_affondamenti_log.R
- dati dei pianeti:
- Per esercitarsi: provare a linearizzare i cinque
andamenti
riportati in dati_potenze.txt- usando la carta logaritmica distribuita a lezione
('preziosa' e quindi riportare i punti con matita leggera); - mediante opportune opzioni dei programmi di grafica del vostro linguaggio preferito.
e confrontarli con quelli riportati in dati_pianeti.txt. - usando la carta logaritmica distribuita a lezione
- Ancora dimensioni angolari e approssimazioni
[ sin(θ) ≈ tan(θ) ≈ θ, per θ << 1; da cui cos(θ) ≈ 1 - θ2/2
→ verificare con calcolatrice/Phyton/... ricordando che θ deve essere in radianti]
Problemi- Vecchio problema della distanza del
Cupolone.
→ Per la dimensione angolare rapportata a quella del Sole ci si arrangi!
→ Importanza di ricordare 1/θ per Sole e Luna (per i dati vedi qui)- 1/θSole ≈ 107 (± 2%) → ≈ 105-109;
- 1/θLuna ≈ 115 (± 6%) → ≈ 110-120.
- si faccia il conto a ritroso, ricavandosi la dimensione angolare dalla larghezza in metri e dalla distanza ottenuta;
- si osservi la foto intera (quella postata sul sito è un ritaglio).
- Dimensione angolare della ISS 'circa allo zenit' (assumiamo sia 100 m e altezza 400 km).
- Confronto con la dimensione angolare della Luna ('circa allo zenit').
- Come cambiano i risultati se la stazione orbitale
è in una posizione intermedia fra orizzonte e zenit?
(Per semplicità si usi un modello di Terra 'piatta', valida sicuramente 'localmente' — eventualmente da precisare).
- Vecchio problema della distanza del
Cupolone.
- Alcuni media spettacolari (fake o veri? — è importante aver chiaro come
risolvere i problemi del punto precedente sulle dimensioni
angolari!):
- ISS con sfondo Luna
- sorgere Luna Barra
- Codice Phyton per gli affondamenti
(grazie a Francesco Safai Tehrani)
→ Provare a casa.
→ Domani alla terza ora vi potete scambiare suggerimenti per farlo funzionare
- Lezione 12 (23/03, 3h)
— Galleria
-
- Note/chiarimenti sui problemi suggeriti
In particolare:- calcolo della dimensione angolare per oggetti piccoli;
- discussione al video e alla foto con Luna
- Tornando alle misure di densità
(avendo sempre bene in mente l'importante concetto di principio di misura)- densità della Terra:
- densità della Luna:
- V? → Aristarco di Samo e successivi
- M?
- densità del Sole:
- V 'facile';
- M 'facile' (avendo 'misurato la massa della Terra',
ovvero avendo determinato G):
↠ (G + dati orbitali dei pianeti) → MSole.
- Idem per Giove e altri pianeti che
hanno satelliti che orbitano intorno ad essi
(altrimenti occorre valutare le perturbazioni sugli altri pianeti — fuori programma)
- Esperimentino in aula con problemi associati:
↠ lancio orizzontale di una moneta dal piano della cattedra:- Dati sperimentali da usare nelle varie elaborazioni:
- altezza del piano della cattedra rispetto
al pavimento: h = 122 cm
(arrotondamento del valore di 121.8 cm riportato sulla lavagna); - distanze nel piano orizzontale(*) raggiunte nei tre lanci: d1 = 46 cm, d2 = 120 cm, d3 = 167 cm.
- altezza del piano della cattedra rispetto
al pavimento: h = 122 cm
- Domande facili (per ciascuno dei tre lanci):
- tempo 'di volo' [ tv ];
- velocità orizzontale iniziale [ v0x ];
- velocità verticale finale [ vy(tv) ];
- modulo della velocità finale [ v(tv) ];
- angolo di impatto con il pavimento;
- la distanza(*)
fra il punto iniziale (in cui
la moneta lascia il piano della scrivania)
e il punto finale della traiettoria (dove impatta con il pavimento)
- Un po' di grafica
- quattro diagrammi orari sullo stesso plot:
- y(t) e x(t)
(uno per ogni v0x )
→ usare puntini invece di linee continue, in modo da mettere in evidenza le diverse velocità.
- y(t) e x(t)
(uno per ogni v0x )
- tre traiettorie, ovvero y(x)
sullo stesso plot:
→ puntini anche in questo caso.
- quattro diagrammi orari sullo stesso plot:
- Domanda un po' più difficile
(ma solo nel senso che si tratta di una novità)
- valutare lo spazio percorso(*)
nei tre diversi 'voli',
ovvero per le traiettorie dei tre lanci
(Suggerimento, con riferimento l'ultimo plot proposto sopra:
si tratta di sommare, per ciascuna traiettoria, le distanze fra ciascum punto e il successivo.)
- valutare lo spazio percorso(*)
nei tre diversi 'voli',
ovvero per le traiettorie dei tre lanci
- Dati sperimentali da usare nelle varie elaborazioni:
Terza ora: per scambiarsi idee su script Python
- Note/chiarimenti sui problemi suggeriti
- Lezione 13 (27/03, 2h)
-
- Precisazioni su dimensione angolare e velocità angolare
(ci servono per capire foto e video della luna: fake o realistici?):- la dimensione angolare non dipende solo dalla dimensione (in metri) dell'oggetto ma anche dall'angolo di vista;
- per parlare di velocità angolare non è necessario
pensare a un moto circolare su un cerchio:
→ esempio in aula.
- Uso di scale logaritmiche:
- esercizio con carta 'doppiolog' → da fare!
- che leggi di potenza avevano i 'dati' forniti?
- ↠ plot degli stessi dati mediante Python, usando scale log-log.
- Codice Phyton per i pianeti del Sistema Solare
(grazie a Francesco Safai Tehrani)
- pianeti_log.py (→ usa scale logaritmiche)
Problemi da risolvere mediante opportuno script che faccia uso dei dati planetari:- Per ciascun pianeta,
nell'approssimazione di orbita circolare:
- convertire la distanza dal Sole in metri;
- convertire il periodo in secondi;
- calcolare la velocità orbitale, esprimendola in km/s;
- calcolare l'accelerazione centripeta.
- Succesivamente, facendo uso di distanza, accelerazione centripeta
e costante di gravità G,
↠ valutare la massa del Sole dai dati di ciascun pianeta.
- Nota storica fuori programma, ma importante
nelle attività scientifiche
(anche se il termine è nato in ambito marinaio): - Ulteriore guida alla 'vecchia dispensa',
- Par. 2.4 → Fig. 2
- Par. 9.3 (cinematica con integrali)
- Par- 5.2 → Fig. 3
↠ Problema: script Python per riprodurre le tre figure. - Par. 5.3 → Eq. (13)
- Par. 6.2
- Par. 6.6.1
- chiarimento su questo tipo di 'trattazione':
→ non è niente di 'nuovo', ma solo un esercizio; - la sola novità è come arrivare
all'espressione dello spazio di frenata, Eq. (32),
facendo uso di un ragionamento dimensionale
→ si arriva alla dipendenza dai parametri, a parte fattori numerici.
- chiarimento su questo tipo di 'trattazione':
- Par. 6.7
- Par. 7.2 → Eq. (49)
- Par. 7.3 → Eq. (57)
- Par. 7.5.1 → carrucola, tensione, attrito, etc.
- Par. 8.3 → piano inclinato
- Par. 8.4 → pendolo 'semplice'
- Precisazioni su dimensione angolare e velocità angolare
- Lezione 14 (29/03, 2h)
-
- Traccie per il quaderno individuale,
finalmente online.
- Precisazioni/delucitazioni
sul moto di oscillazione del pendolo,
con particolare riguardo all'identificazione delle varie grandezze vettoriali in gioco (→ Galleria) - Molla (con dimostrazione in aula):
- allungamento in funzione della massa sospesa;
- condizione di equilibrio;
- oscillazioni intorno alla posizione di equilibrio.
- Analisi empirica basata su Vecchi dati sperimentali (dati_molla_04-05.png)
(con refusi — in particolare x dovrebbe essere ovviamente in cm!)- trovare, mediante l'uso di carta log-log,
le leggi di potenza che intercorrono
- fra x e m, massa sospesa (e quindi fra x e n, numero di dischetti);
- fra T e m, massa sospesa (e quindi fra T e n, numero di dischetti),
- trovare, mediante l'uso di carta log-log,
le leggi di potenza che intercorrono
- Teoria della statica e dinamica della molla:
→ 'vecchia dispensa', Par 7.2, pp. 22-23.
- Riepilogo di importanti 'relazioni' simili
incontrate in diversi problemi:
- pozzo per il centro della Terra;
- pendolo, in approssimazione sin(θ) ≈ θ
- molla.
- soluzione generale dell'importante relazione;
- soluzione particolare, tenendo conto delle condizioni iniziali;
- oscillatore armonico;
- sul doppio significato di ω
- velocità angolare (moto circolare uniforme);
- pulsazione (oscillazione del pendolo e molla),
in particolare:- nella molla non c'è niente che ruota;
- nel caso del pendolo, invece, l'angolo rispetto
alla normale varia con il tempo
e quindi c'è una velocità angolare, dθ/dt, la quale dipende dal tempo e non va confusa con ω!
- Sulle funzioni seno e coseno e sulle loro derivate
- derivate 'da fisico' (da dispensa sui circuiti): parte 1 e parte 2.
- è importante familiarizzarsi sulle proprietà di queste importanti funzioni
(legate non tanto alle 'cose che girano', quanto alle oscillazioni armoniche, di fondamentale importanza!):- script R basato sui comandi eseguiti in aula, da provare a convertire in Python:
- funzioni_sinusoidali.R
- plot risultanti (importante la nota in fondo!)
- script R basato sui comandi eseguiti in aula, da provare a convertire in Python:
- Traccie per il quaderno individuale,
finalmente online.
- Lezione 15 (30/03, 2h)
-
- Precisazioni e chiarimenti
sui
plot delle sinusoidali, ricordando ancora
che
le derivate rispetto al tempo hanno dimensioni diverse dalla funzione che rappresenta la grandezza fisica da derivare,
come evidente dalla notazione di Leibnitz, p. es. dx/dt o dv/dt, etc. - Riepilogo e precisazioni sui problemi che danno
luogo a oscillazioni armoniche:
- equazioni differenziali vs 'equazioni ordinarie';
- schema di soluzione delle equazioni differenziali,
- soluzione generale;
- soluzione particolare, imponendo le condizioni iniziali
dall'equazione differenziale (nella generica variabile x)
d2x/dt2 = - ω2 x
spiega il motivo per cui le funzioni sinusoidale sono usate anche in problemi in cui non ci siano veri angoli 'fisici'
(la trigonometria è nata per risolvere problemi ... trigonometrici). - Precisazione sulla molla posta verticalmente:
→ non confondere la forza di richiamo F(x) = -k x con la forza totale della molla (bisogna aggiungere -m g)
→ vedi dettagli su 'vecchia dispensa', p. 23. - Perché ω2 (e quindi anche T)
del pendolo e del pozzo per il centro
della Terra non dipendono da m,
mentre invece ci dipende ω2 (e quindi anche T) della molla?
- Calcolo dimensionale: importanza concettuale e alcuni esempi
(guidati dal Rasoio di Occam — con qualche rischio...)- spazio di frenata, conoscendo la velocità iniziale v0 e l'accelerazione (negativa) di modulo |a|;
- dipendenza del periodo di oscillazione della molla da k e m;
- dipendenza del periodo di oscillazione del pendolo da l e g.
- problema della gittata, ovvero del calcolo della
distanza a cui arriva un
'proiettere'
sul piano orizzontale, se 'sparato' con una certa velocità di modulo v e un angolo θ rispetto al piano orizzontale;
- Dettagli, per il caso della molla (per la notazione
vedere ad es. 'vecchia dispensa', pp. 14-15.):
- il periodo ha le dimensioni di un tempo:
dim T = T (si usa anche [T] = [T],
ove il 'T' a sinistra sta per periodo e il T a destra sta per la grandezza tempo. - La costante k ha dimensione legate a quelle
delle forza e della lunghezza:
dim k = dim F / dim x ,
ove le dimensioni della forza si ricava dalla seconda legge di Newton: dim F = dim m × dim a, ovvero dim F = M L T -2;
ne segue che dim k = L T-2 (con 'L' che sta per lunghezza, vedi 'vecchia dispensa', pp. 14) - quindi l'equazione dimensionale di interesse
è T = (L T -2)α
(M)β, da cui si ottengono
α e β
e quindi la dipendenza (a parte fattori moltiplicativi) del periodo dalla massa e dalla costante elastica della molla.
invece delle dimensioni, le unità di misura del Sistema Internazionale (SI).- U[F] = N; U[m] = kg; U[T]= s; etc.
- Abbiamo quindi che U[k] = U[F] / U[x] = N / m = kg m/s2 / m = kg s-2.
- L'equazione dimensionale di interesse diventa quindi
U[T] = (U(k))α (U(m))β, ovvero
s = (kg s-2)α kg β .
- il periodo ha le dimensioni di un tempo:
dim T = T (si usa anche [T] = [T],
- Relazione fra
- l'ipotetica orbita radente
- e il pozzo per il centro della Terra,
- E, a proposito, alla luce di quello che abbiamo imparato,
→ rivedersi la simulazione interattiva del cannone di Newton.
- Precisazioni e chiarimenti
sui
plot delle sinusoidali, ricordando ancora
che
- Lezione 16 (3/4, 2h)
-
- Chiarimenti sul Quaderno Individuale:
- I problemi indicati con '[Extra]' non dovrebbero
presentare grandi difficoltà,
(alcuni potrebbero figurare a p. 28 della Settimana Enigmistica...) - Si prega comunque di chiedere chiarimenti a lezione.
- Come esempio si è illustrato quello 'dei treni'
per insistere sulla raccomandazione
di fare un opportuno disegno/grafico prima di cominciare a scrivere formule. - D'ora in poi è importante (almeno tentare di) risolverli tempestivamente-
- I problemi indicati con '[Extra]' non dovrebbero
presentare grandi difficoltà,
- 'Derivata di una funzione composta (funzione di funzione)',
tipicamente scritta come
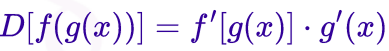
(da math.it)- Chiarimenti sul significato, soprattutto quando la derivata è
fatta,
come spesso succede in Fisica, rispetto al tempo. - Sua riscrittura seguendo la notazione di Leibniz.
- Esempi mostrati (parentesi quadre per enfatizzare su cosa agisce
l'operatore 'd/dt'):
- d/dt [ A sin(θ ] = A cos(θ) · d/dt [ θ ]
(essendo θ funzione di t); - d/dt [ A sin(ω t) ] = A cos(ω t) · ω
- d/dt [ vx2 / 2 ] = vx · d/dt [ vx ] = vx · ax
- d/dt [ A sin(θ ] = A cos(θ) · d/dt [ θ ]
- Chiarimenti sul significato, soprattutto quando la derivata è
fatta,
- Dopo aver visto le consequenze di 'ax · dt'
( → dv ),
concentriamoci su 'ax · dx':- ax · dx = vx · dvx;
- ne segue che l'integrale di 'ax · dx' da x1 a x2 è pari alla variazione di 'vx2/2' da x1 a x2;
- estendendo il ragionamento alle altre due componenti
e riconoscendo nella somma dei prodotti delle componenti di vettori un prodotto scalare
↠ si ottiene una importante relazione (foto lavagna); - infine, moltiplicando entrambi i termini di
tale relazione per la massa m,
si definiscono- lavoro
- e variazione di energia cinetica.
- Quantità di moto e 'riformulazione' (o, più precisamente,
recupero della formulazione originaria)
del secondo principio di Newton (in grassetto i vettori):- p = m v (definizione);
- dp = F dt →
dp/dt = F →
m·dv/dt = F →
dv/dt = F/m (con F
che può dipendere dalla posizione e dal tempo)
[con a sinistra dei simboli '=' l'effetto, a destra la/e causa/e]
- Introduzione alla Termologia.
- Dettagli sulla 'vecchia dispensa':
- Par. 9.5;
- Par. 9.9;
- Par. 10.2, 10.4-10.6;
- Par. 14.6 (fino a p. 72)
Figura in Galleria, con 'dettagli' da chiarire.
- Problemi: → quaderno individuale
- Curiosità fuori programma:
- a proposito di un possibile Python in italiano: Non-English-based programming languages
- ChatGPT Gets Its "Wolfram Superpowers"!
- Chiarimenti sul Quaderno Individuale:
- Lezione 17 (5/4, 2h)
-
- Problemi su lavoro e variazione di energia cinetica:
→ importanti per quello che faremo nelle prossime lezioni! - Valutazione del volume dell'uovo di polistirolo
'affentandolo' a dischetti lungo l'asse principale:
→ Galleria
(il programma potrebbe essere automatizzato trovando il contorno
leggendo le transizioni 'rosso'/'bianco' dei pixel e interpolando opportunamente,
ovviamente assolutamente fuori programma per questo corso, ma compito che l'AI dovrebbe saper fare).
- Ancora Termologia a partire (ancora)
dalla figura in Galleria,
- quantità di calore → caloria;
- capacità termica;
- calore specifico;
- calore latente nei cambiamenti di stato;(*)
- termalizzazione (Principio zero della Termodinamica)
- Dettagli sulla 'vecchia dispensa', Par. 14.6-14.7.; 16.1
che dipende dalle sostanze e dal tipo di cambiamento di stato, la quale indica invece il calore latente specifico
(vedi ad es. Specific latent heat), essendo espressa in cal/g o kJ/kg (da cui si vede chiaramente che è una grandezza specifica).
Si evince quindi che il calore latente — una quantità di calore — è invece pari a Q = λ m.] - Capacità termiche e altre 'capacità' (importanza delle analogie!):
- capacità elettrica
- capacità di storage (HD);
- capacità volumetrica
- quantità di calore(*) ↔ temperatura;
- carica elettrica ↔ tensione;
- quantità di dati immagazzinati ↔ livello di riempimento di un HD;
- quantità di liquido immesso nel recipiente ↔ livello del liquido.
Schema alla lavagna
[(*) seguiranno chiarimenti nelle lezioni successive]
- 'Fisica in cucina' (in realtà solo ABC di termologia):
- l'ebollizione esagerata non serve a niente in quanto la pasta non cuoce prima, visto che l'acqua (fase liquida) non può superare i ≈ 100 °C;
- in realtà non serve nemmeno mantenere
l'acqua intorno a ≈ 100 °C
→ cottura a fuoco spento!
→ per dettagli vedere i video di Dario Bressanini (la cottura non è solo una questione di Fisica, ma più di Chimica);
- Problemi: → quaderno individuale
[sono stati apportati una precisazione e un facile quesito (concettualmente importanti!) al problema nr. 17.1]
Problema supplementare (facile ma importante per capire l'analogia fra le diverse 'capacità'):- Si immagini di avere due recipienti di forma cilindrica posti uno affianco
all'altro.
Il primo, di sezione A1, è riempito di acqua fino al livello h1.
Il secondo, di sezione A2, è riempito di acqua fino al livello h2.
Ad un certo istante i due cilindri sono posti in comunicazione mediante un tubo posto sul fondo.
Per il principio dei vasi comunicanti, dopo un certo tempo l'acqua si stabilizzerà allo stesso livello heq in entrambi i cilindri.
Si calcoli l'espressione di heq.
Ricorda qualcosa?
- Si immagini di avere due recipienti di forma cilindrica posti uno affianco
all'altro.
- Problemi su lavoro e variazione di energia cinetica:
- Lezione 18 (12/4, 2h)
-
- Chiarimenti sui problemi del quaderno individuale
(e teoria sottostante).
- Tubo a U, con dimostrazione in aula
- Richiami di idrostatica.
- Misura della sovrapressione dell'aria all'interno di un palloncino (in eventuali conti, si usi come dislivello fra le colonne d'acqua nei due rami del tubo 30 cm).
- Osservazione delle oscillazioni smorzate.
- Analisi del caso idealizzato, ovvero trascurando gli attriti che portano
a smorzamento:
- indichiamo con x la variazione del livello
dell'acqua dal livello di equilibrio:
- colonnina di destra (come alla lavagna);
- verso positivo di x verso l'alto;
- posizione iniziale con x = xM
e colonna d'acqua a riposo
(analogia con molla e pendolo);
- forza sopra la colonnina a 'sinistra': +Pa·A
(positiva perché spinge la colonninana a sinistra verso il basso, e quindi quella a destra verso l'alto); - forza sopra la colonnina a 'sinistra':
-[Pa·A + ρ·g·(2x)·A]
('2x', indicato con 'h' alla lavagna, perché a un aumento di 'x' a destra corrisponde una diminuzione di 'x' a sinistra); - forza totale: F(x) = - 2ρ·g·A·x;
- essendo la massa dell'acqua nella colonnina
pari a ρ·l·A, con l la lunghezza della colonnina,
e applicando la seconda legge di Newton otteniamo d2x/dt2 = F(x)/m = -(2g/l)·x: ↠ oscillatore armonico con ω2 = (2g/l)
— somiglia curiosamente al pendolo (cosa a cui si sarebbe potuto arrivare mediante analisi dimensionale!).
- indichiamo con x la variazione del livello
dell'acqua dal livello di equilibrio:
- Cenni qualitativi alla fisica dei veicoli:
- importanza dell'attrito statico (*)
- è quello che tiene la macchina in curva;
- è quello che serve ad accelerare e a frenare;
- velocità dei diversi punti di una ruota:
- l'asse viaggia alla velocità dell'auto (essendo solidale);
- in condizioni normali il punto di contatto ha sempre velocità nulla;
- e quindi... che velocità il punto più in alto?
- Siccome (trascurando la resistenza dell'aria)
la forza esterna è data dal terreno e quindi
è applicata ben sotto il baricentro:
- In accelerazione i veicoli tendono a 'impennare':
- Aumenta la forza normale al terreno esercitata
dalle ruote posteriori:
→ aumenta la forza di attrito massima;
→ aumenta la 'presa' con il terreno;
→ trazione posteriore più efficiente. - al contrario, le ruote anteriore tendono a perdere aderenza.
- Aumenta la forza normale al terreno esercitata
dalle ruote posteriori:
- In frenata i veicoli tendono ad abbassarsi davanti:
→ effetto opposto;
→ freni anteriori più efficaci.
- In accelerazione i veicoli tendono a 'impennare':
- Ma la trazione anteriore rende il veicolo più stabile:
→ si pensi a spingere o tirare il carrello della spesa nel caso che le ruote anteriore tendono a impuntarsi.
(Ritorneremo su questi temi quando parleremo dei corpi rigidi).
- importanza dell'attrito statico (*)
- Analogia fra l'espressione della
temperatura di equilibrio di due corpi
(nell'approssimazione di sistema isolato)
e quella del livello di equilibrio fra due serbatoi d'acqua messi in comunicazione (dal basso)
→ problema 18.1 sul quaderno individuale. - Problema su lavoro per riempire un serbatoio d'acqua
→ problema 18.7 sul quaderno individuale.
- Chiarimenti sui problemi del quaderno individuale
(e teoria sottostante).
- Lezione 19 (13/4, 2h)
-
- Chiarimenti su problemi. (Ricordare che
l'impostazione di questo corso è problem solving)
In particolare,- il lavoro compiuto dalla forza peso dipende solo dal dislivello e non dal percorso!
- idem per quanto riguarda la forza di gravità 'in generale',
ovvero dalla superficie della Terra all'infinito
- Consequenze di quanto visto nei problemi con gravità e molla
(trascurando attrito):
- Lavoro totale nullo su un ciclo → forze conservative
- Energia cinetica compare e poi ricompare
→ invenzione dell'energia potenziale - ΔEp|AB = - ΔEc|AB = - L|AB
- Energia cinetica compare e poi ricompare
- Essendo il lavoro pari all'integrale di forza
per spostamento
(caso 1D, con generica variabile spaziale 'x' !!),
→ F(x) = - dEp(x)/dx. - Inoltre siccome
— quello che conta veramente per la dinamica sono le forze
— la forza (conservative!) si riottiene dalla derivata di Ep(x)
↠ ne segue che l'energia potenziale è definita a meno di una costante additiva
↠ (scelta arbitrariamente per semplificare il problema)
↠ in altre parole il punto dove si sceglie Ep(x0) = 0 è arbitrario (bisogna essere solo consistenti con la definizione...) - Casi notevoli:
- forza peso: Ep = m·g·h, con Ep=0 in h=0;
- molla: Ep = ½·k·x2, con Ep=0 in x=0;
- gravità in generale: Ep(R) = -G·M·m/R, con Ep=0 in R→∞ (vedi Galleria)
(per problemi in prossimità della superficie terrestre)
sia un caso particolare del terzo:- si scriva la posizione come 'R = RT + h';
- si espanda R al denominatore di Ep(R), come abbiamo fatto altre volte (ricordando che h ≪ RT);
- risulterà che Ep(R) sarà pari a m·g·h più un termine costante.
- Studio della generica
curva di energia potenziale Ep(x),
funzione della generica variabile x:- essendo F(x) = -dEp(x)/dx, essa è nulla se la derivata
è nulla:
→ punto di equilibrio, il quale può essere- stabile
→ a uno spostamento (dovuto a piccola perturbazione) segue una forza di richiamo;
→ minimo di Ep(x), eventualmente anche locale; - instabile
→ a uno spostamento (dovuto a piccola perturbazione) segue una forza
che tende ad allontanare il punto materiale ancora di più;
→ massimo di Ep(x), eventualmente anche locale. - (Per completezza si aggiunge anche il caso di
equilibrio indifferente,
che corrisponde a Ep(x) 'piatta' in un largo intervallo di x).
in un intorno abbastanza piccolo di un minimo, quadraticamente,
ovvero con f(x) ≈ f(xM) + α·(x-xM)2,
ne segue che in un intorno abbastanza piccolo di un punto di equilibrio stabile
si hanno oscillazioni approssimativamente armoniche.
[Un modo equivalente per arrivare alla stessa conclusione è pensare a una forza
che ha una espressione 'complicata' in funzione della posizione,
ma che può essere riscritta approssimativamente come '-k·x' nell'intorno della posizione di equilibrio
→ per dettagli vedere 'vecchia dispensa', nota 2 a p. 23.] - stabile
- essendo F(x) = -dEp(x)/dx, essa è nulla se la derivata
è nulla:
- Lavoro totale nullo su un ciclo → forze conservative
- Problemi tipici
- molla, caduta gravi, velocità di fuga, etc.
senza usare i tediosi conti della cinematica; - scivoli di varia forma, ricordando che le reazioni vincolari non compiono lavoro
in quanto ortogonali alla direzione di moto (ovviamente stiamo trascurando gli attriti).
→ richiede considerazioni sulla reazione vincolare:
→ → problemi nr. 19.3-19.5 del quaderno individuale.
→ → Galleria
- molla, caduta gravi, velocità di fuga, etc.
- Esperimento fondamentale del Mulinello di Joule:
↠ calore ⟷ energia !- equivalenza cal ⟷ J
- ↠ Energia interna
Può essere aumentata- fornendo calore;
- eseguendo lavoro;
- ...
- ↠ Quaderno Individuale
↠ Chi è in ritardo dia comunque la priorità ai problemi delle ultime lezioni!
(Si ricorda che nel quaderno l'ordine cronologico non è importante,
purché i problemi siano facilmente rintracciabili mediante apposito indice)
- A proposito di antiderivate
- Chiarimenti su problemi. (Ricordare che
l'impostazione di questo corso è problem solving)
- Lezione 20 (17/4, 2h)
-
- Mercoledi 19, lezione ore 11:00-13:00
- Galleria di immagini
- Chiarimenti e approfondimenti su alcuni argomenti visti nelle ultime lezioni.
- Epitaffio di Stevino (di cui non si era ancora parlato a lezione).
- Ancora su lavoro, energia potenziale e energia cinetica,
con ulteriori esempi. - Potenza: energia (scambiata/trasferita/fornita/... )
per unità di tempo:
- W = J / s
- cal/s, kcal/h, ...
- btu/h
- ...
- Ancora calorimetria, con riferimento
alla figura in Galleria:
- precisazioni sul calore latente specifico (λ);
- calore specifico dell'aria: con buona approssimazione 1/4 di quello dell'aria (vedi ad es. qui e qui),
- come mai si riesce a stare abbastanza a lungo in una sauna a temperature prossime a 100 °C.
→ essendo ΔT=1°C assolutamente uguale a ΔT=1K, a meno che non si tratti di note tecnico/scientifiche
→ insistere a scrivere 'K' invece di '°C' nei calori specifici è una inutile pedanteria. - Ancora nota di fisica in cucina: 'cottura in olio' e cosiddetta 'friggitrice ad aria' (definizione non appropriata!).
- Argomenti visti recentemente, (relativamente) nuovi e chiarimenti
sulla 'vecchia dispensa':- par. 9.9;
- par. 10.2-10.7;
- par. 11.1-11.4;
- par. 13-4-13.5;
- par. 14.1;
- par. 14.3-14.7;
- par. 15.1-15.5;
- par. 16.1.
- ↠ Quaderno Individuale
↠ Chi è in ritardo dia comunque la priorità ai problemi delle ultime lezioni!
(Si ricorda che nel quaderno l'ordine cronologico non è importante,
purché i problemi siano facilmente rintracciabili mediante apposito indice) - Mercoledi 19, lezione ore 11:00-13:00
- Lezione 21 (19/4, 2h)
-
- Ancora su questioni energetiche, in particolare sulle
'miracolose' proprietà delle pompe di calore
- Ancora sull'esperimento in aula di lanci di monete
→ calcolo della lunghezza della traiettoria;
→ Nota sul calcolo di integrali: nota_integrale_lanci.pdf
- Un curioso esercizio (per il momento):
data la funzione f(x,t) = A·cos(ω·t - β·x),- si calcolino le derivate seconde sia rispetto a x che rispetto a t,
ovvero d2f/dx2 e d2f/dt2; - si mostri come ω2·d2f/dx2 è uguale a β2·d2f/dt2,
- ... da cui segue, essendo ω2 diverso da zero, che d2f/dx2 è uguale a d2f/dt2 diviso (ω/β)2.
- dire 'che grandezza potrebbe essere' ω/β,
ovvero quali sono le sue dimensioni fisiche.
- si calcolino le derivate seconde sia rispetto a x che rispetto a t,
- Introduzione alla
fotometria
(e radiometria)
→ l'argomento verrà ripreso la prossima lezione.
- ↠ Quaderno Individuale
↠ Chi è in ritardo dia comunque la priorità ai problemi delle ultime lezioni!
(Si ricorda che nel quaderno l'ordine cronologico non è importante,
purché i problemi siano facilmente rintracciabili mediante apposito indice)
- In memoria di Giorgio
Salvini [fuori programma]:
-
Paradosso di Olbers [wiki]
(alla prima lezione del corso di 'Fisica 1' esordì chiedendoci: "Come mai di notte è buio?") - Piccolo contributo a un convegno alla sua memoria
-
Paradosso di Olbers [wiki]
- Ancora su questioni energetiche, in particolare sulle
- Lezione 22 (20/4, 2h)
-
- Oscillazione armonica sul 'fondo' di una
buca di potenziale
- problema nr. 20.5;
- figure in Galleria.
- Ancora sulla funzione
f(x,t) = A·cos(ω·t - β·x),
anche alla luce dei problemi 21.1-21.3:- onde sinusoidali;
- equazione di d'Alambert;
- periodicità temporale: → periodo T = 2π/ω;
- periodicità spaziale: → lunghezza d'onda λ = 2π/β
- velocità di propagazione della 'perturbazione'(!): → velocità v = ω/β = λ/T = λ·ν
→ problema 22.1 del Quaderno individuale.
- Introduzione alla fotometria:
- intro_fotometria_1.pdf
- Si raccomanda di installare una app per misurare
l'illuminamento (lux)
[È importante, come al solito e quando è possibile, familiarizzarsi con gli
ordini di grandezza dei valori numerici delle grandezze fisiche più importanti
→ 'Da sapere', punto nr. 18]
Per avere dei valori di riferimento:
- Complementi:
- Perchè
il cielo è azzurro?
(... e i raggi del sole al tramonto rossi)
(vedi anche qui e in molti altri siti in italiano o in inglese, etc.)
[E "perché le nuvole sotto il cielo azzurro sono 'bianche'?" → pensarci] - "Rosso di sera bel tempo si spera"?
→ Dalle nostre parti è in genere vero- per quanto spiegato nei link qui sopra a proposito dei raggi solari al tramonto
- e perché le perturbazioni arrivano il più delle volte da ovest.
(ma talvolta le perturbazioni possono provenire da est...)
- Perchè
il cielo è azzurro?
(... e i raggi del sole al tramonto rossi)
- ↠ Quaderno Individuale
↠ Chi è in ritardo dia comunque la priorità ai problemi delle ultime lezioni!
(Si ricorda che nel quaderno l'ordine cronologico non è importante,
purché i problemi siano facilmente rintracciabili mediante apposito indice)
- Oscillazione armonica sul 'fondo' di una
buca di potenziale
- Lezione 23 (26/4, 2h)
-
- Commenti su problemi in corso.
- Ancora sulle equazione delle onde,
ripartendo dall'equazione
f(x,t) = A·cos(ω·t - β·x),
che riscriviamo come f(x,t; ω, β) = A·cos(ω·t - β·x) al fine di mettere in evidenza i parametri ω, β da cui essa dipende.- Riscriverla come
- f(x,t; T, λ);
- f(x,t; ω, v)
- Mostrare che una somma di tante onde 'monocromatiche'
Ak·cos[ k·ω0 ·(t - x/v) + φk],
ciascuna avente
- pulsazione (e quindi frequenza) multipla di una pulsazione (e quindi frequenza) fondamentale ω0 (e quindi ν0);
- ampiezze Ak dipendenti da k;
- sfasamenti φk dipendenti da k,
→ Problema 23.1 Quaderno Individuale. - Onde stazionarie come esempio di sovrapposizione di onde:
→ Galleria
- Riscriverla come
- Ancora fotometria (e radiometria)
— intro_fotometria.pdf
(saltando la 'parentesi metrologica' della slide 45)
- Sulla sensibilità logaritmica dei nostri sensi:
- decibel (en passant — vedi decibel in acustica);
- valori luce:
→ vedere EV100 ↔ Illuminance in Table 3 della voce 'Exposure value' (Wiki)
- Inoltre: dalla percezione stereo della nostra vista al
parsec, unità astronomica di distanza di corpi celesti.
- ↠ Quaderno Individuale
↠ Chi è in ritardo dia comunque la priorità ai problemi delle ultime lezioni!
(Si ricorda che nel quaderno l'ordine cronologico non è importante,
purché i problemi siano facilmente rintracciabili mediante apposito indice)
- Commenti su problemi in corso.
- Lezione 24 (27/4, 2h)
-
- Precisazioni sull'angolo solido
- alcune sono analoghe a quelle viste per l'angolo piano,
come il fatto che non è necessario far riferimento ad archi e che dipende dal punto di riferimento; - poi c'è il fatto che non è necessario pensare
calotte o 'dischi' (basi di coni)
[Ad esempio potrebbe aver senso valutare l'angolo solido sotteso dall'Italia rispetto al centro della Terra,
o anche rispetto a un osservato neozelandese o giapponese.]
- alcune sono analoghe a quelle viste per l'angolo piano,
- Ancora fotometria.
- Sovrapposizione di onde:
- interferenza distruttiva
(→ cuffie a riduzione attiva di rumore) - onde 'di fantasia' (+ onda 'quadra' e 'triangolare')
costruite sommando armoniche con opportune ampiezze e fasi (→ Galleria) - Interferometro per la rivelazione di onde gravitazionali
- interferenza distruttiva
- Basi dell'ottica geometrica
- Legge della riflessione e della rifrazione
- Dipendenza dell'indice di rifrazione dalla lunghezza d'onda della luce
- Fenomenologia elementare varia (→ Galleria)
- Materiale vario:
- argomentiFSN_pp35-43.pdf;
- immagini e link in Galleria
(si raccomanda di giocherellare con i simulatori al fine di prender confidenza con la fenomenologia della riflessione e della rifrazione); - vecchia lavagna telematica;
- innalzamento apparente del fondo.
- miraggi
- Cenni (per ora) alla dispersione della luce
(indice di rifrazione dipendente dalla frequenza, ovvero da
λ):
→ vedi figura in Galleria.
- Precisazioni sull'angolo solido
- Lezione 25 (3/5, 2h)
-
- Ottica geometrica
- Regole di base e fenomenologia derivante da essa
- Vecchi lucidi:
- slide1.jpg
- slide2.jpg
- slide3.jpg
- slide4.jpg
→ Galleria, incluso- fronti d'onda piani e sferici;
- difrazione di un'oda elettromagnetica piana nell'attraversare fenditure di diversa larghezza;
- costruzione di sorgenti di onde coerenti;
- esperimento di Young e frange di interferenza;
- simulatore di onda piana che attraversa fenditure;
- analogo dell'esperimento di Young per il caso di eletronni.
- slide5.jpg
- Rifrazione atmosferica
→ Galleria
Altro modo per smascherare media 'costruiti' di Sole e Luna all'orizzonte (ma ci sono anche molte belle foto oneste, ad esempio qui, etc. etc.)
- Ancora sulla fenomelogia legata
alla dispersione dei colori, ovvero a n(λ)
→ Galleria
- Introduzione ai sistemi ottici
Concetto di immagine
- camera oscura (immagine reale)
- specchio piano (immagine virtuale)
- slide7a.jpg
(visione attraverso lastra di vetro versus visione dell'immagine allo specchio)
- slide7a.jpg
Materiale vario:
Problema- Con riferimento alla Fig. 13.5 di MNV(*)
(vedi
Galleria)
e assumendo L = 1 m, d = 10 μm e λ = 600 nm,
- calcolare l'angolo θ a cui si formano la prima, la seconda e la terza frangia luminosa (quella a θ=0 invece è la 'frangia centrale');
- in quali punti x si formano tali frange sullo schermo (la 'frangia centrale' si forma a x=0).
- si ripetano i conti per λ = 400 nm.
- Ottica geometrica
- Lezione 26 (4/5, 2h)
-
- Nota sulla propagazione della luce nei mezzi:
v=c → v=c/n
↠ che succede a λ e ν, rispetto al vuoto? - Nota su fenditure e sorgenti sincrone:
→ figure in Galleria (si veda anche la Figura 13.4) - Dalle due fenditure al reticolo di diffrazione:
— qualitativamente:- l'interferenza dipende dalla lungheza d'onda (vedi problema della lezione scorsa);
- tante fenditure (da cui le onde elettromagnetiche sono irradiate in modo sincrono!) amplificano l'effetto.
→ Il reticolo di diffrazione è una 'alternativa' al prisma per scomporre la luce bianca
→ (molta Chimica e Fisica — etc. etc. — è basata su questa 'scomposizione'!).
- Specchi sferici
- Specchio concavo e analogia con 'antenne sferiche'
e antenne paraboliche (→
Galleria)
↠ Approssimazione per 'raggi parassiali':- asse ottico;
- fuoco (f>0);
- convenzione dei segni;
- raggi notevoli e loro uso per
la costruzione grafica dell'immagine:
→ posizione (q); → grandezza (|y'|); → orientamento (rispetto all'oggetto); - equazione dei punti coniugati (p ←→ q).
- Specchio convesso in approssimazione di raggi parassiali:
analogie e differenze rispetto al caso convesso.
- Specchio concavo e analogia con 'antenne sferiche'
e antenne paraboliche (→
Galleria)
- Materiale vario:
- lavagna_4maggio.jpg
- argomentiFSN_pp35-43.pdf
- Simulazione interattiva su
PhET
- scegliere Mirror (per il momento);
- scegliere Arrow (invece del default Pencil);
- scegliere la curvatura desiderata;
- in Rays scegliere 'Principal';
- giocare con dimensione e posizione dell'oggetto e con le varie opzioni
- Nonostante nella grafica gli specchi mostrino
una curvatura enorme,
con raggi che sembrano ben lontani dall'approssimazione di raggi parassiali 'di Gauss',
i conti sono fatti con tale approssimazione
(altrimenti i diversi raggi riflessi non si incontrerebbero esattamente in uno stesso punto, come mostrato in Galleria)
Si noti comunque come, scegliendo l'opzione Principal Rays viene anche tracciata
una retta verticale tangente allo specchio nel punto in cui esso interseca l'asse ottico:
→ equivalente al disegno schematico dello specchio fatto a lezione. - Con l'opzione
Principal Rays i raggi mostrati sono:
- quello parallelo all'asse ottico e passante per la punta dell'oggetto;
- quello passante per la punta dell'oggetto e diretto verso il fuoco;
- quello passante per la punta dell'oggetto e il punto di intersezione fra specchio e asse ottico.
Il nr. 3 di PhET è ugualmente valido, a parte il fatto che si richiede, nel disegno,
di fare uguali di incidenza e di riflessione uguali
(è più facile tracciare raggi per due punti o paralleli all'asse ottico).
↠ si raccomanda comunque di imparare ad usare i raggi nr. 1 e nr. 2, utilizzabili anche per le lenti.
- Nota sulla propagazione della luce nei mezzi:
- Lezione 27 (8/5, 2h)
-
- Ancora sugli specchi sferici
→ quarto raggio notevole, o principale ('grazie a PhET')
→ Galleria
- Lenti (Galleria
+ argomentiFSN_pp35-43.pdf
(*),
da p. 41)
- Dai prismi alle lenti sferiche (per semplicità solo aria-'vetro'-aria).
- Lenti sottili.
- Formula dei costruttori di lenti.
- Costruzione delle immagini mediante i raggi notevoli.
- Convenzione dei segni (per f, p e q) equazione dei punti coniugati.
(Per quanto riguarda la relazine fra f, p e q in un caso particolare,
ma generalizzabile con un po' di fantasia, si vedano i problemi nr. 27.1 e 27.2)
- Riepilogo e precisazioni su 'vecchi lucidi':
- Ritorno alla meccanica:
- 'vecchia dispensa':
- par. 9.4-9.5 (ripasso di cose note, con osservazioni interessanti)
- par. 9,6: conservazione della quantità di moto (!!)
- par. 9.7-9.8: centro di massa e sua accelerazione dovuta alle sole forze esterne
- Introduzione pratica ai problemi d'urto, :
alla luce della conservazione della quantità di moto.- Urti quasi elastici di un oggetto in movimento contro un oggetto fermo:
- palline circa uguali;
- pallina leggera (ping-pong) contro pallina pesante (da golf);
- pallina pesante contro pallina leggera;
- pallina contro oggetto di massa 'infinita' (pavimento, ovvero edificio, ovvero Terra).
- Urto completamente anelastico contro un oggetto di massa infinita (parete, ovvero...).
- Urti quasi elastici di un oggetto in movimento contro un oggetto fermo:
- 'vecchia dispensa':
- Ancora sugli specchi sferici
- Lezione 28 (10/5, 2h)
-
- Ancora precisazioni sulle unità di misura nel risolvere
i problemi.
Per capire bene la questione, ecco una nota in proposito - Chiarimenti sui problemi in corso
In particolare il nr 27.3, che, per capirne l'intento, è importante avere un'idea delle
dimensioni dei sensori dell fotocamere (→ galleria) - Introduzione al problema nr. 28.1.
- Precisazioni alla luce dell'allungamento
1D del pesce di Tiger
- ingrandimento lineare:
quello che succede alla freccia 'y'
succede a qualsiasi altra freccia ortogonale all'asse ottico
e anche a qualsiasi altra freccia che giace nel piano ortogonale all'asse ottico - diottro sferico (anche se le formule sono fuori programma,
la sostanza è data dalla legge di Snell);
→ goccia d'acqua come lente d'ingrandimento
- diottro cilindrico → bottiglia di Tiger.
- ingrandimento lineare:
quello che succede alla freccia 'y'
- Lente di Fresnel (→ Galleria)
- Urti
'vecchia dispensa':- par. 11.6-11.7;
- par. 11.8, problemi nr. 9, 10, 13, 14 → quaderno individuale
(i restanti sono facoltativi, anche se fortemente raccomandati). - [Par. 13.2 non illustrato a lezione: se ne raccomanda la lettura,
avendo però ben presente che 'la sostanza' è contenuta nei par. 11.6-11.7.]
- Ancora precisazioni sulle unità di misura nel risolvere
i problemi.
- Lezione 29 (11/5, 2h)
-
- Note sui problemi in corso
- 18.3.a: non si poteva rispondere alla domanda;
- 28.4: la risposta al volo dello studente era corretta;
- precisazioni sul problema della lente d'ingrandimento,
- Trasformazione galileiana della velocità
→ 'vecchia dispensa', par. 11.5.
- Andamento temporale del processo di termalizzazione:
- 'vecchia dispensa', par. 16.2
- lavagna_11maggio.jpg
- Nuova (importantissima!) equazione differenziale per la generica x(t):
dx/dt = -α · (x - xF) = -1/τ · (x - xF)
[Nota: Questa scrittura è preferibile alla (385) e simili della vecchia dispensa]
→ andamenti esponentiali
→ τ: costante di tempo
- Alla luce di quanto fatto sulla termalizzazione
si rivedano i problemi 11.4 e 25.6 del quaderno individuale:
→ analogie!
- Introduzione all'inferenza probabilistica
nelle Scienze (e non solo...)
- Slides (prima parte).
- Giochino per enfatizzare l'importanza dello
stato di informazione
nella valutazione di probabilità:
↠ due varianti del problema di tre scatole e un premio:
→ tenere, cambiare o indifferente?
(In genere, coloro che hanno imparato il Monthy Hall senza averlo ben capito
tendono a rispondere erroneamente al primo quesito!)
- Note sui problemi in corso
- Lezione 30 (15/5, 2h)
-
- Problemi in corso, in particolare
- nr. 29.5 e 29.6: P(λi | n,I);
- Andamenti esponenziali
- Un curioso tacchino: → problema nr. 30.5.
- Linearizzazione di esponenziali mediante carte 'semilogaritmiche'
- Dettagli in Le basi del metodo sperimentale, par. 6.7.1-6.7.3, pp. 99-105,
- Dati per esercitarsi all'uso della carta semilog: → problem1 nr. 30.6 e 30.7
- Introduzione all'inferenza (e previsione) probabilistica
nelle scienze.
- Slides: FisiAI_FI2016_02.pdf
- Interessante video di Veritasium
(E anche il libro pubblicizzato alla fine del video è molto interessante!)
- Interessante video su come 'funziona la scienza':
- Storie della Scienza, St. 2021, Ep.8 (soprattutto raccomandati i primi 40')
anche se i dettagli sono fuori programma.)
- Problemi in corso, in particolare
- Lezione 31 (17/5, 2h)
-
- Problemi in corso
- Ancora urti, alla luce di un curioso
video su Youtube
E, a proposito di pi greco e questioni probabilistiche:
- punti sparati in un quadrato che all'interno di un (quarto di) cerchio;
- valutazione di π con un metodo di Monte Carlo;
- inferenza probabilistica di π.
in particolare media e varianza di combinazioni lineari di numeri incerti ('variabili casuali')
- moto con attrito dipendente dalla velocità
con F(v) = -β·v
('fluido viscoso')
→ 'vecchia dispensa', par. 19.5, 19.7.3.
(e 19.8 per altri andamenti esponenziali)
- Inferenza probabilistica (terza puntata):
- Problemi in corso
- Lezione 32 (18/5, 2h)
-
- Problemi in corso, in particolare
→ andamenti esponenziali- figure in Galleria
- par. 19.8 vecchia dispensa
- Ancora su variazione di velocità per effetto di una forza del tipo -βv:
→ dalla soluzione 'canonica' ai due casi di maggio interesse pratico- FM nulla e velocità iniziale non nulla;
- caso opposto.
- Analisi passando per il sistema del centro di massa dell'urto
perfettamente elastico di due punti materiali di massa uguale.
→ 'vecchia dispensa', par. 13.3
- Note sulla gaussiana... e Gauss:
- analisi dimensionall della formula della densità di probabilità;
- sulla derivazione di Gauss della 'gaussiana' (distribuzione
già nota a Laplace e altri francesi):
→ bayesian_reasoning_Gauss_gaussian.pdf,
→ [curiosità storica fuori programma da GdA, "Bayesian reasoning in data analysis"].
→ "The Gauss' Bayes Factor".
- Ritorno a forze gravitazionali e forze elettriche
- Forze e campi (ripasso e precisazioni).
- Energia potenziale e potenziale;
- Un curioso 'circuito gravitazionale' e suo equivalente elettrico.
- Peculiarità del caso elettrico:
- generatori di differenze di potenziali ('tensione');
- trasporto delle differenze di potenziale mediante conduttori (caso statico);
- misurare di differenze di potenziale;
- scorrimento di cariche elettriche e misure di corrente elettrica;
- legge di Ohm.
- forze_gravitazionali_e_elettriche.pdf (fino a par. 1.4 incluso).
- Problemi in corso, in particolare
- Lezione 33 (22/5, 2h)
-
- Problemi in corso, in particolare
- uso dei fattori di Bayes
(e, a proposito, ovviamente fuori programma, libro sul tema); - nr. 31.5 estendere a 99 possibilità per p, 0.01 a 0.99;
- 'passeggiata in Galleria', con commenti e precisazioni.
- uso dei fattori di Bayes
- Calendario esami
e consegna quaderno.
- Circuiti in corrente continua
(v.d. par. 17.5-17.7, 17.9-17.11, 18.2, 18.6, 18.9-18.10)
Modellizzazione (a partire dall'analogia gravitazionale)- generatore: mantiene ai suoi capi la ddp f
indipendementente da dove è posto, la corrente che lo attraversa, etc.; - fili di collegamento: superfici equipotenziali;
- `resistori' (e quant'altro è attraversato da corrente):
- 'obbediscono' alla legge di Ohm;
- dissipano potenza per effetto Joule
- combinazione di resistori:
- in serie sono attraversati dalla stessa corrente
→ resistenza della serie pari alla soma di Ri; → la tensione ai capi della serie è ripartita
→ fra in vari resistori proporzionalmente al valore di ciascuna resistenza
→ partitori di tensione; - in parallelo hanno ai capi la stessa ddp
→ reciproco di Rp pari alla somma di 1/Ri; → la corrente ai capi del parallelo è ripartito
→ fra in vari resistori proporzionalmente a 1/Ri di ciascuna resistenza
→ partitori di corrente.
- in serie sono attraversati dalla stessa corrente
- Leggi di Kirchhoff, basate su
- campo elettrico conservativo;
- conservazione della carica elettrica.
→ esempio: circ_fig_2_16.png- f1 = 2.1 V, f2 = 1.9 V;
- R1 = 45 Ω, R2 = 10 Ω, R3 = 10 Ω.
- generatore: mantiene ai suoi capi la ddp f
- Storielle sui cavi per far partire un'automobile
con la batteria scarica:
→ quando le correnti in gioco sono elevate,
le cadute di tensione sui cavi possono essere non trascurabili:
→ la differenza di potenziale ai capi dell'utilizzatore può differire significativamente
→ rispetto a quella del generatore!
Nota: è stata aggiunta una domanda (intermedia) al problema nr 33.2.

- Problemi in corso, in particolare
- Lezione 34 (24/5, 2h)
-
- Problemi in corso
- Indicazioni sul problema 34.3
- Oscillatore smorzato: introduzione:
- sappiamo come si evolve nel tempo la generica variabile x
se è legata alla sua derivata seconda dall'equazione differenziale
d2x/dt2 = - ω2·x
- sappiamo
come si evolve nel tempo la generica variabile x
se è legata alla sua derivata seconda dall'equazione differenziale
dx/dt = α·x
che, nel caso x sia una velocità (v ), diventa
dv/dt = α·v ,
nel caso di interesse
dv/dt = -(β/m)·v ,
ovvero
d2x/dt2 = -(β/m)·dx/dt ,
- Caso di moto con forza elastica e `attrito di viscosità
-β·v, ovvero
-β·dx/dt :
↠ m·d2x/dt2 = - k·x - β·dx/dt
↠ d2x/dt2 + (β/m)·dx/dt + (k/m)·x = 0
- sappiamo come si evolve nel tempo la generica variabile x
- Introduzione modellistica al condensatore:
V.d. par. 19.2-19.3- Semplice modello in cui si comporta come
un generatore di tensione variabile
la cui tensione è, istante per istante, proporzionale alla carica su ciascuna 'armatura':
→ VC = Q/C. - La corrente che fluisce verso di esso aumenta o diminuisce
a seconda del verso di scorrimento:
→ dQ = I dt. - Circuito 'RC' e processo di carica e scarica del condensatore.
- Una semplice analisi e l'assunzione della
conservazione dell'energia
permette di associare ad esso una sorta di energia potenziale
(la quale poi 'rispunta fuori' per evetualmente "scaldare una 'pentola' d'acqua": è veramente energia!).
→ Problema nr. 34.5 (poi ci ritorneremo...)
- Semplice modello in cui si comporta come
un generatore di tensione variabile
- Forza di Lorentz e prodotto vettoriale
- forza_di_Lorenz.pdf;
- vecchia dispensa, par. 22.4;
- vecchia dispensa, par. 23.4, solo dopo la (554)
in particolare: (555), (556) e (557); - alcune applicazioni: → Galleria.
- Lezione 35 (25/5, 2h)
-
- Chiarimenti sui problemi in corso,
in particolare:
- risoluzione dei circuiti in corrente continua.
- Sulle unità di misura di capacità e campo magnetico.
- Ancora su prodotto vettoriale.
- V.d. par. 22.4;
- alcune proprietà che risultano palesi
se si usa la tecnica matriciale per il cuo calcolo:
- se i due vettori giacciono nel piano x-y il prodotto vettore è lungo z;
- anticommutazione
- Solidi in rotazione intorno a un asse
Nuovi concetti:- forza e momento della forza;
- inerzia per traslazione (massa) e inerzia per rotazione (momento di inerzia)
- energia cinetica di rotazione
[Nota: in queste pagine la densità di refusi è maggiore di quella usuale. In particolare:- vecF sta per 'F' con sopra la freccia di vettore;
- nella (521) 'ω' al numeratore è chiaramente di troppo;
- 'omega' sta chiaremante per 'ω';
- nella (524) la derivata deconda non è rispetto a v ma rispetto a x;
- nelle (507), (522) e (523) θ rappresenta
l'angolo di rotazione del corpo rigido
e non l'angolo fra forza e 'direzione radiale,' come invece (514) etc.. ]
corpi che scivolano (senza attrito) e che rotolano; auto accelerate e frenate.
→ Galleria.
- Chiarimenti sui problemi in corso,
in particolare:
- Lezione 36 (29/5, 2h)
-
- Problemi in corso, in particolare
- α ↔ τ negli andamenti esponenziali.
- Soluzione di un circuito con metodi di algebra lineare
→ circuito: circ_fig_2_12.png;
→ soluzione mediante R: circuito_probl_2_12.R - Chiarimenti sul problema nr. 34.7 e importante applicazione:
→ ciclotrone (forse a lezione è stato detto anchesincrotrone...)
- Ancora sui momenti di inerzia:
- Su oggetti che rotolano lungo un piano
inclinato:
→ Video in galleria (oltre all'animazione). - Ruolo del volano, ad es. motori e spinning bikes.
- Esempio di calcolo del momento di inerzia:
→ v.d. par. 23.2 ('disco'/'cilindro');
→ problema nr. 36.4 (barretta);
- Su oggetti che rotolano lungo un piano
inclinato:
- Analogie meccanica-probabilità (e 'statistica'(*)):
- media ↔ centro di massa;
- varianza ↔ momento di inerzia rispetto al baricentro.
[(*)Nota: sia in teoria della probabilità che in statistica descrittiva
vengono usati alcuni 'riassunti' che hanno in alcuni casi nomi identici:
- il termine 'media' si usa sia per distribuzioni di probabilità che distribuzioni statistiche;
- anche i termini 'varianza' e 'deviazione standard' si usano in entrambi i casi;
- in termine 'valore atteso' si usa invece soltanto
per distribuzioni di probabilità, con lo stesso significato di 'media'. ]
- Problemi in corso, in particolare
- Lezione 37 (31/5, 2h)
-
- Problemi in corso
- Inferenza (unidimensionale) dei parametri delle distribuzioni
- Dal problema nr. 34.3 (con 3 soli modelli) a una infinità di valori μ
che possono essere responsabili del campione x osservato
(assumendo che σ sia ben nota):
→ f( μ | x, σ); - teorema di Bayes per variabili continue
(attenzione alla notazione!):
f(μ | x, σ) ∝ f(x | μ, σ) · f0(μ); - caso di prior uniforme:
f(μ | x, σ) ∝ f(x | μ, σ);
μ distribuita normalmente- intorno al valore medio delle x;
- con deviazione standard σ/sqrt(n) →:
→ incertezza standard;
→ diminuisce al crescere di n come 1/sqrt(n) [proprietà tipica della statistica!];
- conti dettagliati alla lavagna:
- In analogia, di nuovo per il solo caso di 'flat priors' (prior uniforme)
- dal problema nr. 29.5 all'inferenza di λ
della poissoniana, ovvero
→ da P(λi | n) a f( λ | n ); - dal problema nr. 31.5 all'inferenza di p
della binomiale, ovvero
→ da P(pi | n,x) a f( p | n,x );

- dal problema nr. 29.5 all'inferenza di λ
della poissoniana, ovvero
- Dal problema nr. 34.3 (con 3 soli modelli) a una infinità di valori μ
- Combinazioni lineari di variabili aleatorie indipendenti
- il valore atteso è pari alla combinazione lineare dei valori attesi;
- la varianza è pari alla combinazione lineare delle varianze, con i coefficienti al quadrato;
- non c'è una formula facile e generale per la pdf della
combinazione lineare,
MA se si hanno tanti (n → ∞) termini la distribuzione tende a normale
→ Teorema del Limite Centrale
(mostrato con 'animazione', senza dimostrazione formale)
→ slides: rm23_05_CLT.pdf
→ scripts: sum_square_wave.R; sum_prod_2dice_CLT.R
- Forze inerziali ('fittizie'):
la tendenza naturale a mantenere la velocità costante (rispetto alle stelle fisse)
viene percepita come un 'forza' se il 'supporto' subisce una accelerazione.
- Energia del condensatore
- Ripasso su carica e scarica: galleria qui e qui.
→ Problemi 34.5 e 35.2;
→ v.d. par. 19.4
- Ancora Momento della forza e momento della quantità di moto
- Per come è stato introdotto il momento della forza (v.d. 22.1)
si nota una certa somiglianza con il prodotto vettoriale.
Ma per quanto riguarda la velocità, l'abbiamo considerata solo trasversale al vettore che va dall'asse di rotazione a ciascun punto materiale che ruota. - esperimento in aula con giroscopio;
- condizioni di equilibrio di un corpo rigido: v.d. par. 23.7
→ concetto di 'coppia', praticamente sinonimo (in ambito tecnico...) di momento della forza.
- Per come è stato introdotto il momento della forza (v.d. 22.1)
- Problemi in corso
- Lezione 38 (1/6, 2h)
-
- Problemi in corso
- Propagazione di valori atteri e di varianze
- Dalla combinazione lineare alla linearizzazione:
→ rm23_07_prop.pdf
(vedere anche quanto fatto sull'argomento nel corso di Probabilità e Statistica)
- Dalla combinazione lineare alla linearizzazione:
- Leve ("datemi un punto di appoggio...") v.d. par. 23.8.
- Momento della forza e momento della quantità di moto (trattazione più formale):
- Premessa sulla derivata del prodotto vettoriale:
→ v.d. par. 23.6 (dimostrazione fuori programma); - "Dicesi...":
→ v.d. par. 23.6
→ si noti come il concetto di L non è legato solo al corpo rigido: → (564)-(565); - Forze centrali, velocità aereolare e seconda legge di Keplero
→ seconda_legge_Keplero.pdf
[Nota: a metà pagina compare 'R' al posto di 'r'...]
- Problemi in corso
- Lezione 39 (5/6, 2h)
-
- Problemi in corso, in particolare
- nr. 27.3: diverse 'situazioni fotografiche':
→ attenzione alle cifre significative
(in questo problema era importante la differenza fra |q| e f !)
- nr. 27.3: diverse 'situazioni fotografiche':
- Ancora fluidi:
dispensa_pressione.pdf,
par. 2.13.2, 2.15
(i restanti paragrafi possono servire come ripassi e approfondimenti).- Rapido ripasso.
- Legge di Pascal e applicazioni:
- variazioni di pressione sono propagate in tutti i punti del liquido;
- macchine idrauliche;
- lavoro effettuato da pistoni su liquidi incompressibili.
- Lavoro effettuato da pistoni su fluidi compressibili (cenni)
→ è alla base della 'Termodinamica' (in questo corso abbiamo fatto sostanzialmente termologia);
→ argomentiFSN_pp55.pdf - La scoperta del vuoto (Berti → Torricelli).
- Fluidi incompressibili in movimento (in regime stazionario):
→ Problema nr. 39.3, basato su figura alla lavagna
- Ancora propagazione di incertezze
(→ rm23_07_prop.pdf)
- Propagazione mediante Monte Carlo, confrontata con
propagazione di varianze (+ linearizzazione):
Note:
- la versione 'unif' usa generatori uniformi
al posto di quelli gaussiani
→ la valutazione MC dei valore attesi e deviazioni standard non cambia(!); - per motivi didattici i conti sono stati fatti solo
per il perimetro
→ problema nr. 38.1; - chi avesse problemi con generatori gaussiani se lo può scrivere facilmente: → random_normale.R.
 Le figure mostrano il concetto di correlazione,
ad esempio fra le grandezze derivate
e quelle di partenza (a e b)
Le figure mostrano il concetto di correlazione,
ad esempio fra le grandezze derivate
e quelle di partenza (a e b)
e fra quelle di partenza:
in genere ρ(X,Y) = cor(X,Y) = Cov(X,Y) / [σ(X)·σ(Y)]
→ coefficiente di correlazione- è compreso fra -1 e 1;
- è adimensionale, mentre la covarianza ha le
dimensioni del prodotto di quelle di X e di Y
→ più facilmente percepibile!
- la versione 'unif' usa generatori uniformi
al posto di quelli gaussiani
- Propagazione delle incertezze relative
→ rm23_07_prop.pdf
- Propagazione mediante Monte Carlo, confrontata con
propagazione di varianze (+ linearizzazione):
Note:
- Inferenza di λ della poissoniana (approccio 'pratico')
- inf_lambda.R
da cui risulta (a partire da prior uniforme):- f(λ| n) ha esattamente la stessa espressione matematica
della poissoniana, con il ruolo scambiato di n e λ (!); - E[λ] = n+1;
- σ[λ] = n+1;
- valore modale (moda): eseguire lo script e risolvere il problema nr. 39.6.
- f(λ| n) ha esattamente la stessa espressione matematica
- inf_lambda_bis.R
(variante che mostra ancora meglio la corretta normalizzazione).
- inf_lambda.R
- Problemi in corso, in particolare
- Lezione 40 (7/6, 2h)
-
- Problemi in corso
- Incertezze di misura
- Inevitabilità delle incertezze
- Errore vs incertezza (ISO)
- Cause delle incertezze di misura
('decalogo ISO' )
(Versione pdf, pp. 7-12)
- Ancora sulla distribuzione di Poisson
- Nota tecnica su f(λ|n) con prior uniforme:
→ Gamma(n+1, 1)
- confronto in Galleria (mediante script inf_lambda_gamma.R);
- mediante l'app Probability Distributions:
- Distribuzione predittiva (mediante tecnica di Monte Carlo):
- Problema: n → f(λ|n) → f(nf|n),
con 'nf' numero di conteggi 'futuri'
(ove 'futuro' sta in realtà per 'incerto' — si veda citazione di de Finetti)
- se fossimo certi del valore del valore di λ basterebbe far uso della poissoniana con quel λ;
- ma siccome siamo incerti sul suo valore bisogna tener conto
di tutti i valori possibili, pesandoli con quanto crediamo a ciascuno di essi:
∫0∞ f(nf|λ)·f(λ|n) dλ - risolviamo il problema integrando mediante Monte Carlo:
- si estraggono valori di λ secondo la sua p.d.f.
(usando 'rgamma()' di R, o equivalente); - per ciascun λ estratto, si estrae nf
(usando 'rpois()' di R, o equivalente); - quindi facciamo plot e riassunti 'statistici'.
- si estraggono valori di λ secondo la sua p.d.f.
- Script R: poisson_inf_predictive.R
→ vedi esempio in Galleria
- Problema: n → f(λ|n) → f(nf|n),
con 'nf' numero di conteggi 'futuri'
- Nota tecnica su f(λ|n) con prior uniforme:
→ Gamma(n+1, 1)
- Fluidi incompressibili in movimento regime stazionario:
- Legge di Leonardo.
- Teorema di Bernoulli e consequenze/applicazioni:
- legge di Stevino;
- teorema di Torricelli;
- effetto Venturi.
(Nota: anche se la dimostrazione del teorema di Bernoulli
si basa sull'ipotesi di incoppressibilità alcune consequenze sono
approssimativamente valide anche per fluidi compressibili.)
- Problemi in corso
- Lezione 41 (8/6, 2h)
-
- Problemi in corso
commenti sull'uso dei metodi Monte Carlo
- Oscillatore smorzato, introdotto nella
Lezione 34:
- soluzione analitica richiede alcune conoscenze matematiche;
- Soluzione numerica step by step: istruttiva perché
ci per insegna come risolvere altri problemi 'difficili'.
Script R (con commenti che descrivono in dettaglio il metodo):- molla_xva.R
- molla_xva_smorz.R
→ vedi xt), v(t) e a(t) risultanti in Galleria
- quando la forza può dipendere da tempo, posizione e velocità;
- anche per problemi 3D.
al fine di aumentare l'accuratezza del metodo (o 'algoritmo', come piace dire oggigiorno).
- Ancora ottica geometrica
→ argomentiFSN_pp65-72.pdf ("Problema nr. 2 par. 26.3 (p.44)" sta per "problema nr 40.5")- Ingrandimento angolare (→ problema nr. 28.1): par. 36.2;
- Problema nr. 40.6 → da fare;
- Lunghezza focale e dimensione dell'immagine (p >> f): par. 36.4;
- Angolo di campo (o apertura angolare) (p >> f): par. 36.5
→ Galleria - Lunghezza focale equivalente ('35mm film'): par. 36.7.
[ dimensione dei sensori → Galleria
'foto dell'estintore' citata nel par. 36.7] - Uso telemetrico di una macchina fotografica: par. 36.8-36.9
(nelle formule dove compare y' dovrebbe essere |y'|, come nel par. 36.5)
→ dettagli lasciati come esercizio.
- Ancora sulla distribuzione binomiale
- Nota tecnica su f(p|n,x) con prior uniforme:
→ Beta(x+1, (n-x)+1)
- Valore atteso: E(p) = (x+1)/(n+2) (regola di successione di Laplace)
e limite per x e n molto grandi: E(p) → x/n
('x/n' è invece, in generale, la moda: vedi linee verticali in figura). - confronto in Galleria (mediante script inf_p.R);
- mediante l'app
Probability Distributions:
- 10 prove con 3 successi: f(p|n=10,x=3); momenti
- Valore atteso: E(p) = (x+1)/(n+2) (regola di successione di Laplace)
- Distribuzione predittiva (mediante tecnica di Monte Carlo):
- Problema: (n,x) → f(p|n,x) → f(xf|n,x),
con 'xf' numero di successi 'futuri'
(ove 'futuro' sta in realtà per 'incerto' — si veda citazione di de Finetti)
- se fossimo certi del valore del valore di p basterebbe far uso della binomiale con quel p (e n);
- ma siccome siamo incerti sul suo valore bisogna tener conto
di tutti i valori possibili, pesandoli con quanto crediamo a ciascuno di essi:
∫01 f(xf|n,p)·f(p|n,x) dp - risolviamo il problema integrando mediante Monte Carlo:
- si estraggono valori di p secondo la sua p.d.f.
(usando 'rbeta()' di R, o equivalente); - per ciascun p estratto (e n), si estrae xf
(usando 'rbinom()' di R, o equivalente); - quindi facciamo plot e riassunti 'statistici'.
- si estraggono valori di p secondo la sua p.d.f.
- Script R: binom_inf_predictive.R
→ vedi esempio in Galleria
- Problema: (n,x) → f(p|n,x) → f(xf|n,x),
con 'xf' numero di successi 'futuri'
- Nota tecnica su f(p|n,x) con prior uniforme:
→ Beta(x+1, (n-x)+1)
- Ancora sulle sei scatole e sulla distribuzione binomiale.
→ Inferenza di proporzioni:- inferire la scatola i-ma è equivalente a inferire la proporzione di palline bianche in esso contenute: Hi → pi;
- pi rappresenta chiaramente
la probabilità di estrarre una pallina bianca dalla scatola i-ma; - quando in numero di scatole tende a infinito
→ pi acquista il ruolo di p della binomiale.
→ inferenza di p (vedi sopra).
- video su Youtube...
... con qualche caveat:- circa ok da 2:05 fino a 6:02, a parte il fatto che
i lanci non sembrano proprio random; - un mezzo casino da 6:03 in poi (ove sono dette anche cose corrette, a saperle discernere...)
a farsi un'idea dell'idea del famoso biliardo] - circa ok da 2:05 fino a 6:02, a parte il fatto che
- siccome la posizione del pallino bianca determina
la probabilità che le altre palle finiscano alla sua destra
o alla sua sinitra, inferire la sua posizione da dove sono finite
le palle lanciate è equivalente a inferire p della binomiale (vedi sopra).

- Problemi in corso
Torna su — Galleria — Home
Torna su — Galleria — Home
Torna su — Galleria — Home
Torna su — Galleria — Home
Torna su — Galleria — Home
Torna su — Galleria — Home
Torna su — Galleria — Home
Torna su — Galleria — Home
Torna su — Galleria — Home
Torna su — Galleria — Home
Torna su — Galleria — Home
Torna su — Galleria — Home
Torna su — Galleria — Home
Torna su — Galleria — Home
Torna su — Galleria — Home
Torna su — Galleria — Home
Torna su — Galleria — Home
Torna su — Galleria — Home
Torna su — Galleria — Home
Torna su — Galleria — Home
Torna su — Galleria — Home
Torna su — Galleria — Home
Torna su — Galleria — Home
Torna su — Galleria — Home
Torna su — Galleria — Home
Torna su — Galleria — Home
Torna su — Galleria — Home
Torna su — Galleria — Home
Torna su — Galleria — Home
Torna su — Galleria — Home
Torna su — Galleria — Home
Torna su — Galleria — Home
Torna su — Galleria — Home
Torna su — Galleria — Home
Torna su — Galleria — Home
Torna su — Galleria — Home
Torna su — Galleria — Home
Torna su — Galleria — Home
Torna su — Galleria — Home
Torna su — Galleria — Home
Torna su — Galleria — Home
Torna alla pagina del corso