



Next: Raccomandazioni ISO/BIPM
Up: Errori e incertezze di
Previous: Introduzione
Indice
Figura 1:
Dalle osservazioni alle ipotesi. La relazione
fra valore della grandezza e teoria sta ad indicare che in genere
le grandezze hanno significato soltanto all'interno di una teoria o
un modello.
 |
Cerchiamo di capire quali sono le ragioni di fondo che,
nella ricerca scientifica, conducono ad uno stato di incertezza.
La figura 1
schematizza
l'attività del fisico o di qualsiasi altro ricercatore.
Dai dati sperimentali si cerca di determinare il valore
di una certa grandezza o di stabilire quale teoria descrive meglio
i fenomeni osservati.
In realtà entrambi i processi
possono essere visti come due aspetti dello stesso problema:
come passare dalle osservazioni alle ipotesi. Infatti
i due problemi possono essere riformulati nei seguenti modi:
- A
- quali valori sono (più)
compatibili con la definizione della grandezza oggetto
della misura, avendo letto certi numeri sugli strumenti
(e subordinatamente a tutte le conoscenze sugli strumenti
e sulla grandezza in questione)?
- B
- quale teoria è (più) compatibile con i fenomeni osservati
(e subordinatamente alla credibilità della teoria
basata su argomenti formali, estetici e di
semplicità1)?
La sola differenza fra i due processi di apprendimento
è che, mentre nel secondo caso si ha a che fare
generalmente con un piccolo numero
di ipotesi, nel primo caso il numero di ipotesi è virtualmente
infinito (le grandezze assumono i valori numerici con continuità,
almeno in linea di principio).
Il motivo per cui non si arriva mai alle
condizioni ideali di certezza, ovvero
tali che soltanto una delle
tante (o infinite) ipotesi sia da ritenersi vera e tutte le altre
false, può essere compreso analizzando lo schema che segue.
- A:
- Per quanto riguarda la determinazione del valore di una grandezza
si dice comunemente che l'incertezza sia
dovuta ad inevitabili ``errori di
misura'' (fluttuazioni della risposta, calibrazione degli strumenti,
condizioni ambientali non perfettamente note, etc.);
- B:
- Quando si tratta di una teoria possiamo distinguere
due casi:
- (B
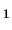 )
)
- La legge è probabilistica, ovvero ``le osservazioni
non sono una mera conseguenza logica della teoria''. Un classico
esempio è quello della genetica. Un esempio più semplice
è quello del lancio di una moneta.
E' noto dal calcolo delle probabilità
che, lanciando una moneta regolare,
le due sequenze di testa (T) e croce (C)
| T T T T T T T T T T T T T T T T T T T T T T T T T |
(1) |
| T T C C C C C T T T T C T T C C T T T C T C T T C |
(2) |
hanno la stessa probabilità. Quindi sarà impossibile
arrivare a conclusioni
certe sulla regolarità di una moneta ignota
pur avendo osservato una sequenza di lunghezza
arbitraria2;
- (B
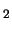 )
)
- La legge è deterministica. Non è difficile
convincersi come
questa denominazione
sia valida
solo in linea di principio.
Infatti, in tutti i casi, ``le osservazioni dipendono
anche da molti altri fattori esterni alla teoria'',
siano essi condizioni
iniziali e ambientali, errori sperimentali, e così
via. Ne segue quindi che
le inevitabili incertezze su questi fattori rendono la relazione
teoria
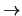 osservazione di tipo probabilistico
anche in questo caso.
osservazione di tipo probabilistico
anche in questo caso.




Next: Raccomandazioni ISO/BIPM
Up: Errori e incertezze di
Previous: Introduzione
Indice
Giulio D'Agostini
2001-04-02

