Introduzione

Scrivendo questa nota ho cercato di venire incontro a tutti coloro che trovano motivi di insoddisfazione nella trattazione dei cosiddetti ``errori di misura'': studenti poco convinti di quanto viene loro insegnato, in quanto spesso privo di consistenza logica e di corrispondenza con l'esperienza di laboratorio; laureandi e neolaureati che, inseriti nella ricerca, sia pura che applicata, sperimentano l'inadeguatezza dei metodi appresi per far fronte alle analisi complesse che si presentano e sono confusi dalle tante ``ricette monouso'', spesso contraddittorie, che trovano in libri, note tecniche e articoli; ricercatori che, delusi dall'incongruenza fra teoria e pratica, affermano francamente di non usare la statistica o, addirittura, di non essere interessati al ``calcolo degli errori''; docenti universitari che si rendono conto, specialmente se interagiscono con ambienti di ricerca internazionali, che le cose stanno cambiando ed in effetti provano a riaggiornare i corsi, pur ostacolati dalla mancanza di testi validi e da colleghi con i quali devono interagire per uniformità di programma; insegnanti delle scuole medie superiori in dubbio su come comportarsi nei corsi di laboratorio e indecisi se affrontare o meno il discorso delle incertezze di misura, con quali metodi e a quale livello.

Questo lavoro è basato sull'esperienza acquisita nella ricerca (nel campo della Fisica Subnucleare) e nell'insegnamento, arricchita da interazioni, dirette o indirette, con metrologi e probabilisti, da discussioni con colleghi di diverse nazionalità e dal feedback ricevuto in seminari e corsi di perfezionamento impartiti in Italia e all'estero. Negli ultimi anni ho anche beneficiato di contatti con gli insegnanti dell'AIF (Associazione per l'Insegnamento della Fisica) di Roma e con gli studenti del Corso in Perfezionamento in Didattica della Fisica.

La trattazione non pretende di avere nessun carattere di completezza. Ha però il vantaggio di offrire una vista d'insieme che permette al lettore la possibilità di confrontare i metodi che vengono criticati con quento viene proposto. E' pertanto opportuno fare alcuni chiarimenti preliminari sul taglio del lavoro e sulle conoscenze che si presuppongono da parte del lettore.

• L'impostazione della parte di rassegna critica è deliberatamente provocatoria, con la speranza di suscitare le reazioni di chi non condivide questo punto di vista e di innescare un dibattito costruttivo su eventuali temi controversi dal quale beneficiare tutti, studenti in primo luogo.
• Una trattazione delle incertezze di misura che fornisca soltanto formule pratiche, anche se ritenute ragionevoli dai più e supportate dalle raccomandazioni delle massime organizzazioni di metrologia, costituisce una costruzione vacillante se non si presenta in modo coerente, con delle basi sulle quali eventualmente convenire e dalle quali derivare le consequenze logiche.
• Le basi di partenza di questa impostazione sono semplicemente:
  1. la constatazione dell'inevitabile stato di conoscenza incertezza cui l'induzione dà luogo (ricollegabile alla famosa ``critica di Hume'' di tale processo);
  2. l'accettazione della validità del concetto di probabilità per classificare la plausibilità delle affermazioni quando si è in stato di incertezza (riconducibile alla visione originale di probabilità la quale è stata ripresa e consolidata dopo i primi decenni di questo secolo ed è attualmente nota come ``soggettiva'' o ``bayesiana'').
  Una volta accettati questi presupposti, tutto il resto viene derivato come conseguenza logica. Si tratta soltanto di formalismi, approssimazioni ed eventuali scorciatoie per semplificare la trattazione dei normali problemi di routine.
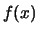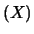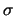• Si presuppone che il lettore sia già stato esposto alla problematica dell'incertezza di misura e che abbia una conoscenza elementare del calcolo delle probabilità. In particolare, si assume che egli abbia le nozioni di base per trattare le variabili casuali (``$f(x)$'', `` E$(X)$'', ``$\sigma$'', distribuzione uniforme e normale). Alcuni di questi concetti verranno reinterpretati alla luce della probabilità soggettiva, ma i risultati formali del calcolo delle probabilità sono gli stessi dell'approccio convenzionale.
• Anche se il concetto di funzione densità di probabilità è importante per capire il ragionamento che si svilupperanno, la parte applicativa farà uso solo di deviazioni standard, in quanto l'ipotesi di normalità (distribuzione gaussiana) è spesso soddisfacentemente soddisfatta nei casi di routine. Anche il teorema di Bayes, sul quale sarà basato il processo di aggiornamento della conoscenza, sarà scavalcato con argomentazioni intuitive.
• Venendo alle applicazioni della cosiddetta inferenza bayesiana all'incertezza di misura, saranno mostrate procedure alternative a quelle criticate nella parte iniziale. Molti riconosceranno metodi che già conoscono e usano, spesso visti però come una tecnica ad hoc per risolvere un problema particolare.
• Infine verranno dati dei suggerimenti per la didattica.
• Il lavoro si conclude con un'appendice in cui vengono riportati alcuni argomenti accessori e illustrate alcune semplici esperienze.

Ovviamente sarò felicissimo di avere scambi di idee con tutti coloro che avranno critiche, commenti o proposte sul testo.

Giulio D'Agostini Roma, Maggio 1998

Questa versione corretta ha beneficiato dei commenti di Maria Grazia Ianniello e dell'attentissima lettura di Marco Schioppa.
Roma, Gennaio 1999