- ...
semplicit\`a1
- Si vedrà come queste postille di
subordinazione delle conclusioni scientifiche a conoscenze e
``pregiudizi'' a priori giocano un ruolo fondamentale nei
processi di misura e nell'accettazione di teorie da parte della
comunità scientifica.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
arbitraria2
- Ma dopo l'osservazione della prima
delle sequenze
è forte il sospetto
che si tratti di una moneta con due teste, qualora
ci siano delle buone ragioni per far sorgere un simile dubbio
(ad esempio non si à modo di verificare direttamente
la regolarità della moneta).
Il concetto di probabilità servirà a quantificare
il grado di tale sospetto.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
particolare''3
- ``Grandezza particolare'' (altezza di
una certa torre, massa dell'elettrone,
accelerazione di gravità a Roma)
è in contrapposizione con ``grandezza generale''
(lunghezza, massa, accelerazione).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
vero4
- Si capisce quindi come la definizione
di valore vero come
``quello che si otterrebbe
dopo una serie infinita di misure con strumentazione
ideale'' non è migliore di quella ISO, anzi, questa dà
l'illusione che questo valore sia, almeno idealmente, unico,
mentre la definizione ISO tiene conto che le misure vengono
eseguite in condizioni reali e con tutte le cause
di incertezza che saranno elencate in questo paragrafo.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... simulazione5
- Non ci sarebbe alcun bisogno
di simulare il processo al computer, dato che la soluzione
può essere ottenuta analiticamente mediante il
calcolo delle probabilità, ma l'esperienza mi insegna
che le simulazioni possono essere più convincenti per alcune persone.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
altri6
- Ci si potrebbe chiedere: come mai questo processo
non porta ad un collasso? Semplicemente perché nei laboratori
non si seguono queste regole e, invece di nascondere la testa
nella sabbia degli errori massimi, si cerca di ricalibrare
in continuazione strumenti e procedure. Questo è
quanto dovrebbe imparare subito
anche lo studente
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
puerile7
- Questo aspetto psicologico non
riguarda soltanto gli studenti. Non è raro vedere anche
nella ricerca avanzata risultati in sorprendente accordo
fra di loro o con predizioni teoriche nonostante le loro
enormi barre di incertezza, o fisici sperimentali preoccupati
se i loro valori differiscono di un paio di
deviazioni standard da una ``solida predizione'' o da un
risultato precedente.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... lettura8
- A volte lo si sente chiamare
anche errore di sensibilità, o addirittura semplicemente
``sensibilità'' (in una nota per studenti si legge testualmente:
``l'indeterminazione su tali grandezze può essere presa pari alla
sensibilità del termometro impiegato, ovvero mezza tacca'').
In questo caso ``sensibilità'' starebbe per ``risoluzione''
(vedi norma DIN 1319, 2, 9, che incontreremo fra poco). E' raccomandabile
utilizzare il termine ``sensibilità'' per indicare ...
la sensibilità, ovvero,
detto alla buona, ``il rapporto fra la variazione della risposta
e la variazione dello stimolo''.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... divisioni.''9
- Essere praticamente sicuri che
il valore sia entro il 1/5 di divisione, vuol dire
che, se ci si sforza al interpolare al meglio, ci
si aspetta una deviazione standard dell'errore di
lettura di circa
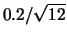 divisioni,
compatibile al valore di
divisioni,
compatibile al valore di
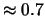 che si osserva
sperimentalmente.
che si osserva
sperimentalmente.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
tacche10
- Perché non cambiare strumento?
Domanda legittimissima. Il problema è che questo non è sempre possibile.
Quindi è importante, all'occorrenza, imparare a sfruttare tutta
la potenzialità degli strumenti a disposizione. Queste dovrebbero
essere le regole del gioco
sulle quale sviluppare un corso di teoria
e pratica di valutazione delle incertezze di misure.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... secondo11
- Si noti inoltre che, quando si misura
una grandezza fisica (
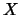 ) in funzione del tempo (
) in funzione del tempo (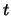 ), non ha molto
senso parlare di errori su
), non ha molto
senso parlare di errori su 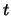 e su
e su 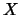 ,
in quanto ogni differenza dell'istante di lettura dal
tempo nominale si rifletterà in un errore sulla
grandezza fisica. Quindi, ai fini del risultato finale,
è più che ragionevole attribuire tutto l'errore a
,
in quanto ogni differenza dell'istante di lettura dal
tempo nominale si rifletterà in un errore sulla
grandezza fisica. Quindi, ai fini del risultato finale,
è più che ragionevole attribuire tutto l'errore a 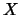 e considerare
e considerare 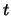 esente da errore (si veda anche
il paragrafo 16.4.2).
esente da errore (si veda anche
il paragrafo 16.4.2).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Quinn12
- T.J. Quinn, ``The
beam balance as an instrument for very
precise weighing'', Meas. Sci. Technol., 3(1992), 141.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
massimi13
- Qualcuno prova a trasformare ``errori massimi''
in ``errori statistici'', considerando
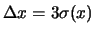 e, nella direzione opposta,
e, nella direzione opposta,
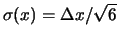 (assumendo una distribuzione uniforme
del valore vero di
(assumendo una distribuzione uniforme
del valore vero di 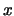 entro
entro
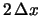 ). La seconda trasformazione
è ragionevolissima se veramente si crede che
). La seconda trasformazione
è ragionevolissima se veramente si crede che 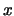 possa assumere qualsiasi valore entro
possa assumere qualsiasi valore entro
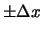 ,
sebbene questo credere
sia in contrasto con le interpretazioni usuali di probabilità.
La trasformazione inversa (
,
sebbene questo credere
sia in contrasto con le interpretazioni usuali di probabilità.
La trasformazione inversa (
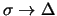 ), con
l'uso successiva delle propagazioni lineari è invece assurdo
in quanto in contrasto con le proprie credenze (gli
errori massimi assumono, tacitamente, indifferenza entro
), con
l'uso successiva delle propagazioni lineari è invece assurdo
in quanto in contrasto con le proprie credenze (gli
errori massimi assumono, tacitamente, indifferenza entro
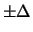 ).
).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
completa,14
- Un altro punto molto critico, ma su cui
non entreremo, è quello legato ai cosiddetti ``test di ipotesi''.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
osservazione''15
- Ho sentito questa espressione dal
neurologo Sergio Della Sala
durante la conferenza annuale del CICAP (Comitato Italiano
per il Controllo delle Affermazioni sul Paranormale), Padova, Novembre 1997.
L'originale dovrebbe essere di Umberto
Eco, forse in ``Kant e l'ornitorinco''...
Il significato che attribuisco a questa espressione in questo contesto
sarà chiaro a partire dal paragrafo 13:
la mera osservazione empirica ("un numero su un display'')
non accresce la Conoscenza, se questa informazione viene avulsa
dal contesto di ``credenze''
che contornano misurando, strumento di misura e processo di misura.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
Kant16
- E' molto espressivo il commento di Bruno de
Finetti sull'insuccesso di Kant a far fronte alla critica di Hume:
``Ma le reazioni contro ogni chiarificazione intelligente
sono sempre pronte e pieno di sacro zelo, in difesa della sacra
ottusità: ecco il povero Kant affannarsi
a tamponare la falla aperta da Hume ed a rabberciare la sconnessa
fabbricazione tradizionale, dove il ragionamento induttivo si vuole a forza
ricollegato e inserito, al pari di quello
deduttivo,
nelle strutture anguste della logica del certo''.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... frequenza''17
- Assumiamo che il lettore sia al corrente
delle ``definizioni'' standard,
quelle che si studiano comunemente
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...illegittima18
- Nessun testo serio
di probabilità convenzionale riporta la (13).
Si parla invece di ``intervallo di fiducia'', che ha
però tutt'altro significato, anche se diversi testi e
molti insegnanti ne suggeriscono un'interpretazione probabilistica.
Senza entrare nei dettagli, ad uso di chi è familiare
con questi concetti, chiariamo brevemente come la ragione
di fondo di questa contraddizione sia da ricercarsi nel rifiuto
di accettare l'interpretazione di probabilità come grado
di fiducia.
Il concetto frequentistico
di intervallo di fiducia è quindi una sorta
di forzatura inventata
per caratterizzare l'incertezza in un modo consistente
con la visione frequentistica di probabilità (vedi nel seguito).
Purtroppo - è un dato di fatto - tentare di classificare
lo stato di incertezza evitando il concetto di probabilità
conduce a fraintendimenti.
Emblematico di questi ben noti problemio è quanto risultava
da una tavola rotonda fra statistici americani alla quale ho assistito
in occasione del loro congresso annuale del 1996:
``i nostri studenti
non capiscono gli intervalli di fiducia''.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... appreso''19
- Questa osservazione
deriva dalla constatazione che, come detto, la maggior parte
dei fisici interpellati sia convinta in buona fede
della legittimità della (13), pur sostenendo
che la probabilità sia il ``limite della frequenza''.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ``coerente''20
- Senza entrare
nel dettaglio, chiariamo brevemente
cosa si intende per ``coerente'' (o ``reversibile''): una volta
fissate le quote di scommessa pro e contro l'evento
(proporzionali alla probabilità dell'evento e del suo opposto),
deve essere indifferente
allo scommettitore il verso della scommessa:
se c'è una netta
propensione pro, vuol dire che bisogna alzare la quota in favore
dell'evento;
nel caso opposto bisogna alzare
l'altra quota. Il rapporto
delle quote, in condizione di indifferenza sul verso da scegliere,
è una valutazione del
rapporto delle probabilità.
Quindi il valore della probabilità
è dato dalla quota di scommessa sull'evento divisa per il
totale delle quote.
Si può dimostrare che la coerenza fornisca (come teoremi!)
le regole sintattiche
della probabilità analoghe a quelle espresse dai ben noti assiomi.
Inoltre da essa si deriva anche la relazione che lega probabilità
condizionata alla probabilità congiunta evento-condizionante
e a quella del condizionante (mentre nell'approccio assiomatico
questa formula è una definizione, con il risultato
di produrre conseguenze paradossali). Un'altro aspetto importante
della coerenza è che essa fa sì che le valutazioni soggettive
siano tutt'altro che ``arbitrarie''.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
l'aggiornamento21
- Ma anche in questo caso si è imparato
qualcosa, cioè che il termometro non funziona...
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
critica22
- Molto spesso si pensa che l'unico metodo scientifico
valido sia quello della falsificazione.
Non ci sono dubbi che, se una teoria
non è in grado di descrivere i risultati di
un esperimento,
essa vada scartata o modificata. Ma poiché non è possibile
dimostrare la certezza di una teoria, diventa impossibile decidere
fra tutte le (infinite) ipotesi non falsificate.
Il metodo probabilistico
permette di fornire una scala di credibilità a tutte
le ipotesi considerate (o rapporti di credibilità fra ogni
coppia di ipotesi).
Un caso in cui il metodo
di falsificazione è completamente inadeguato
è quello relativo agli incertezze di misura.
Infatti, prendendo alla lettera
tale metodo, si sarebbe autorizzati soltanto a
verificare se il valore osservato sullo strumento
è compatibile o no con un valore
vero, niente di più. Si capisce come, con queste
premesse, non si possa fare
molta strada.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... osservare23
- Attenzione a non confondere la probabilità
di osservare un certo valore
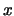 , subordinatamente ad un certo valore
di
, subordinatamente ad un certo valore
di 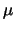 , con la probabilità del valore che è stato
effettivamente osservato. Essendo questo un numero certo
(a meno di non essere ubriachi), ad esso non si applica il
concetto di probabilità.
Così pure, si faccia attenzione a non chiamare
, con la probabilità del valore che è stato
effettivamente osservato. Essendo questo un numero certo
(a meno di non essere ubriachi), ad esso non si applica il
concetto di probabilità.
Così pure, si faccia attenzione a non chiamare
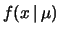 ``probabilità che
``probabilità che 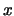 venga da
venga da 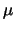 '' (il nome corretto - trascurando
il fatto inessenziale che si tratta di una densità di probabilità e non
di una probabilità - è ``probabilità di
'' (il nome corretto - trascurando
il fatto inessenziale che si tratta di una densità di probabilità e non
di una probabilità - è ``probabilità di 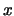 ,
dato un certo valore
,
dato un certo valore 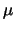 '',
che è chiaramente ben altra cosa!).
'',
che è chiaramente ben altra cosa!).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
dell'osservazione24
- Si noti l'uso dello stesso simbolo
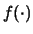 per indicare funzioni di diverse variabili, anche se
sarebbe formalmente più corretta una scrittura della
(16) del tipo:
con
per indicare funzioni di diverse variabili, anche se
sarebbe formalmente più corretta una scrittura della
(16) del tipo:
con
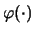 ,
,
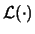 e
e
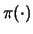 che ricordano dal nome, rispettivamente, la finale,
la verosimiglianza (in inglese likelihood) e la
prior.
che ricordano dal nome, rispettivamente, la finale,
la verosimiglianza (in inglese likelihood) e la
prior.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Poincar\'e25
- H. Poincaré, ``Scienza e Ipotesi'',
molto interessante il capitolo XI sul calcolo
delle probabilità.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... misura26
- Le prior non devono mai sparire
completamente dalla mente, ma devono servire a vigilare
attentamente il flusso dei dati e intervenire
al minimo sospetto che qualcosa non vada!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
Bayes27
- Una prior uniforme e una verosimiglianza gaussiana
producono, in virtù della (17),
il seguente risultato:
in cui nell'ultimo passaggio sono stati invertiti
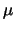 e
e 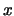 , al fine di ricordare che la variabile
della nuova funzione è
, al fine di ricordare che la variabile
della nuova funzione è 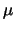 e non più
e non più 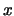 (questo
diventa il parametro che dà il centro della distribuzione).
Ne segue che il valore vero è distribuito intorno
al valore osservato secondo una gaussiana avente la stessa
deviazione standard della verosimiglianza:
(questo
diventa il parametro che dà il centro della distribuzione).
Ne segue che il valore vero è distribuito intorno
al valore osservato secondo una gaussiana avente la stessa
deviazione standard della verosimiglianza:
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... tipo28
- Il fatto che il solo valore
della media aritmetica sia in grado di produrre una inferenza
statistica della stessa qualità dei singoli valori osservati
è legato al concetto statistico di ``sufficienza''.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... media29
- Si ricorda che,
ai fini del calcolo pratico essa è valutata come:
ove
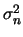 sta ad indicare, secondo la convenzione delle
calcolatrici tascabili,
che la varianza è calcolata come media dei quadrati
degli scarti.
sta ad indicare, secondo la convenzione delle
calcolatrici tascabili,
che la varianza è calcolata come media dei quadrati
degli scarti.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... trascurabili30
- In realtà questo è una
condizione non necessaria, legata ad un modo semplicistico di vedere
le cose: anche se ci sono incertezze sulle ascisse, queste possono
essere riflesse su quelle delle ordinate e la soluzione pratica non cambia.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... indirette31
- Vedremo come entrano in gioco anche
più per
valutare effetti di errori sistematici di misure dirette.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
riproducibilità.32
- La Guida ISO
definisce reproducibility (of results of measurements)
``closeness of the agreement between the results of measurements of
the same measurand carried out under changed conditions of measurement''
(i risultati si intendono già corretti per
eventuali errori sistematici noti).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
gaussiana33
- In realtà non c'è bisogno che la distribuzione
sia normale, in quanto faremo uso soltanto delle proprietà generali
della varianza. Anche dal punto di vista pratico, è più frequente
il caso di una distribuzione uniforme o triangolare.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
accorgimento34
- Ad esempio un voltmetro può
essere calibrato in modo relativo (rispetto al valore di fondo scala)
utilizzando un partitore di precisione: ogni deviazione dalla
linearità sarà imputato al comportamento del voltmetro e
la lettura potrà essere corretta. Per fare un buon
partitore economico è sufficiente prendere una ventina di
resistori all'1% tutti uguali e presi nuovi dalla stessa
striscia con cui sono confezionati.
Le variazioni relative di resistenza
sono ben inferiori all'1% e la loro combinazione riduce ancora di più
le incertezze relative.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...lineare35
- Questo è un punto importante, ma sul
quale purtroppo non possiamo entrare in dettaglio.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... quantity36
- Per
``grandezza d'ingresso'' la Guida ISO intende tutte
le grandezze che contribuiscono alla valutazione del valore
della grandezza di interesse (costanti di calibrazione, parametri di
influenza, valori tabulati, risultati di esperimenti precedenti, etc.).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... riferimento''37
- I valori che
seguono, la formula (39) e la tabella 2
sono presi da
F. Kohlrausch,
``Praktische Physik'', B.G. Teubner Stuttgart 1986. La
sezione 72 sulla densità dell'aria è curata da M. Kochsieck
dell'istituto tedesco di metrologia di Braunschweig.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... infatti38
- Si noti che questa espressione è valida
per variabili continue. Per variabili discrete equispaziate
fra
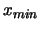 e
e 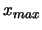 , la formula esatta
è
che tende alla deviazione standard del caso continuo quando
, la formula esatta
è
che tende alla deviazione standard del caso continuo quando
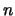 è molto grande. Comunque, già per
è molto grande. Comunque, già per  il fattore
correttivo è del 20% e per
il fattore
correttivo è del 20% e per  è del 10%.
è del 10%.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
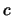 39
39
- Per
quanto riguarda il numero di cifre significative,
si noti come ne sia stata aggiunta una in più rispetto
alle regolette usuali. Esse verranno aggiustate in seguito
alla luce di
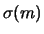 e di
e di 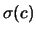 . Nel caso in
cui l'esperienza non preveda un'analisi completa delle incertezze
di misura sarebbe stato sufficiente scrivere
. Nel caso in
cui l'esperienza non preveda un'analisi completa delle incertezze
di misura sarebbe stato sufficiente scrivere
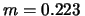 m kg
m kg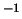 e
e 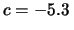 cm.
cm.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
soddisfacente40
- Le piccole differenze
numeriche sono dovute
all'uso della formula approssimata per il braccio di leva.
Corretto per il fattore
esso diventa 0.180kg, da cui ne segue un risultato
praticamente identico a quello ottenuto mediante programma:
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 1.000 kg41
- Si noti come nella propagazione
non si debba tener conto di un'eventuale incertezza sulla massa
se essa è simile a quella dei pesetti con i quali sono
state effettuate le misure, in quanto questo contributo è già compreso
in
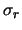 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... informatiche42
- Questa non è una sceneggiata. Così come
è vero che
i dati sperimentali sono stati effettivamente presi
da studenti e che l'analisi grafica l'ho fatta io prima
di verificare i risultati al computer,
è anche vero che,
in data 25 aprile 1998, al momento
di completare questo esercizio,
mi sono accorto che il programma dava risultati sbagliati,
in quanto dimenticava il termine di correlazione.
Si trattava di un programma sviluppato da studenti
durante una borsa di collaborazione, i cui risultati
erano stati testati (con eccezione delle estrapolazioni,
perché sembrava la parte meno critica e sulle quali erano
state convenute le formule da usare).
Il valore di 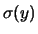 consistente con i risultati del
fit dello stesso programma sarebbe dovuto essere
consistente con i risultati del
fit dello stesso programma sarebbe dovuto essere 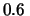 mm.
mm.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... baricentro.43
- Come abbiamo già fatto notare,
il sistema del baricentro è molto conveniente, in quanto
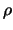 si annulla. L'espressione di
si annulla. L'espressione di 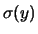 è particolarmente
semplice e istruttiva:
Si riconosce la combinazione in quadratura dell'incertezza
dovuta all'intercetta con quella del coefficiente angolare
``proiettata'' ad una distanza
è particolarmente
semplice e istruttiva:
Si riconosce la combinazione in quadratura dell'incertezza
dovuta all'intercetta con quella del coefficiente angolare
``proiettata'' ad una distanza
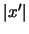 dal baricentro.
dal baricentro.
Siccome 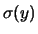 deve essere invariante per traslazioni,
antitrasformando da
deve essere invariante per traslazioni,
antitrasformando da 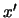 a
a 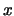 , otteniamo la formula
, otteniamo la formula
Si vede quindi come la previsione sull'ordinata abbia
una precisione che è massima in corrispondenza del baricentro
dei punti e si deteriora quando ci si allontana dalla regione
in cui sono state effettuate le misure.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
differenze44
- Naturalmente, per
ottenere la massima accuratezza sulla precisione dei parametri
sarebbe stato meglio misurare individualmente ciascuno
dei pesetti, al fine di ridurre
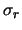 , ma a questo livello
non ne vale la pena.
, ma a questo livello
non ne vale la pena.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
sperimentali''
45
- M. Severi,
``Introduzione alla esperimentazione fisica'',
Zanichelli, 1985.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
l'apprendimento46
- A mio giudizio, sapere ``tutto'' prima
di andare in laboratorio può essere poco stimolante in quanto
elimina l'``effetto sorpresa''.
Trovo spesso
utile informare gli studenti soltanto su come fare la misura
ma non su quello che verrà fuori, specialmente se il risultato
può essere a prima vista controintuitivo.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
uguali47
- Ad esempio, dovendo stimare una temperatura
ambiente, se dicono
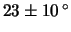 C si scommette pro, se dicono
C si scommette pro, se dicono
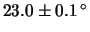 C si scommette contro, e così via
finché non si converge ad risultato di indifferenza che definisce
un'intervallo di credibilità al 50%.
C si scommette contro, e così via
finché non si converge ad risultato di indifferenza che definisce
un'intervallo di credibilità al 50%.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
tipo48
- Questa limitazione cade se si effettuano misure
su grandezze fisiche aventi valori prossimi fra di loro
e siamo interessati soltanto alle loro differenze.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
rapida49
- Come controesempio si immagini di avere un milione
di variabili indipendenti, aventi distribuzione poissoniana
con
 . La somma delle variabili è
ancora poissoniana, con
. La somma delle variabili è
ancora poissoniana, con  , ben lontana da una gaussiana
(in questo caso servono 10-20 milioni di contributi).
, ben lontana da una gaussiana
(in questo caso servono 10-20 milioni di contributi).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
gaussiana50
- Qualcuno potrebbe parlare di ``dimostrazione
sperimentale'' della proprietà delle medie. Ma a rigore
questa non è una dimostrazione. Meglio parlare di
``accordo con le previsioni''. E' vero però che questo accordo
serve a rafforzare la convinzione che le valutazioni
a priori siano corrette.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
![$\displaystyle f(x\,\vert\,\mu) \propto
\exp{\left[-\frac{(x-\mu)^2}{2\,\sigma^2_r}\right]}$](img176.png)
![$\displaystyle \exp{\left[-\frac{(\mu-x)^2}{2\,\sigma^2_r}\right]}\,,$](img177.png)
![$\displaystyle f(\mu\,\vert\,x) = \frac{1}
{ \sqrt{2\,\pi} \sigma_r}
\exp{\left[-\frac{(\mu-x)^2}{2\,\sigma^2_r}\right]}\,.$](img178.png)
e
, la formula esatta è
che tende alla deviazione standard del caso continuo quando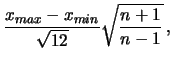
è molto grande. Comunque, già per
il fattore correttivo è del 20% e per
è del 10%.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .39
e di
. Nel caso in cui l'esperienza non preveda un'analisi completa delle incertezze di misura sarebbe stato sufficiente scrivere
m kg
e
cm.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .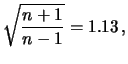
mm
.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .consistente con i risultati del fit dello stesso programma sarebbe dovuto essere
mm.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .si annulla. L'espressione di
è particolarmente semplice e istruttiva:
Si riconosce la combinazione in quadratura dell'incertezza dovuta all'intercetta con quella del coefficiente angolare ``proiettata'' ad una distanza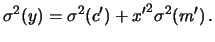
dal baricentro.
deve essere invariante per traslazioni, antitrasformando da
a
, otteniamo la formula
Si vede quindi come la previsione sull'ordinata abbia una precisione che è massima in corrispondenza del baricentro dei punti e si deteriora quando ci si allontana dalla regione in cui sono state effettuate le misure. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . ., ma a questo livello non ne vale la pena.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .C si scommette pro, se dicono
C si scommette contro, e così via finché non si converge ad risultato di indifferenza che definisce un'intervallo di credibilità al 50%.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. La somma delle variabili è ancora poissoniana, con
, ben lontana da una gaussiana (in questo caso servono 10-20 milioni di contributi).
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .