



Next: Scorciatoia al ragionamento bayesiano:
Up: Dalla probabilità degli effetti
Previous: Probabilità iniziale e probabilità
Indice
Molti possono rimanere
perplessi al pensiero che le conclusioni scientifiche
possano dipendere dal ``pregiudizio'' sulla grandezza fisica
(``pregiudizio'' ha correntemente un significato
prevalentemente negativo, ma in realtà
significa semplicemente un giudizio a priori, basato su una
esperienza precedentemente acquisita). Non potendo
addentrarci con la
dovuta profondità in questo aspetto interessante del problema,
aggiungiamo alcune note esplicative. Premettiamo una
citazione di Poincaré25,
non tanto per tentare di convincere
mediante il principio di autorità, quanto perché il concetto è
espresso con molta chiarezza.
``Un effetto potrebbe essere prodotto dalla causa 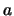 o dalla causa
o dalla causa 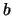 . L'effetto è appena stato osservato.
Ci domandiamo la probabilità che sia dovuto alla causa
. L'effetto è appena stato osservato.
Ci domandiamo la probabilità che sia dovuto alla causa 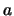 .
Questa è una probabilità di causa a posteriori.
Ma non la potrei calcolare, se una convenzione più o
o meno giustificata non mi dicesse in anticipo qual'è
la probabilità a priori che la causa
.
Questa è una probabilità di causa a posteriori.
Ma non la potrei calcolare, se una convenzione più o
o meno giustificata non mi dicesse in anticipo qual'è
la probabilità a priori che la causa 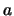 entri in gioco''.
entri in gioco''.
Detto altrimenti, il contributo delle probabilità a priori è cruciale
nei problemi di inferenza. Questo non deve però spaventare, in quanto:
- è assolutamente ragionevole trarre le conclusioni
non in modo meccanico, ma alla luce della ragione;
- nelle misure di routine l'intervallo di
``accettanza a priori'' dei possibili
valori è talmente ampio, rispetto alla larghezza della
verosimiglianza, che in pratica è come se
tutti i possibili valori di
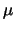 fossero
ritenuti a priori ugualmente possibili. La
prior viene allora ad essere assorbita
nella costante di normalizzazione:
fossero
ritenuti a priori ugualmente possibili. La
prior viene allora ad essere assorbita
nella costante di normalizzazione:
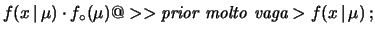 |
(17) |
- quando invece questo non è vero (ad esempio se si usa uno strumento
con il quale non si ha confidenza, oppure se
si deve valutare il risultato di una misura eseguita
da persona inesperta) è assolutamente legittimo credere più
ai propri pregiudizi che al dato empirico. E' infatti molto più
facile che uno studente sbagli la misura che scopra una nuova
legge fisica. Poincaré fa un bell'esempio di questo tipo di valutazioni
nel suo libro ``Scienza e ipotesi''
dal quale sono state tratte anche le
altre citazioni. Racconta infatti delle molte soluzioni al problema della
quadratura del cerchio sottoposte all'Accademia di Francia da sconosciuti
e che venivano cestinate senza che neanche si perdesse tempo a
vagliarle.
Questo comportamento - commenta Poincaré -
deriva dall'aver soppesato
la probabilità a priori che ``ci sia un pazzo più in Francia''
con quella che uno sconosciuto potesse risolvere un problema
sul quale avevano fallito eminenti matematici.




Next: Scorciatoia al ragionamento bayesiano:
Up: Dalla probabilità degli effetti
Previous: Probabilità iniziale e probabilità
Indice
Giulio D'Agostini
2001-04-02
o dalla causa
. L'effetto è appena stato osservato. Ci domandiamo la probabilità che sia dovuto alla causa
. Questa è una probabilità di causa a posteriori. Ma non la potrei calcolare, se una convenzione più o o meno giustificata non mi dicesse in anticipo qual'è la probabilità a priori che la causa
entri in gioco''.