



Next: Riassumendo
Up: Errori e incertezze di
Previous: Rette di massima e
Indice
L'altra regola di propagazione di incertezze
generalmente nota (ma, al dire il vero, non troppo
fra gli insegnanti di scuola media)
è quella cosiddetta degli ``errori statistici'', che riportiamo
per comodità:
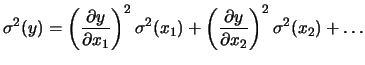 |
(11) |
Essa è decisamente meglio di quella precedente,
se non altro in quanto si sostituiscono probabilità
a incertezze.
Ma all'atto pratico anche questa formula presenta i suoi problemi.
- Innanzitutto è
da premettere il dato di fatto che
molti studenti studiano questa formula in modo astratto,
senza nessuna applicazione durante l'intero corso di laurea, e quindi
si crea un atteggiamento di diffidenza nei suoi confronti. E difatti,
alla prima occasione in cui si tenta di applicarla, nascono i problemi.
- Seconda premessa è che la
(11) non è completa, essendo valida
soltanto nel caso in cui le
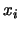 sono indipendenti,
condizione che è violata qualora le grandezze sono misurate
con lo stesso strumento, un caso tutt'altro che astratto.
sono indipendenti,
condizione che è violata qualora le grandezze sono misurate
con lo stesso strumento, un caso tutt'altro che astratto.
- Comunque, il primo problema legato
a tale formula è quello di interpretazione.
Per qualcuno potrà sembrare un cavillo filosofico, ma in realtà
è un punto cruciale. Cosa significa
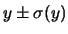 ?
La stragrande maggioranza delle persone interpellate
sono concordi nell'affermare che (assunto un modello gaussiano)
essa voglia indicare
?
La stragrande maggioranza delle persone interpellate
sono concordi nell'affermare che (assunto un modello gaussiano)
essa voglia indicare
![$\displaystyle P\left[y-\sigma(y) \le y_v \le y+\sigma(y)\right] = 68\,\%\,:$](img113.png) |
(12) |
``c'è il 68% di probabilità che il valor vero di 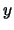 si trova
nell'intervallo
si trova
nell'intervallo
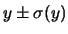 ''.
''.
Quando poi si chiede cosa sia la probabilità si ottengono
risposte tipiche (``casi favorevoli su casi possibili'' e ``limite
della frequenza'') che non contemplano affermazioni probabilistiche
sui valori veri, così come sono espresse dalla
(12).
- Un problema pratico tipico è quello
di ``cosa mettere nelle
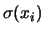 ''
della (11).
Siccome questa formula deriva dal calcolo delle probabilità,
applicato alle variabili casuali, le
''
della (11).
Siccome questa formula deriva dal calcolo delle probabilità,
applicato alle variabili casuali, le 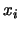 e la
e la 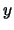 che entrano nella
formula devono avere il significato di variabile
casuale e le
che entrano nella
formula devono avere il significato di variabile
casuale e le
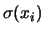 quello di deviazione standard.
Quindi, se non si associano variabili casuali ai valori veri,
l'uso della (11) è arbitrario.
quello di deviazione standard.
Quindi, se non si associano variabili casuali ai valori veri,
l'uso della (11) è arbitrario.
- Nel caso di
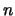 misure ripetute,
si impara che le
misure ripetute,
si impara che le
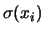 vanno calcolate come ``
vanno calcolate come ``
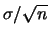 '' (nonostante
si incontra ancora qualcuno diffidente del fattore
'' (nonostante
si incontra ancora qualcuno diffidente del fattore
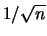 e che preferisce ometterlo per ``non avere errori troppo piccoli'').
Purtroppo, non sempre è possibile effettuare molte misure
che mostrino una variabilità da manuale dei valori letti.
Come comportarsi, ad esempio, se:
e che preferisce ometterlo per ``non avere errori troppo piccoli'').
Purtroppo, non sempre è possibile effettuare molte misure
che mostrino una variabilità da manuale dei valori letti.
Come comportarsi, ad esempio, se:
- si effettua una sola misura (
 )?
)?
- si legge un grandissimo numero di
volte (``
 '') lo stesso valore
(ad esempio 3.512 V su uno strumento digitale)?
'') lo stesso valore
(ad esempio 3.512 V su uno strumento digitale)?
- Come comportarsi se sono presenti anche ``errori sistematici''?
- Come valutare e gestire le correlazioni fra diverse misure
introdotte, ad esempio, da errori sistematici comuni?
La conseguenza di questi problemi tecnici (usualmente
quello di principio sull'interpretazione della probabilità
non viene nemmeno preso in considerazione) è che
in genere gli studenti imparano delle formule che
poi non utilizzeranno e seguitano a lavorare con
gli errori
massimi13.




Next: Riassumendo
Up: Errori e incertezze di
Previous: Rette di massima e
Indice
Giulio D'Agostini
2001-04-02
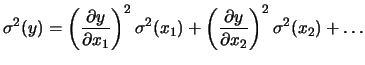
si trova nell'intervallo
''.