



Next: Probabilità iniziale e probabilità
Up: Dalla probabilità degli effetti
Previous: Dalla probabilità degli effetti
Indice
Cominciamo con la distribuzione di
probabilità dei valori osservabili,
indicati con 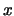 .
Come detto,
sta per la funzione densità di probabilità
(
.
Come detto,
sta per la funzione densità di probabilità
(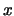 è una variabile continua, dal punto di vista pratico)
di osservare23 un
certo valore
è una variabile continua, dal punto di vista pratico)
di osservare23 un
certo valore 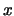 , dato un determinato valore vero
, dato un determinato valore vero 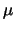 .
Tutti i possibili valori di
.
Tutti i possibili valori di 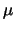 possono essere visti come le
infinite cause responsabili del valore
possono essere visti come le
infinite cause responsabili del valore 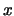 osservato
(il loro effetto). La figura 7
dovrebbe aiutare ad illustrare il problema.
osservato
(il loro effetto). La figura 7
dovrebbe aiutare ad illustrare il problema.
Figura 7:
Relazioni cause-effetti viste in termini di condizionanti
e eventi condizionati
 |
La funzione
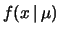 ci dà
la verosimiglianza che
ci dà
la verosimiglianza che 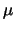 possa causare
possa causare
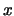 e per questo è chiamata semplicemente
verosimiglianza. Essa va stimata dalla
conoscenza del comportamento dello strumento e, più in generale,
dell'insieme di tutte le procedure di misura. Molto spesso si utilizza per
la verosimiglianza
un modello gaussiano, giustificato un po' dall'esperienza e
soprattutto dalle aspettative teoriche, basate sul teorema
del limite centrale. Consideriamo, quindi nel seguito,
per semplicità, una verosimiglianza
del tipo
e per questo è chiamata semplicemente
verosimiglianza. Essa va stimata dalla
conoscenza del comportamento dello strumento e, più in generale,
dell'insieme di tutte le procedure di misura. Molto spesso si utilizza per
la verosimiglianza
un modello gaussiano, giustificato un po' dall'esperienza e
soprattutto dalle aspettative teoriche, basate sul teorema
del limite centrale. Consideriamo, quindi nel seguito,
per semplicità, una verosimiglianza
del tipo
![$\displaystyle f(x\,\vert\,\mu) =\frac{1}{\sqrt{2\pi}\sigma} \exp{\left[-\frac{(x-\mu)^2}{2\sigma^2}\right]}$](img153.png) |
(15) |
con 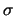 che non dipende dal valore di
che non dipende dal valore di 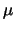 (stiamo assumendo che lo strumento
risponda nello stesso modo a tutti i possibili valori di
(stiamo assumendo che lo strumento
risponda nello stesso modo a tutti i possibili valori di 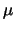 ).
).




Next: Probabilità iniziale e probabilità
Up: Dalla probabilità degli effetti
Previous: Dalla probabilità degli effetti
Indice
Giulio D'Agostini
2001-04-02