(La risposta naïve per la differenza sarebbe
Chiaramente, l'incertezza su ciascuno dei punti è 0.007V (V) ma l'errore di calibrazione non può influenzare la differenza fra valori così vicini, specialmente se è stato verificato che, alternando le letture, effettivamente i valori si ripetono. Nella differenza conta allora soltanto l'incertezza di digitalizzazione:
(La risposta naïve sarebbemV. L'incertezza di
mV è data da
.)
Per ciascuno spessore l'incertezza totale è data dalla combinazione in quadratura dell'incertezza di tipo A () e quella di tipo
(
m
). Nelle differenze bisogna tener conto delle eventuali correlazioni. Il tipo di strumento e di misura in oggetto appartengono al caso non ``facilmente schematizzabile'' discusso nel paragrafo 18.5. Ragionevoli conclusioni sono:
I gradi di fiducia sui possibili valori di temperatura possono essere modellizzati con una triangolare o con una gaussiana a 2-3 sigma. Si ha, rispettivamente, nei tre casi:C,
C e
C. Prendendo il valore intermedio si ottiene:
Applichiamo ora la correzione per la temperatura, ricordando che
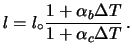
Invertendo e trascurando i termini di ordine superiore a(essendo i coefficienti
molto piccoli):
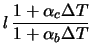 |
|||
Il volumevale
m
e la massa apparente
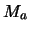
kg, da cui:
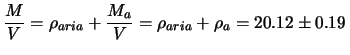 kg m kg m |
Facciamo il seguente caso (sta per umidità relativa):
Per fare i conti utilizziamo seguente formula:
doveè il valore della densità dell'aria secca, dipendente da temperatura e pressione, e
è un coefficiente che dipende soltanto dalla temperatura (vedi tabella 2).
Eseguendo le derivate per via numerica (vedi paragrafo 18.7) troviamo i seguenti contributi all'incertezza totale
Si vede quindi come il contributo più importante sia dovuto all'incertezza sulla pressione. Il valore della densità dell'aria con questo stato di conoscenza dei fattori di influenza vale quindi
Affermare chekg m
sia esatto vuol dire che il solo errore possibile è quello di arrotondamento. Quindi
kg m
. Se le quattro incertezze contribuiscono allo stesso modo, ciascuna di esse deve valere al più
kg m
Ne seguono i seguenti requisiti:
condizioni di lavoro tutt'altro che banali! Si capisce allora come, nei casi pratici, non abbia molto senso far riferimento ad una densità dell'aria con più di tre cifre significative.