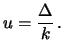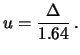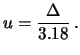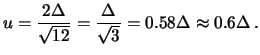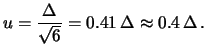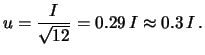Next: Esempi numerici
Up: Errori e incertezze di
Previous: Raccomandazioni BIPM/ISO
Indice
Valutazione delle incertezze di tipo B
Le incertezze di tipo 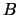 sono indubbiamente
quelle più critiche da valutare. Vediamo innanzitutto
cosa raccomanda la Guida, poi mostriamo degli esempi.
sono indubbiamente
quelle più critiche da valutare. Vediamo innanzitutto
cosa raccomanda la Guida, poi mostriamo degli esempi.
For estimate 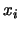 of an input quantity36
of an input quantity36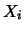 that has not been
obtained from repeated observations, the
that has not been
obtained from repeated observations, the  standard
uncertainty
standard
uncertainty 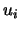 is evaluated by scientific judgement based on all the
available information on the possible variability of
is evaluated by scientific judgement based on all the
available information on the possible variability of 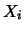 . The pool
of information may include
. The pool
of information may include
- previous measurement data;
- experience with or general knowledge of the behaviour and properties of
relevant materials and instruments;
- manufacturer's specifications;
- data provided in calibration and other certificates;
- uncertainties assigned to reference data taken from handbooks.
Detto nel linguaggio probabilistico adottato,
si cerca di modellizzare,
in base alla migliore conoscenza del problema,
la distribuzione dei gradi di fiducia
(considerando, ad esempio, gli estremi dell'intervallo
di valori possibili, se ci sono valori più credibili di altri,
e così via) e successivamente
se ne ricava la deviazione standard. Anche se la modellizzazione
è rozza e la deviazione standard che ne deriva è incerta,
è importante notare che:
- le deviazioni standard valutate da piccoli campioni di dati sperimentali
non sono meno incerte di quelle
ottenute ``by scientific judgement'';
ad esempio in un modello gaussiano l'incertezza
relativa sulla valutazione è approssimativamente uguale a
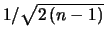 . Per
. Per 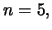 10 e 20 essa è
10 e 20 essa è
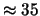 ,
24 e 16 %;
,
24 e 16 %;
- è preferibile dare le stime più verosimili delle deviazioni
standard, invece di sovrastimare per motivi di prudenza:
se si danno sempre le migliori stime, le
incertezze globali saranno mediamente corrette;
se si sovrastima ad ogni passo,
saranno mediamente esagerate anche le incertezze globali.
- il modello finale di distribuzione del valore vero
è reso circa normale dalla combinazione delle varianze
(teorema del limite centrale) indipendentemente dalla
forma esatta della distribuzione assunta.
Facciamo degli esempi.
- Misure di
altre grandezze particolari,
prossime a quella di interesse
ed eseguite nelle stesse condizioni, hanno fornito
una deviazione standard di ripetitività
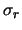 .
E' ragionevole assumere per l'incertezza
.
E' ragionevole assumere per l'incertezza
- Il certificato di calibrazione di un costruttore dichiara che
l'incertezza, definita come
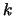 deviazioni standard,
è ``
deviazioni standard,
è ``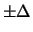 '':
'':
- Un ricercatore afferma che una certa grandezza vale,
al 90%,
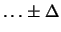 . Assumendo, ragionevolmente,
un modello gaussiano:
. Assumendo, ragionevolmente,
un modello gaussiano:
- Una pubblicazione riporta un risultato come
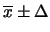 , specificando che
la media è stata eseguita con 4 valori (3 gradi di libertà)
e che l'incertezza è data al 95%. Si deduce
che, verosimilmente, l'intervallo è stato calcolato mediante
la
, specificando che
la media è stata eseguita con 4 valori (3 gradi di libertà)
e che l'incertezza è data al 95%. Si deduce
che, verosimilmente, l'intervallo è stato calcolato mediante
la 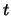 di Student. Ne segue (consultando opportune tabelle):
di Student. Ne segue (consultando opportune tabelle):
- Un manuale di istruzione dichiara che l'errore massimo che
lo strumento fornisce è compreso entro
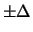 .
In mancanza di ulteriori affermazioni, si può assumere
una distribuzione uniforme:
.
In mancanza di ulteriori affermazioni, si può assumere
una distribuzione uniforme:
- Un parametro è compreso, con la quasi sicurezza, entro
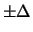 , ma si tende a credere più ai valori centrali
che a quelli estremi. In questo caso, è più ragionevole ipotizzare
una distribuzione triangolare:
In modo alternativo, l'informazione potrebbe essere anche compatibile
con un modello gaussiano con l'intervallo
a 2 o 3
, ma si tende a credere più ai valori centrali
che a quelli estremi. In questo caso, è più ragionevole ipotizzare
una distribuzione triangolare:
In modo alternativo, l'informazione potrebbe essere anche compatibile
con un modello gaussiano con l'intervallo
a 2 o 3 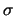 . Si otterebbero allora
. Si otterebbero allora
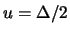 o
o 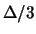 ,
valori a cavallo di quanto ottenuto con la triangolare.
Quindi quest'ultima può essere considerata un compromesso
per quantificare quello stato di incertezza.
,
valori a cavallo di quanto ottenuto con la triangolare.
Quindi quest'ultima può essere considerata un compromesso
per quantificare quello stato di incertezza.
- Si legge un valore su uno
strumento digitale, in cui l'intervallo
di scala (la variazione della grandezza associata alla
variazione di una unità della cifra meno significativa)
vale
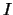 . Il valore vero potrebbe essere ovunque nell'intervallo
ampio
. Il valore vero potrebbe essere ovunque nell'intervallo
ampio 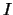 . Quindi L'incertezza da associare alla quantizzazione
della lettura è pari a
. Quindi L'incertezza da associare alla quantizzazione
della lettura è pari a




Next: Esempi numerici
Up: Errori e incertezze di
Previous: Raccomandazioni BIPM/ISO
Indice
Giulio D'Agostini
2001-04-02
of an input quantity36
that has not been obtained from repeated observations, the
standard uncertainty
is evaluated by scientific judgement based on all the available information on the possible variability of
. The pool of information may include