



Next: Errore di scala
Up: Imperfetta conoscenza delle costanti
Previous: Imperfetta conoscenza delle costanti
Indice
Cominciamo con il considerare uno strumento affetto
da un possibile errore di zero
(ove intendiamo una possibile costante additiva, in inglese
offset, da aggiungere ai valori letti).
Questo caso è illustrato in figura 9.a, dove
è mostrata la lettura sullo strumento (``risposta'') in funzione
del valore della grandezza (`stimolo'').
L'effetto di questo tipo di errore è che la
curva di risposta
potrebbe essere
traslata lungo le ordinata, ma di un valore incognito.
Infatti,
anche se uno strumento è stato calibrato, e quindi crediamo che il valore
più plausibile dell'offset sia 0, la non esattezza della calibrazione
ci fa ritenere che anche ``piccoli''
valori intorno a 0 siano possibili.
Assumiamo di potere descrivere i
diversi gradi di fiducia dell'offset con una
gaussiana33 centrata in 0 e
di deviazione standard 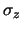 . Chiamiamo inoltre
. Chiamiamo inoltre 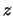 la variabile
casuale ad esso associata (
la variabile
casuale ad esso associata (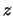 sta per ``zero vero'').
Abbiamo detto che, in assenza di errore sistematico, la grandezza
ha una incertezza
sta per ``zero vero'').
Abbiamo detto che, in assenza di errore sistematico, la grandezza
ha una incertezza
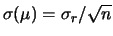 . Facciamo ora questa
trasformazione di notazione
. Facciamo ora questa
trasformazione di notazione
ovvero aggiungiamo il pedice 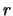 per indicare che questi sono i valori veri
ottenuti tenendo conto dei soli effetti casuali.
Per ottenere il valore che tenga conto anche della non perfetta
calibrazione bisogna sottrarre a
per indicare che questi sono i valori veri
ottenuti tenendo conto dei soli effetti casuali.
Per ottenere il valore che tenga conto anche della non perfetta
calibrazione bisogna sottrarre a 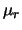 il valor vero dell'offset:
ove
il valor vero dell'offset:
ove
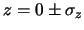 .
Dalla propagazione delle incertezze otteniamo:
.
Dalla propagazione delle incertezze otteniamo:
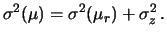 |
(26) |
L'incertezza standard
globale è quindi ottenuta combinando in
quadratura l'incertezza standard dovuta ai soli effetti casuali con
quella dell'offset.
Quando si hanno più grandezze misurate con lo stesso strumento
si applica la stessa procedura a tutte le grandezze:
Sorge ora il problema che
tutte le incertezze sono
correlate: se il valore vero dello zero dovesse valere
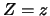 tutte le misure sarebbero sbagliate di questo valore.
Per studiare l'effetto delle
correlazioni, immaginiamo due grandezze,
tutte le misure sarebbero sbagliate di questo valore.
Per studiare l'effetto delle
correlazioni, immaginiamo due grandezze, 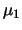 e
e 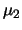 e facciamone la differenza e la somma:
e facciamone la differenza e la somma:
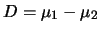 ,
,
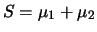 .
Applicando la propagazione delle incertezze che abbiamo
visto, sembrerebbe che
.
Applicando la propagazione delle incertezze che abbiamo
visto, sembrerebbe che
Ma c'è qualcosa che non convince; infatti, intuitivamente ci si
aspetta che una incertezza dovuta all'offset debba essere ininfluente
sulle differenze: un termometro può anche essere
scalibrato di 10 C, ma questo non può influenzare una
misura di differenza di temperature.
Riscriviamo allora i valori veri a partire
da quelli ``solo random'' più l'effetto dell'offset:
C, ma questo non può influenzare una
misura di differenza di temperature.
Riscriviamo allora i valori veri a partire
da quelli ``solo random'' più l'effetto dell'offset:
Ne segue quindi
ben diverse da quelle precedenti e molto più ragionevoli.




Next: Errore di scala
Up: Imperfetta conoscenza delle costanti
Previous: Imperfetta conoscenza delle costanti
Indice
Giulio D'Agostini
2001-04-02
![]() . Chiamiamo inoltre
. Chiamiamo inoltre ![]() la variabile
casuale ad esso associata (
la variabile
casuale ad esso associata (![]() sta per ``zero vero'').
Abbiamo detto che, in assenza di errore sistematico, la grandezza
ha una incertezza
sta per ``zero vero'').
Abbiamo detto che, in assenza di errore sistematico, la grandezza
ha una incertezza
![]() . Facciamo ora questa
trasformazione di notazione
. Facciamo ora questa
trasformazione di notazione