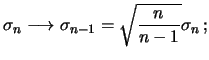Next: Singole misure di grandezze
Up: Caso di ignota
Previous: Caso di ignota
Indice
Misure ripetute della stessa grandezza fisica
Questo caso si riconduce a quello di 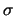 nota quando il
numero
di misure è abbastanza grande:
nota quando il
numero
di misure è abbastanza grande:
- il valore vero è in prossimità della media aritmetica,
con una incertezza che decresce come
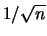 ;
;
- la deviazione standard dell'errore statistico (``valore osservato
meno valore vero'') può essere stimato dalla deviazione
standard degli scarti dei singoli
valori osservati rispetto alla media29:
con
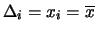 .
.
Quando invece 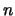 è piccolo
(al di sotto della decina, tipicamente),
nascono altre complicazioni, in quanto:
è piccolo
(al di sotto della decina, tipicamente),
nascono altre complicazioni, in quanto:
- innanzitutto
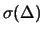 non è una buona stima di
non è una buona stima di 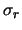 (si pensi al caso limite di
(si pensi al caso limite di  );
);
- in secondo luogo, la verosimiglianza dipende dal parametro ignoto
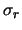 sul quale c'è stato di incertezza: la banale inversione di probabilità
tipo cane-cacciatore non è più ovvia.
sul quale c'è stato di incertezza: la banale inversione di probabilità
tipo cane-cacciatore non è più ovvia.
Come si può intuire, il problema diventa complicato.
La soluzione usuale della statistica convenzionale consiste in
- aumentare la deviazione standard stimata per tenere conto
che la media è legata (``vincolata'') ai valori stessi e che quindi
la deviazione standard
tende ad essere sottostimata rispetto a quanto si otterrebbe
disponendo di un campione più numeroso (si pensi al caso limite
 );
si preferisce allora usare
);
si preferisce allora usare
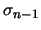
- cambiare il tipo di distribuzione finale: dalla gaussiana alla
cosiddetta
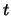 di Student.
di Student.
In realtà, anche se questi metodi vanno in qualche modo
``nella direzione'' giusta,
bisogna fare attenzione a non prenderli troppo alla lettera.
Ad esempio, se si osservano due valori che differiscono di 0.3 mm
e si applica ciecamente questo metodo ne risulta
un intervallo di
incertezza di quasi 10 cm qualora si richiedesse un ``livello di confidenza''
del 99.9%. Qualsiasi meccanico troverebbe ridicola questa conclusione.
Molto spesso,
quando 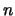 è veramente dell'ordine dell'unità, può essere
più sensato quello che si sapeva su
è veramente dell'ordine dell'unità, può essere
più sensato quello che si sapeva su 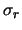 prima della misura di quanto si possa ricavare
dai dati stessi (su questo punto ritorneremo fra breve).
Quando invece il problema è veramente
critico è essenziale ripetere più volte le misure. Quando infine
prima della misura di quanto si possa ricavare
dai dati stessi (su questo punto ritorneremo fra breve).
Quando invece il problema è veramente
critico è essenziale ripetere più volte le misure. Quando infine
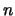 è già dell'``ordine di 10'' (ma anche 5-6
può andare abbastanza bene), l'inversione gaussiana diventa
abbastanza ragionevole.
è già dell'``ordine di 10'' (ma anche 5-6
può andare abbastanza bene), l'inversione gaussiana diventa
abbastanza ragionevole.




Next: Singole misure di grandezze
Up: Caso di ignota
Previous: Caso di ignota
Indice
Giulio D'Agostini
2001-04-02