



Next: Probabilità soggettiva
Up: Errori e incertezze di
Previous: Riassumendo
Indice
Per ricostruire una teoria delle incertezza di misura che non soffra
di tutte i problemi mostrati, partiamo da alcune considerazioni.
- Un po' in analogia del ``cogito'' cartesiano, a questo punto,
l'unica affermazione sulla quale è difficile non
essere d'accordo è quanto detto nell'introduzione:
il processo di induzione
dalle osservazioni ai valori di grandezze fisiche
conduce ad affermazioni che, inevitabilmente,
sono affette da un certo grado di incertezza.
- Il concetto naturale sviluppato dalla
mente umana per quantificare
la plausibilità delle affermazioni in
situazioni di incertezza è quello di
proba-bilità.
Si tratta quindi di costruire una teoria probabilistica
(probabilistica e non, genericamente, ``statistica'')
dell'incertezza di misura.
Questi due punti di partenza sembrano assolutamente ragionevoli,
ma il secondo appare in contraddizione con la critica sull'interpretazione
probabilistica del risultato, avanzata nel paragrafo precedente.
In realtà questo non è un vero problema,
ma soltanto un prodotto di una visione distorta
(cioè diversa da quella naturale) del concetto di probabilità.
In effetti la maggior parte dei fisici stessi,
pur ``credendo'' che la probabilità sia
``il rapporto fra casi favorevoli e casi contrari'' o
``limite della frequenza''17,
si stupiscono quando vengono a sapere che
l'affermazione
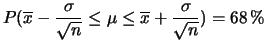 |
(13) |
è illegittima18 (indichiamo con 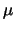 il valore vero
e con
il valore vero
e con 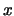 il valore osservato). Infatti, secondo la
statistica convenzionale, non hanno senso affermazioni
probabilistiche sul valor vero.
Esso sarebbe
un valore ``costante, ma ignoto''. In tale approccio si può
affermare soltanto che
il valore osservato). Infatti, secondo la
statistica convenzionale, non hanno senso affermazioni
probabilistiche sul valor vero.
Esso sarebbe
un valore ``costante, ma ignoto''. In tale approccio si può
affermare soltanto che
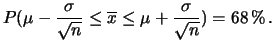 |
(14) |
Ma questa è un'affermazione probabilistica
su
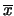 , dati
, dati 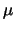 e
e 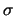 .
Non sono ammesse invece affermazioni probabilistiche su
.
Non sono ammesse invece affermazioni probabilistiche su 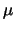 ,
sebbene sia a queste che lo sperimenatore faccia
riferimento quando esegue un esperimento
per ``diminuire lo stato di incertezza su
,
sebbene sia a queste che lo sperimenatore faccia
riferimento quando esegue un esperimento
per ``diminuire lo stato di incertezza su 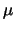 ''.
''.




Next: Probabilità soggettiva
Up: Errori e incertezze di
Previous: Riassumendo
Indice
Giulio D'Agostini
2001-04-02