| (1.7) |
Per quanto riguarda invece la dipendenza della risposta dallo
stimolo, essa è data dalla caratteristica di trasferimento
(o di risposta), esprimibile mediante una relazione
matematica, una tabella numerica o un grafico (vedi
figura ![]() ).
).
Il rapporto fra il cambiamento di risposta diviso il corrispondente cambiamento dello stimolo (sufficientemente piccolo) definisce la sensibilità dello strumento. Dal punto di vista matematico la risposta è legata alla derivata della curva caratteristica di risposta:
Sensibilità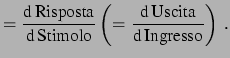 |
(1.8) |
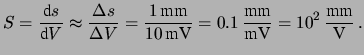 |
(1.9) |
Nei tratti in cui
la sensibilità è costante l'andamento della curva di risposta
è lineare
(vedi figura ![]() ).
Negli strumenti con scala lineare la sensibilità è pari al
rapporto fra la spaziatura
della scala (espressa in mm)
e l'intervallo di
scala (espresso in unità di misura della grandezza
fisica). Ad esempio consideriamo
un termometro clinico
a mercurio la cui colonnina si alza di 10 cm (la lunghezza di scala)
quando l'indicazione
varia fra la temperatura minima di 35 e e la
massima di
42
).
Negli strumenti con scala lineare la sensibilità è pari al
rapporto fra la spaziatura
della scala (espressa in mm)
e l'intervallo di
scala (espresso in unità di misura della grandezza
fisica). Ad esempio consideriamo
un termometro clinico
a mercurio la cui colonnina si alza di 10 cm (la lunghezza di scala)
quando l'indicazione
varia fra la temperatura minima di 35 e e la
massima di
42 ![]() C (estensione di scala di
7
C (estensione di scala di
7 ![]() C). Poiché la curva di risposta è lineare,
la sensibilità del termometro è di 1.43 cm/
C). Poiché la curva di risposta è lineare,
la sensibilità del termometro è di 1.43 cm/![]() C.
C.
Non sempre una variazione dello stimolo si ripercuote in una variazione della risposta. A volte, ad esempio a causa di attriti, l'ingresso può variare senza produrre variazioni della risposta. Si definisce allora soglia di discriminazione la più grande variazione di segnale di ingresso che non provoca variazione percepibile della risposta, a condizione che la variazione sia lenta e monotòna. Quando invece si considera l'intervallo massimo all'interno del quale si può far variare il segnale di ingresso nei due sensi senza provocare variazione della risposta si parla di zona morta. A volte si aumenta volontariamente la zona morta per evitare la variazione di risposta dovuta a piccole variazioni dell'ingresso. Un buon esempio, anche se non direttamente legato alle misure, è quello del volante di un'auto. Lo stimolo è la rotazione del volante. La risposta è il cambiamento di direzione delle ruote. Per evitare variazioni continue di direzione dovuto a piccoli movimenti delle mani viene appositamente progettata una zona morta tale che una piccola rotazione iniziale del volante non provoca alcun cambiamento di direzione delle ruote.
A volte invece non si osserva una variazione della risposta
dello strumento, anche se essa può essersi verificata, in quanto
non percepibile. La caratteristica dello strumento
legata a questa eventualità è la risoluzione.
Essa è definita come
la più piccola differenza di indicazione di un dispositivo
che può essere percepito in maniera significativa.
Mentre nel caso di scale digitali la risoluzione è uguale
all'incremento digitale, nel caso di scale analogiche essa dipende
dall'osservatore, dalla spaziatura della scala e dalle condizioni
di lavoro
ed è generalmente
dell'ordine ``dei decimi'' di intervallo di scala (ovvero
della variazione di valore corrispondente ad una divisione).
Ad esempio viene comunemente accettato che uno sperimentatore
possa risolvere la posizione di una divisione con una risoluzione
di 1/5 di divisione, ovvero che egli possa decidere con la ``quasi certezza''
se l'ago è all'interno di un intervallino di larghezza 0.2 divisioni.
È quindi raccomandabile di provare a stimare i decimi e di dare
successivamente alla lettura un'incertezza che dipende dalla
propria capacità di stima (vedi ![]() ).
).
È da notare inoltre l'uso pecululiare del termine risoluzione, analogo a quello di precisione: minore è la grandezza che si riesce a risolvere, maggiore è la risoluzione dello strumento. Ad esempio, un microscopio elettronico ha una risoluzione molto maggiore di un microscopio ottico.