Next: Un esempio storico di
Up: Previsione di una distribuzione
Previous: Previsione di una distribuzione
Indice
Terminiamo con una breve introduzione su un argomento che
tratteremo più in dettaglio nel
capitolo ***correlazione***.
Fare una previsione di una distribuzione statistica
comporta inevitabilmente una trattazione
simultanea di molte variabili casuali (le  dell'esempio
precedente). Abbiamo visto come la valutazione di ciascuno
dei valori attesi non richieda nuovi concetti. Si presenta invece
un problema nuovo quando vogliamo fare una previsione globale
della distribuzione.
Ad esempio, mentre riteniamo ragionevole
che la variabile
dell'esempio
precedente). Abbiamo visto come la valutazione di ciascuno
dei valori attesi non richieda nuovi concetti. Si presenta invece
un problema nuovo quando vogliamo fare una previsione globale
della distribuzione.
Ad esempio, mentre riteniamo ragionevole
che la variabile  cada fra
E
cada fra
E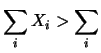 e
e 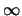 ,
è impossibile che ciascuna delle variabili
sia compresa in quell'intervallo, in quanto implicherebbe
che
,
è impossibile che ciascuna delle variabili
sia compresa in quell'intervallo, in quanto implicherebbe
che
cosa impossibile in quanto la somma di ciascuna delle possibili
frequenze deve essere uguale al numero totale di esperimenti.
Ciò significa che
alcune di queste possono essere valori maggiori delle loro
previsioni se sono compensate da altre che assumono valori inferiori.
Si dice che queste variabili casuali sono correlate
(per ora nel senso che questo termine può significare
nel linguaggio comune).
Un caso estremo è quando si hanno soltanto
due variabili, ad esempio gli esperimenti precedentemente
descritti consistano nel
lancio di una sola moneta (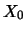 ).
). 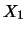 sarà il numero di teste e
sarà il numero di teste e
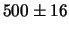 il numero di croci. Su
il numero di croci. Su 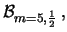 esperimenti ci
aspettiamo
esperimenti ci
aspettiamo 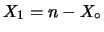 teste e
teste e 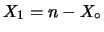 croci,
ma la loro somma non è un numero aleatorio
(deve dare con certezza 1000)
e quindi
le due variabili sono linearmente dipendenti (
croci,
ma la loro somma non è un numero aleatorio
(deve dare con certezza 1000)
e quindi
le due variabili sono linearmente dipendenti (
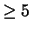 )
e completamente anticorrelate.
)
e completamente anticorrelate.




Next: Un esempio storico di
Up: Previsione di una distribuzione
Previous: Previsione di una distribuzione
Indice
Giulio D'Agostini
2001-04-02
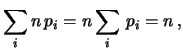
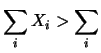 e
e