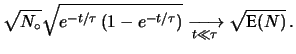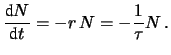Next: Assenza di memoria di
Up: Processo di Poisson -
Previous: Tempo di attesa del
Indice
Supponiamo di avere un nucleo radioattivo (o una particella
subnucleare instabile) per il quale
la probabilità di decadimento sia indipendente dal tempo,
ovvero 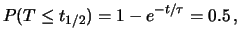 . Per quanto detto a proposito del
processo di Poisson, l'istante di decadimento del nucleo
a partire da un certo istante scelto arbitrariamente
è descritto da una distribuzione esponenziale di
parametro
. Per quanto detto a proposito del
processo di Poisson, l'istante di decadimento del nucleo
a partire da un certo istante scelto arbitrariamente
è descritto da una distribuzione esponenziale di
parametro  . Il valore atteso del tempo di decadimento è
pari a
. Il valore atteso del tempo di decadimento è
pari a 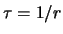 , chiamato anche vita media di decadimento.
È interessante calcolare il tempo tale che ci sia il 50%
di probabilità che la particella sia già decaduta
(ovvero la mediana della
distribuzione):
ovvero
La mediana è chiamata, in questa applicazione, anche
tempo di dimezzamento.
Per capire meglio il suo significato, consideriamo
, chiamato anche vita media di decadimento.
È interessante calcolare il tempo tale che ci sia il 50%
di probabilità che la particella sia già decaduta
(ovvero la mediana della
distribuzione):
ovvero
La mediana è chiamata, in questa applicazione, anche
tempo di dimezzamento.
Per capire meglio il suo significato, consideriamo
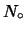 nuclei all'istante
nuclei all'istante 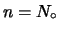 , inizio delle nostre
osservazioni, e calcoliamoci previsione e incertezza di previsione
del numero di nuclei che sono rimasti non decaduti all'istante
, inizio delle nostre
osservazioni, e calcoliamoci previsione e incertezza di previsione
del numero di nuclei che sono rimasti non decaduti all'istante  .
Dobbiamo considerare una distribuzione binomiale
avente
.
Dobbiamo considerare una distribuzione binomiale
avente 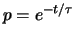 e
e
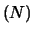 e, quindi,
di valore atteso e deviazione standard
e, quindi,
di valore atteso e deviazione standard
Dopo un tempo 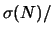 il numero iniziale di nuclei si è
dimezzato. Si noti inoltre come, per
il numero iniziale di nuclei si è
dimezzato. Si noti inoltre come, per 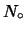 molto grandi
(tipicamente si considerano numeri dell'ordine di
grandezza del numero di Avogadro)
molto grandi
(tipicamente si considerano numeri dell'ordine di
grandezza del numero di Avogadro)
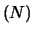 E
E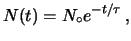 è
molto minore di 1 anche per
è
molto minore di 1 anche per  abbastanza maggiore della vita media.
Quindi la previsione del numero di nuclei non decaduti
può essere considerata con ottima approssimazione
una predizione deterministica che obbedisce ad una legge del tipo
soluzione dell'equazione differenziale
Essa può essere espressa dicendo che ``il numero di decadimenti
nell'unità di tempo è proporzionale al numero di nuclei,
con un fattore di proporzionalità pari all'inverso della vita media di
decadimento''.
abbastanza maggiore della vita media.
Quindi la previsione del numero di nuclei non decaduti
può essere considerata con ottima approssimazione
una predizione deterministica che obbedisce ad una legge del tipo
soluzione dell'equazione differenziale
Essa può essere espressa dicendo che ``il numero di decadimenti
nell'unità di tempo è proporzionale al numero di nuclei,
con un fattore di proporzionalità pari all'inverso della vita media di
decadimento''.




Next: Assenza di memoria di
Up: Processo di Poisson -
Previous: Tempo di attesa del
Indice
Giulio D'Agostini
2001-04-02