



Next: Ricapitolando
Up: Altre distribuzioni di interesse
Previous: di Student
Indice
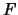
La distribuzione di Fisher (o di Fisher-Snedecor) chiamata anche
semplicemente 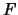 è data da
è data da
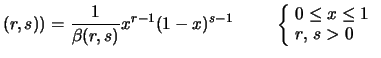 F F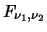 |
(8.50) |
Talvolta la variabile che segue la distribuzione 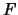 è indicata anch'essa con il simbolo
è indicata anch'essa con il simbolo
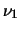 .
I parametri
.
I parametri 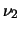 e
e 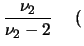 , non necessariamente intero è detti
numeri di gradi di libertà.
Valore atteso e varianza sono:
, non necessariamente intero è detti
numeri di gradi di libertà.
Valore atteso e varianza sono:
E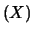 |
 |
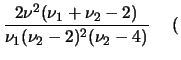 se se  |
(8.51) |
Var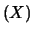 |
 |
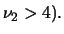 se se 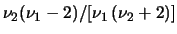 |
(8.52) |
La moda vale
![$ \nu_2(\nu_1-2)/[\nu_1\,(\nu_2+2)]$](img2116.png) se
se 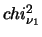 , altrimenti
essa vale 0.
, altrimenti
essa vale 0.
La proprietà che rende interessante la distribuzione di Fisher
è la seguente: se due variabili
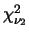 e
e
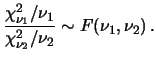 sono indipendenti, allora il
rapporto fra le due variabili, ciascuna divisa per il proprio numero
di gradi di libertà, è distribuita secondo una
sono indipendenti, allora il
rapporto fra le due variabili, ciascuna divisa per il proprio numero
di gradi di libertà, è distribuita secondo una 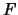 :
:
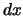 |
(8.53) |




Next: Ricapitolando
Up: Altre distribuzioni di interesse
Previous: di Student
Indice
Giulio D'Agostini
2001-04-02
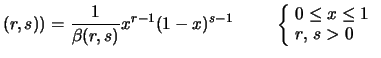 F
F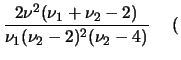 se
se 
![]() e
e
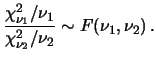 sono indipendenti, allora il
rapporto fra le due variabili, ciascuna divisa per il proprio numero
di gradi di libertà, è distribuita secondo una
sono indipendenti, allora il
rapporto fra le due variabili, ciascuna divisa per il proprio numero
di gradi di libertà, è distribuita secondo una ![]() :
: