Next: varie
Up: Variabili casuali multiple
Previous: Derivate di rispetto alle
Indice
Il concetto di distribuzione multivariata si estende anche
al caso delle distribuzioni statistiche, prestando attenzione
a tenere ben divisi i concetti, che per comodità ripetiamo:
nella distribuzione di probabilità si associa un grado di
fiducia ad ogni
vettore che descrive un possibile esito; nel caso di
distribuzione statistica si associa ad esso un peso statistico
dato dalla frequenza relativa con cui i vettori di esiti si sono
verificati. Nel caso discreto le due distribuzioni
sono quindi formalmente equivalente:
| variabili casuali: |
|
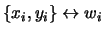 |
|
| variabili statistiche: |
|
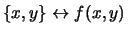 |
|
Nel caso di distribuzioni statistiche non ha molto senso parlare
di variabili continue, in quanto i numeri che si registrano
hanno sempre una risoluzione finita. Ne segue che gli analoghi degli
elementi infinitesimi di probabilità sono i pesi statistici
di una celletta di dimensione finita:
| variabili casuali: |
|
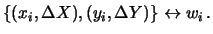 d d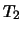 d d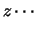 |
|
| variabili statistiche: |
|
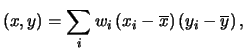 |
|
Anche nel caso di distribuzioni statistiche si può
fare uso di covarianza e deviazione standard per riassumere
la correlazione fra variabili statistiche, tenendo conto
delle solite note sulle diversità di interpretazione delle
grandezze di nome analogo.
Se abbiamo  coppie di valori, ciascuna di peso statistico
coppie di valori, ciascuna di peso statistico 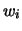 ,
abbiamo
,
abbiamo
Cov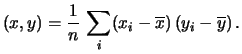 |
(9.71) |
che nel caso di pesi tutti uguali abbiamo
Cov |
(9.72) |




Next: varie
Up: Variabili casuali multiple
Previous: Derivate di rispetto alle
Indice
Giulio D'Agostini
2001-04-02
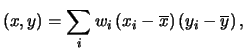
![]() coppie di valori, ciascuna di peso statistico
coppie di valori, ciascuna di peso statistico ![]() ,
abbiamo
,
abbiamo