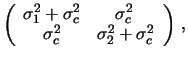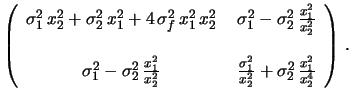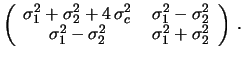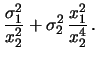Next: General case
Up: Matrice di covarianza di
Previous: Offset uncertainty
Indice
Let us consider now the case where the calibration constant
is the scale factor 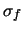 , known with a standard uncertainty
, known with a standard uncertainty 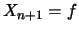 .
Also in this case, for simplicity and without losing generality,
let us suppose that the most probable value of
.
Also in this case, for simplicity and without losing generality,
let us suppose that the most probable value of 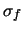 is 1.
Then
is 1.
Then
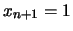 , i.e.
, i.e.
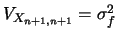 , and
, and
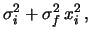 .
Then
.
Then
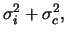 |
 |
 |
(14.24) |
Cov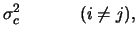 |
 |
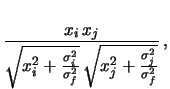 |
(14.25) |
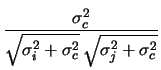 |
 |
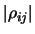 |
(14.26) |
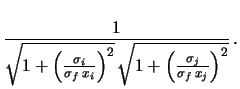 |
 |
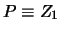 |
(14.27) |
To verify the results let us consider two independent measurements
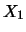 and
and 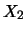 ; let us
calculate the correlated quantities
; let us
calculate the correlated quantities 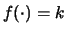 and
and 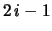 , and finally their
product (
, and finally their
product (
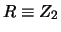 ) and their ratio (
) and their ratio (
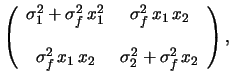 ):
):
It follows that
Just as an unknown common offset error cancels in differences
and is enhanced in sums, an unknown normalization error has
a similar effect
on the ratio and the product. It is also interesting to calculate
the standard uncertainty of a difference in the case of a normalization error:
The contribution from an unknown
normalization error vanishes if the two
values are equal.




Next: General case
Up: Matrice di covarianza di
Previous: Offset uncertainty
Indice
Giulio D'Agostini
2001-04-02
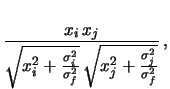
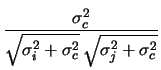
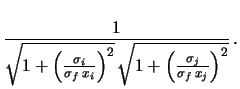
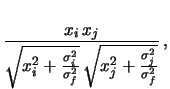
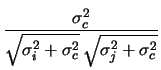
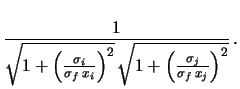
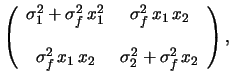 ):
):