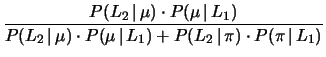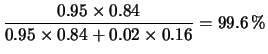Next: Statistica bayesiana: imparare dall'esperienza
Up: Esempi tipici di applicazione
Previous: Classificazione di eventi e
Indice
Per rispondere all'ultima domanda del problema precedente si può
pensare a due possibili approcci:
- calcolare le probabilità condizionate
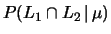 e
e
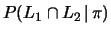 e usare il teorema di Bayes per trovare
e usare il teorema di Bayes per trovare
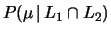 ;
;
- utilizzare la probabilità finale condizionata dall'evento
 al posto di
al posto di
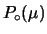 e applicare il teorema di Bayes rispetto
al secondo condizionamento di
e applicare il teorema di Bayes rispetto
al secondo condizionamento di 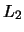 .
.
Siccome le due soluzioni sono entrambe ragionevoli e non c'è nessun
motivo per preferire una via rispetto all'altra, ci attendiamo che,
se il metodo di aggiornamento bayesiano è ragionevole, dovremmo
arrivare agli stessi risultati. In effetti questo è quanto succede.
- Seguendo il primo metodo si ha:
(Si ricordi l'ipotesi di indipendenza fra le risposte
dei due rivelatori. I conti vengono lasciati per esercizio.)
- Nel secondo caso abbiamo invece:
Si ottiene quindi lo stesso valore di probabilità finale.
Questo è un grosso pregio di questo metodo. Infatti
come è naturale pensare, le conclusioni scientifiche
possono dipendere dalle ipotesi iniziali e dalle informazioni
sperimentali, ma non devono dipendere dall'uso che si fa delle informazioni
stesse.
L'uso iterativo del teorema di Bayes può essere riassunto dicendo che
la probabilità iniziale di una inferenza è pari alla
probabilità finale dell'inferenza precedente.




Next: Statistica bayesiana: imparare dall'esperienza
Up: Esempi tipici di applicazione
Previous: Classificazione di eventi e
Indice
Giulio D'Agostini
2001-04-02