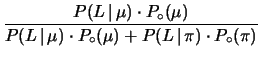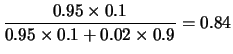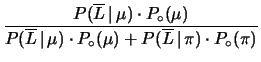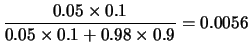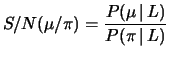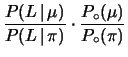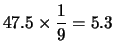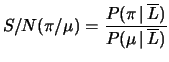Next: Uso iterativo del teorema
Up: Esempi tipici di applicazione
Previous: Esempi tipici di applicazione
Indice
Figura:
Schematizzazione in termini induttivi e deduttivi
del problema dell'identificazione di particelle con strumento
non ideale. Lo spessore delle freccie indica le direzioni
favorite dei processi di deduzione e di induzione
in questo esempio.
 |
Supponiamo che un rivelatore abbia un'efficienza
di identificazione delle particelle  del 95% e una
probabilità di confondere una particella
del 95% e una
probabilità di confondere una particella 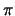 per un
per un  del 2%. Se una particella viene identificata come
del 2%. Se una particella viene identificata come  si accende
una lampadina (
si accende
una lampadina (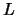 ). Conoscendo che le particelle del fascio contengono
il 10% di
). Conoscendo che le particelle del fascio contengono
il 10% di  e il 90% di
e il 90% di 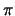 :
:
- -
- quanto vale la probabilità
che, se si accende la lampadina, sia passato un
 ?
?
- -
- quanto vale la probabilità
che, se non si accende la lampadina, sia passato un
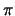 ?
?
- -
- Quanto vale il rapporto segnale rumore
(
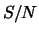 )? (Definiamo
)? (Definiamo 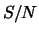 come probabilità di
come probabilità di  diviso
probabilità di
diviso
probabilità di 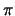 se si è accesa la lampadina, considerando
la particella
se si è accesa la lampadina, considerando
la particella  come
``segnale'', ovvero il fenomeno di interesse.)
come
``segnale'', ovvero il fenomeno di interesse.)
- -
- Come cambiano i risultati se si pongono sul fascio
due contatori aventi le stesse caratteristiche e funzionanti
indipendentemente?
Schematizziamo, con il formalismo delle probabilità condizionate,
le informazioni che abbiamo a disposizione e le domande a cui
vogliamo rispondere
(vedi figura 5.5).
-
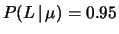
- è la probabilità che si accenda
la lampadina se l'ipotesi ``
 '' è vera, ossia se passa una vera
particella
'' è vera, ossia se passa una vera
particella  . Essa viene stimata attraverso la frequenza relativa
con la quale si accende la lampadina quando il rivelatore viene
esposto ad un fascio ``di soli
. Essa viene stimata attraverso la frequenza relativa
con la quale si accende la lampadina quando il rivelatore viene
esposto ad un fascio ``di soli  '' (ammettiamo che sia possibile).
L'uso del valore di frequenza relativa implica che
'' (ammettiamo che sia possibile).
L'uso del valore di frequenza relativa implica che
- -
- le proprietà dei
 non cambiano con il tempo (e questo
è pacifico);
non cambiano con il tempo (e questo
è pacifico);
- -
- il rivelatore e l'elettronica si comporteranno durante
l'esperimento esattamente come si erano comportati durante il test
(e questo può essere questionabile, ma assumiamo che sia vero).
-
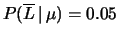
- è la probabilità dell'evento complementare;
-
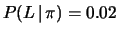
- è la probabilità
che la lampadina si accenda ``per errore'', nel senso che
assumiamo che il rivelatore sia stato progettato per identificare i
 e quindi uno strumento perfetto
darebbe5.3
e quindi uno strumento perfetto
darebbe5.3
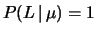 e
e
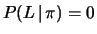 .
.
-
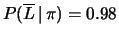
- , complementare
a
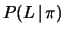 . Lo strumento ideale darebbe
. Lo strumento ideale darebbe
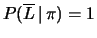 .
Anche per questo dato valgono
le note a proposito di
.
Anche per questo dato valgono
le note a proposito di
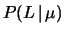 .
.
-
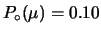
- è la probabilità iniziale
che una particella che arrivi al rivelatore sia un
 in assenza
dell'informazione che la lampadina si sia accesa o no.
in assenza
dell'informazione che la lampadina si sia accesa o no.
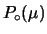 sta per
sta per
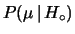 , dove
, dove 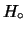 include tutta l'informazione
sulla composizione del fascio.
include tutta l'informazione
sulla composizione del fascio.
-
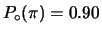 :
:
- probabilità iniziale
dell'evento
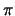 .
La somma
.
La somma
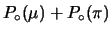 deve dare 1, in quanto gli
eventi
deve dare 1, in quanto gli
eventi  e
e 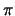 formano una classe completa di ipotesi rispetto a questo problema
e sono relativi allo stesso stato di informazione
formano una classe completa di ipotesi rispetto a questo problema
e sono relativi allo stesso stato di informazione 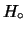 .
.
-
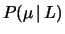 :
:
- è la probabilità che la particella
abbia attraversato il rivelatore sia un
 se la lampadina si è accesa.
La complementare ad essa sarà
se la lampadina si è accesa.
La complementare ad essa sarà
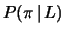 .
.
Chiaramente ci sono tutte le condizioni di applicabilità del
teorema di Bayes. Ne segue:
Siamo più sicuri che quando non si accende la luce sia passato
un 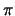 di quanto non lo siamo quando identifichiamo un
di quanto non lo siamo quando identifichiamo un  nel caso contrario. Per capirne il motivo studiamo il rapporto
segnale rumore nei due casi:
nel caso contrario. Per capirne il motivo studiamo il rapporto
segnale rumore nei due casi:
La migliore prestazione nella separazione dei 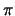 dai
dai  non è quindi dovuta alle caratteristiche del rivelatore, bensì alla
composizione del fascio.
non è quindi dovuta alle caratteristiche del rivelatore, bensì alla
composizione del fascio.
Questo ci insegna che quando le condizioni sono di alto rumore
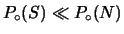 |
(5.18) |
l'esperimento deve essere molto selettivo:
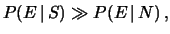 |
(5.19) |
dove 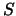 ,
, 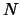 e
e  indicano genericamente segnale, rumore (inglese ``noise'')
e esito.
indicano genericamente segnale, rumore (inglese ``noise'')
e esito.




Next: Uso iterativo del teorema
Up: Esempi tipici di applicazione
Previous: Esempi tipici di applicazione
Indice
Giulio D'Agostini
2001-04-02