Where is the problem?

The question is very simple. No matter which test statistic has been used, there is no simple logical relation between a p-value and the probability of the hypothesis to test (`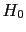$H_0$' -- in this case `` $H_0 = \mbox{No New Physics}$'').

Indeed, p-values are notoriously misunderstood, as well explained in a section of Wikipedia that I report here verbatim for the convenience of the reader[11], highlighting the sentences that mostly concern our discourse.

1. ``The p-value is not the probability that the null hypothesis is true. In fact, frequentist statistics does not, and cannot, attach probabilities to hypotheses. Comparison of Bayesian and classical approaches shows that a p-value can be very close to zero while the posterior probability of the null is very close to unity (if there is no alternative hypothesis with a large enough a priori probability and which would explain the results more easily). This is the Jeffreys-Lindley paradox.
2. The p-value is not the probability that a finding is ``merely a fluke.'' As the calculation of a p-value is based on the assumption that a finding is the product of chance alone, it patently cannot also be used to gauge the probability of that assumption being true. This is different from the real meaning which is that the p-value is the chance of obtaining such results if the null hypothesis is true.
3. The p-value is not the probability of falsely rejecting the null hypothesis. This error is a version of the so-called prosecutor's fallacy.
4. The p-value is not the probability that a replicating experiment would not yield the same conclusion.
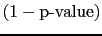5. $(1 - \mbox{p-value})$ is not the probability of the alternative hypothesis being true.
6. The significance level of the test is not determined by the p-value. The significance level of a test is a value that should be decided upon by the agent interpreting the data before the data are viewed, and is compared against the p-value or any other statistic calculated after the test has been performed. (However, reporting a p-value is more useful than simply saying that the results were or were not significant at a given level, and allows the reader to decide for himself whether to consider the results significant.)
7. The p-value does not indicate the size or importance of the observed effect (compare with effect size). The two do vary together however - the larger the effect, the smaller sample size will be required to get a significant p-value.''

Are you still sure you had really understood what p-values mean?