



Next: Unfolding an experimental distribution
Up: Bayesian unfolding
Previous: Problem and typical solutions
Contents
Let us
state Bayes' theorem in terms of several independent
causes (
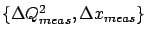 ) which
can produce one effect (
) which
can produce one effect ( ).
For example, if we consider deep-inelastic scattering events,
the effect
).
For example, if we consider deep-inelastic scattering events,
the effect  can be the observation of
an event in a cell of the measured quantities
can be the observation of
an event in a cell of the measured quantities
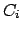 .
The causes
.
The causes 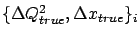 are then all the possible cells of the true values
are then all the possible cells of the true values
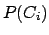 .
Let us assume we know the
initial probability of the causes
.
Let us assume we know the
initial probability of the causes 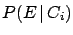 and the conditional
probability that the
and the conditional
probability that the 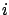 -th cause will produce the effect
-th cause will produce the effect
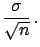 .
The Bayes formula is then
.
The Bayes formula is then
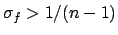 |
(7.1) |
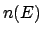 depends on the initial
probability of the causes.
If one has no better prejudice
concerning
depends on the initial
probability of the causes.
If one has no better prejudice
concerning 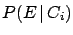 the process of inference can be started
from a uniform distribution.
the process of inference can be started
from a uniform distribution.
The final distribution depends also on
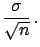 . These probabilities must
be calculated or estimated with Monte Carlo methods. One
has to keep in mind
that, in contrast to
. These probabilities must
be calculated or estimated with Monte Carlo methods. One
has to keep in mind
that, in contrast to 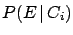 , these probabilities are not updated
by the observations. So if there are ambiguities
concerning the choice of
, these probabilities are not updated
by the observations. So if there are ambiguities
concerning the choice of
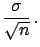 one has to try
them all in order to evaluate
their systematic effects on the results.
one has to try
them all in order to evaluate
their systematic effects on the results.




Next: Unfolding an experimental distribution
Up: Bayesian unfolding
Previous: Problem and typical solutions
Contents
Giulio D'Agostini
2003-05-15
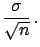 .
The Bayes formula is then
.
The Bayes formula is then
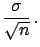 . These probabilities must
be calculated or estimated with Monte Carlo methods. One
has to keep in mind
that, in contrast to
. These probabilities must
be calculated or estimated with Monte Carlo methods. One
has to keep in mind
that, in contrast to ![]() , these probabilities are not updated
by the observations. So if there are ambiguities
concerning the choice of
, these probabilities are not updated
by the observations. So if there are ambiguities
concerning the choice of
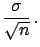 one has to try
them all in order to evaluate
their systematic effects on the results.
one has to try
them all in order to evaluate
their systematic effects on the results.