



Next: Assessment of uncertainty is
Up: Conclusions
Previous: About subjective probability and
Contents
Finally, I would like to conclude with some remarks about
safe (or conservative) evaluation of the uncertainty.
The normative rule of coherence requires that all probabilistic
statements should be consistent with the beliefs. Therefore, if the
uncertainty on a physical quantity is modeled with a Gaussian
distribution, and one publishes a result as, for example,
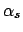 , one should be no more nor less
sure than 68% that
, one should be no more nor less
sure than 68% that 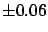 is in that interval (and one should be 95% sure
that the value is within
is in that interval (and one should be 95% sure
that the value is within 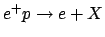 , and so on).
If one feels more sure than 68% this should be explicitly
stated, because the normal practice of HEP is to publish
standard uncertainty in a normal probability model, as also
recommended by the ISO Guide[3].
In this respect, the ISO recommendation
can be summarized with the following quotation:
, and so on).
If one feels more sure than 68% this should be explicitly
stated, because the normal practice of HEP is to publish
standard uncertainty in a normal probability model, as also
recommended by the ISO Guide[3].
In this respect, the ISO recommendation
can be summarized with the following quotation:
``This Guide presents a widely applicable method for
evaluating and expressing uncertainty in measurement.
It provides a realistic rather than a `safe' value of
uncertainty based on the concept that there is no inherent
difference between an uncertainty component arising from a
random effect and one arising from a correction for a
systematic effect. The method stands, therefore, in contrast
to certain older methods that have the following two ideas in
common:
- The first idea is that the uncertainty reported should be `safe'
or `conservative' (
 ) In fact, because the evaluation
of the uncertainty of a measurement result is problematic,
it was often made deliberately large.
) In fact, because the evaluation
of the uncertainty of a measurement result is problematic,
it was often made deliberately large.
- The second idea is that the influences that give rise to uncertainty
were always recognizable as either
`random' or `systematic' with the two being of different nature;
(...) In fact, the method of combining uncertainty was often
designed to satisfy the safety requirement.''
...
When the value of a measurand is reported, the best estimate of
its value and the best estimate of the uncertainty of that estimate
must be given, for if the uncertainty is to err,
it is not normally possible
to decide in which direction
it should err safe. An understatement of uncertainties might cause too
much trust to be placed in the values reported, with sometimes embarrassing
and even disastrous consequences.
A deliberate overstatement of uncertainty could also have undesirable
repercussions.''
The examples of the `undesirable repercussions' given by the ISO
Guide are of the metrological type. In my opinion there are
other physical reasons which should be considered.
Deliberately overstating uncertainty leads to a better
(but artificial)
agreement between results and `known' values or results of other
experiments. This prevents the identification of possible systematic
effects which could have biased the result and which can only be
identified by performing the measurement of the same physical quantity
with a different instrument, method, etc. (the so-called `reproducibility
conditions'[3]). Behind systematic effects there is always some
physics, which can somehow be `trivial' (noise, miscalibration,
row approximations, background, etc.), but also some new phenomenology.
If the results of different experiments are far beyond their
uncertainty the experimenters could compare their methods,
find systematic errors
and, finally, the combined result will be of a higher quality.
In this respect, a quotation from Feynman is in order:
``Well, QED is very nice and impressive, but when everything
is so neatly wrapped up in blue bows, with all
experiments in exact agreement with each other and with
the theory - that is when one is learning
absolutely nothing.''
``On the other hand, when experiments are in hopeless conflict
- or when the observations do not make sense according to
conventional ideas, or when none of the new models seems
to work, in short when the situation is an unholy mess -
that is when one is really making hidden progress
and a breakthrough is just around the corner!''
(R. Feynman, 1973 Hawaii Summer Institute,
cited by D. Perkins at the 1995 EPS Conference, Brussels).




Next: Assessment of uncertainty is
Up: Conclusions
Previous: About subjective probability and
Contents
Giulio D'Agostini
2003-05-15