



Next: Recovering standard methods and
Up: A probabilistic theory of
Previous: Bayes' theorem for uncertain
Contents
Doubtless, many readers could be at a loss at
having to accept that scientific conclusions
may depend on prejudices about the value of a physical quantity
(`prejudice' currently has a negative meaning,
but in reality it simply means
`scientific judgement based on previous
experience'). We shall have many opportunities to enter
again into discussion about this problem,
but it is important to give
a general overview now and to make some firm statements
on the role of priors.
- First, from a theoretical point of view,
it is impossible to get rid of priors; that is if we want
to calculate the probability of events of practical interest, and not just
solve mathematical games.
- At a more intuitive level,
it is absolutely reasonable to draw conclusions in the light of
some reason, rather than in a purely automatic way.
- In routine measurements the interval of prior acceptance
of the possible values is so large, compared to the
width of the likelihood (seen as a function of
 ), that, in practice, it
is as if all values were equally possible. The prior is then
absorbed into the normalization constant:
), that, in practice, it
is as if all values were equally possible. The prior is then
absorbed into the normalization constant:
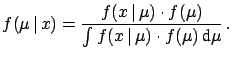 prior very vague prior very vague![$\displaystyle ]{}{f(x\,\vert\,\mu)}.$](img149.png) |
(2.1) |
- If, instead, this is not the case, it is absolutely legitimate to believe
more in personal prejudices than in empirical data.
This could be
when one uses an instrument of which one is not
very confident, or when one does for the first time measurements in
a new field, or in a new kinematical domain, and so on.
For example, it is easier to believe that a student has made a
trivial mistake than to conceive that
he has discovered a new physical effect.
An interesting case
is mentioned by Poincaré [6]:
``The impossibility of squaring the circle was shown in 1885,
but before that date all geometers considered this impossibility
as so `probable' that the Académie des Sciences rejected without
examination the, alas! too numerous memoirs on this
subject that a few unhappy madmen sent in every year.
Was the Académie wrong? Evidently not, and it knew perfectly
well that by acting in this manner it did not run the least risk
of stifling a discovery of moment. The Académie could not have
proved that it was right, but it knew quite well that its instinct
did not deceive it. If you had asked the Academicians, they would
have answered: `We have compared the probability that an unknown
scientist should have found out what has been vainly sought for so
long, with the probability that there is one madman the more
on the earth, and the latter has appeared to us the greater.'''
In conclusion, contrary to those who try to find
objective priors which would give the Bayesian
theory a nobler status of objectivity,
I prefer to state
explicitly the naturalness
and necessity of subjective priors[22].
If rational people (e.g. physicists),
under the guidance of coherency (i.e. they
are honest), but each with unavoidable
personal experience, have priors which are so different
that they reach divergent conclusions,
it just means that
the data are still not sufficiently solid to
allow a high degree of intersubjectivity
(i.e. the subject is still in the area of
active research rather than in that of
consolidated scientific culture). On the other
hand, the step from abstract objective rules
to dogmatism is very short[22].
Turning now to the more practical aspect of presenting
a result, I
will give some recommendations about
unbiased ways of doing this, in
cases when priors are really critical (Section ![[*]](file:/usr/lib/latex2html/icons/crossref.png) ).
Nevertheless, it should be clear that:
).
Nevertheless, it should be clear that:
- since the natural conclusions should be probabilistic
statements on physical quantities, someone has
to turn the likelihoods into probabilities, and
those who have done the experiment are usually the best
candidates for doing this;
- taking the spirit of publishing unbiased results
-- which is in principle respectable -- to extremes,
one should not publish any result,
but just raw data tapes.




Next: Recovering standard methods and
Up: A probabilistic theory of
Previous: Bayes' theorem for uncertain
Contents
Giulio D'Agostini
2003-05-15
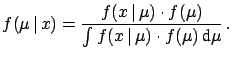 prior very vague
prior very vague