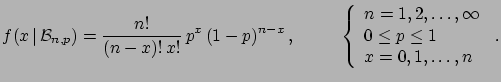Next: Continuous variables: probability and
Up: Random variables
Previous: Random variables
Contents
Uncertain numbers are numbers in respect of which
we are in a condition of uncertainty. They can be the
number associated with the outcome of a die, to the number
which will be read on a scale when a measurement
is performed, or to the numerical
value of a physics quantity. In the sequel, we will
call uncertain numbers also ``random variables'',
to come close to what physicists are used to, but one should
not think, then, that ``random variables'' are only associated
with the outcomes of repeated experiments.
Stated simply, to define a random variable  means to find a rule which allows a real number
to be related univocally
(but not necessarily biunivocal)
to an event (
means to find a rule which allows a real number
to be related univocally
(but not necessarily biunivocal)
to an event ( ).
One could write this expression
).
One could write this expression
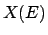 .
Discrete variables assume a countable range, finite or not.
We shall indicate
the variable
with
.
Discrete variables assume a countable range, finite or not.
We shall indicate
the variable
with  and
its numerical realization
with
and
its numerical realization
with  ;
and differently from
other notations, the symbol
;
and differently from
other notations, the symbol  (in place of
(in place of  or
or 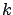 ) is also used for discrete variables.
) is also used for discrete variables.
Here is a list of definitions, properties and notations:
- Probability function:
-
To each possible value of  we associate a degree of belief:
we associate a degree of belief:
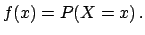 |
(4.1) |
 , being a probability, must satisfy the following properties:
, being a probability, must satisfy the following properties:
- Cumulative distribution function:
-
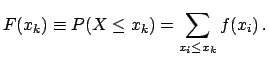 |
(4.5) |
Properties:
- Expectation value (mean):
-
 E E![$\displaystyle [X] = \sum_i x_i f(x_i)\,.$](img395.png) |
(4.10) |
In general, given a function  of
of  ,
,
E![$\displaystyle [g(X)] = \sum_i g(x_i) f(x_i)\,.$](img397.png) |
(4.11) |
E![$ [\cdot]$](img398.png) is a linear operator:
is a linear operator:
E![$\displaystyle [a X+b] = a$](img399.png) E E![$\displaystyle [X] + b \,.$](img400.png) |
(4.12) |
- Variance and standard deviation:
-
Variance:
Standard deviation:
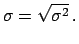 |
(4.14) |
Transformation properties:
- Binomial distribution:
-
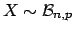 (hereafter ``
(hereafter ``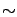 '' stands for ``follows'');
'' stands for ``follows'');
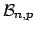 stands for binomial with parameters
stands for binomial with parameters
 (integer) and
(integer) and 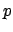 (real):
(real):
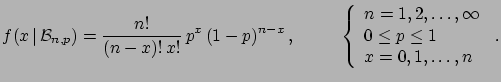 |
(4.17) |
Expectation value, standard deviation and variation coefficient:
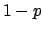 is often indicated by
is often indicated by 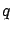 .
.
- Poisson distribution:
-
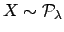 :
:
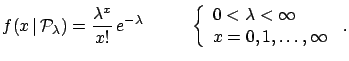 |
(4.21) |
( is an integer,
is an integer,  is real.)
is real.)
Expectation value, standard deviation and variation coefficient:
- Binomial
 Poisson:
Poisson:
-




Next: Continuous variables: probability and
Up: Random variables
Previous: Random variables
Contents
Giulio D'Agostini
2003-05-15
 we associate a degree of belief:
we associate a degree of belief:
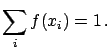
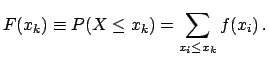
 ,
,
![$\displaystyle [g(X)] = \sum_i g(x_i) f(x_i)\,.$](img397.png)
![]() (hereafter ``
(hereafter ``![]() '' stands for ``follows'');
'' stands for ``follows'');
![]() stands for binomial with parameters
stands for binomial with parameters
![]() (integer) and
(integer) and ![]() (real):
(real):
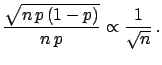
![]() :
:
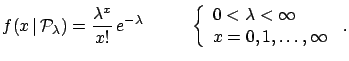
![$\displaystyle [X] = \sum_i x_i f(x_i)\,.$](img395.png)