True value, error and uncertainty

Let us start with case A. A first objection would be ``What does it mean that uncertainties are due to errors? Isn't this just tautology?''. Well, the nouns `error' and `uncertainty', although currently used almost as synonyms, are related to different concepts. This is a first hint that in this subject there is neither uniformity of language, nor of methods. For this reason the metrological organizations have recently made great efforts to bring some order into the field[1,2,3,4,5]. In particular, the International Organization for Standardization (ISO) has published a ``Guide to the expression of uncertainty in measurement''[3], containing definitions, recommendations and practical examples. Consulting the `ISO Guide' we find the following definitions.

• Uncertainty: ``a parameter, associated with the result of a measurement, that characterizes the dispersion of the values that could reasonably be attributed to the measurement.''
• Error: ``the result of a measurement minus a true value of the measurand.''

One has to note the following.

• The ISO definition of uncertainty defines the concept; as far as the operative definition is concerned, they recommend the `standard uncertainty', i.e. the standard deviation (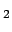$\sigma$) of the possible values that the measurand may assume (each value is weighted with its `degree of belief' in a way that will become clear later).
• It is clear that the error is usually unknown, as follows from the definition.
• The use of the article `a' (instead of `the') when referring to `true value' is intentional, and rather subtle.

Also the ISO definition of true value differs from that of standard textbooks. One finds, in fact:

• true value: ``a value compatible with the definition of a given particular quantity.''

This definition may seem vague, but it is more practical and pragmatic, and of more general use, than ``the value obtained after an infinite series of measurements performed under the same conditions with an instrument not affected by systematic errors." For instance, it holds also for quantities for which it is not easy to repeat the measurements, and even for those cases in which it makes no sense to speak about repeated measurements under the same conditions. The use of the indefinite article in conjunction with true value can be understood by considering the first item on the list in the next section.