Bayes theorem and Bayes factor
The `probabilistic inversion'
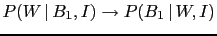 can only3 be performed
using
the so-called Bayes' theorem, a simple consequence
of the fact that, given the effect
can only3 be performed
using
the so-called Bayes' theorem, a simple consequence
of the fact that, given the effect 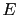 and some
hypotheses
and some
hypotheses 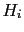 concerning its possible cause,
the joint probability of
concerning its possible cause,
the joint probability of 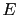 and
and 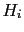 ,
conditioned by the background
information4
,
conditioned by the background
information4
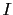 , can be written as
, can be written as
where ` ' stands for a logical `AND'.
From the second equality of the last
equation we get
' stands for a logical `AND'.
From the second equality of the last
equation we get
that is one of the ways to express Bayes'
theorem.5
Since a similar expression holds for
any other hypothesis 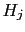 ,
dividing member by member the two expressions
we can restate the theorem in terms of the
relative beliefs, that is
,
dividing member by member the two expressions
we can restate the theorem in terms of the
relative beliefs, that is
the initial ratio of beliefs (`odds') is updated by the
so-called Bayes factor, that depends on how likely
each hypothesis can produce that effect.6Introducing 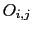 and
BF
and
BF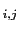 ,
with obvious meanings, we can rewrite
Eq. (4) as
,
with obvious meanings, we can rewrite
Eq. (4) as
Note that, if the initial odds are unitary, than
the final odds are equal to the updating factor. Then, Bayes factors
can be interpreted as odds due only to an individual
piece of evidence, if the two hypotheses were
considered initially equally
likely.7
This allows us to rewrite
BF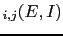 as
as
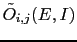 , where the tilde is to remind that they
are not properly odds, but rather
`pseudo-odds'. We get then an expression in which all terms
have virtually uniform meaning:
, where the tilde is to remind that they
are not properly odds, but rather
`pseudo-odds'. We get then an expression in which all terms
have virtually uniform meaning:
If we have only two hypotheses, we get simply
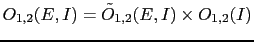 .
If the updating factor is unitary, then the piece of
evidence does not modify our opinion on the two hypotheses
(no matter how small can numerator and denominator be,
as long as their ratio remains finite and unitary! - see Appendix G
for an example worked out in details);
when
.
If the updating factor is unitary, then the piece of
evidence does not modify our opinion on the two hypotheses
(no matter how small can numerator and denominator be,
as long as their ratio remains finite and unitary! - see Appendix G
for an example worked out in details);
when
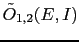 vanishes, then
hypothesis
vanishes, then
hypothesis 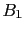 becomes impossible
(``it is falsified''); if instead it is infinite
(i.e. the denominator vanishes), then it is the other
hypothesis to be impossible. (The undefined case
becomes impossible
(``it is falsified''); if instead it is infinite
(i.e. the denominator vanishes), then it is the other
hypothesis to be impossible. (The undefined case 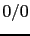 means that we have to look for other hypotheses
to explain the effect.8)
means that we have to look for other hypotheses
to explain the effect.8)
Giulio D'Agostini
2010-09-30
![]() ,
dividing member by member the two expressions
we can restate the theorem in terms of the
relative beliefs, that is
,
dividing member by member the two expressions
we can restate the theorem in terms of the
relative beliefs, that is