The question of how relative frequencies of occurrence
follow from beliefs is much easier. It is
a simple consequence of probability theory and can
be easily understood by anyone familiar with the binomial
distribution, taught in any elementary course on probability.
If we think at 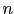 independent trials, for each of which
we believe that the `success' will occur with probability
independent trials, for each of which
we believe that the `success' will occur with probability 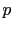 ,
the expected number of successes is
,
the expected number of successes is 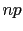 , with
a standard uncertainty
, with
a standard uncertainty
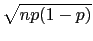 .
We expect then a relative frequency
.
We expect then a relative frequency 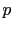 [that is
[that is 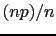 ]
with an uncertainty
]
with an uncertainty
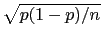 [that is
[that is
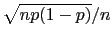 ]. When
]. When 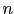 is very large,
the uncertainty goes to zero and
we become `practically sure' to observe a relative frequency
very close to
is very large,
the uncertainty goes to zero and
we become `practically sure' to observe a relative frequency
very close to 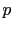 . This asymptotic feature goes under the name
of Bernoulli theorem. It is important to remark that
this reasoning
can be purely hypothetical and has nothing to do
with the so called frequentistic definition of probability.
. This asymptotic feature goes under the name
of Bernoulli theorem. It is important to remark that
this reasoning
can be purely hypothetical and has nothing to do
with the so called frequentistic definition of probability.
To conclude this section, probabilities can be evaluated from
(past) frequencies and (future, or hypothetical)
frequencies can be evaluated from probabilities, but
probability is not frequency.42
Giulio D'Agostini
2010-09-30