Let us go back to our toy model of section 2
and let us complicate it just a little bit, adding the possibility
of incorrect testimony (but we also simplify it
using uniform priors, so that we can focus
on the effect of the uncertain evidence).
For example, imagine you do not see
directly the color of the ball, but this is reported to you by
a collaborator, who, however, might not tell you always the truth.
We can model the possibility of a lie in following way:
after each extraction he tosses a die and reports the true
color only if the die gives a number smaller than 6.
Using the formalism
of Appendix I, we have
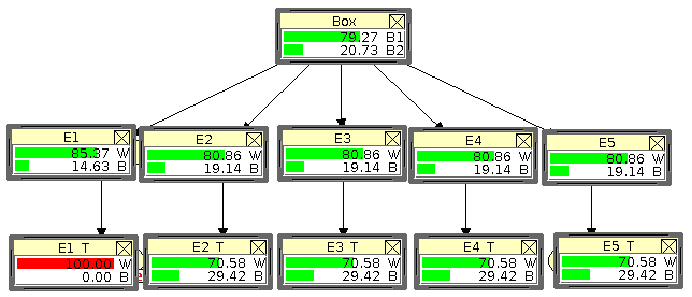
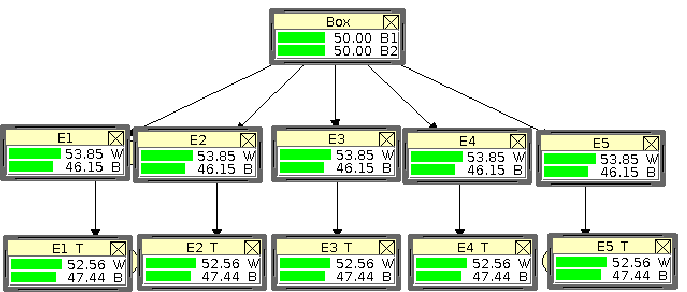
The resulting belief network,64relative to five extractions and
to the corresponding five reports is shown in
figure 2,
redrawn in a different way
in figure 11.
Figure:
Same belief network of figure 2.
This representation shows the `monitors' giving the initial probabilities
of all states of the variables. If you like to test your intuition,
try the guess how all probabilities change when the information
changes in the following order: a) witness 1 says white (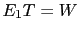 );
b) witness 2 also reports white (
);
b) witness 2 also reports white (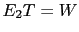 ); c) then witness 3
claims, contrary to the previous two, to have observed
black (
); c) then witness 3
claims, contrary to the previous two, to have observed
black (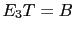 );
c) finally we directly observe the result of the fourth extraction, resulting black
(
);
c) finally we directly observe the result of the fourth extraction, resulting black
(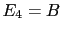 ). The solutions are in figures 13 to
16.
). The solutions are in figures 13 to
16.
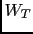 |
In this diagram
the nodes are represented by `monitors' that
provide the probability of each state of the variable.
The green bars mean that we are in condition of uncertainty
with respect to all states of all variable.
Let us describe the several nodes:
- Initial box compositions have probability 50% each,
that was our assumption.
- The probability of white and black are the same for all
extractions, with white a bit more probable than black
(14/26 versus 12/26, that is 53.85% versus 46.15%).
- There is also higher probability that the `witness' reports
white, rather than black, but the difference is attenuated by
the `lie factors'.65
In fact, calling
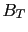 and
and 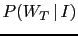 the reported
colors we have
the reported
colors we have
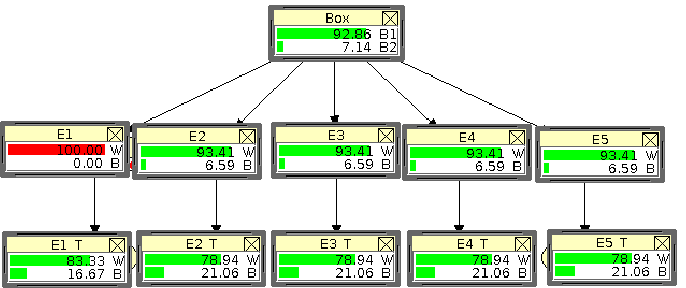
Let us now see what happens if we observe white
(red bar in figure 12).
Figure:
Status of the network after the observation
of a white ball.
 |
All probabilities of the network have been updated
(Hugin [12] has nicely done the job
for us66).
We recognize the 93% of box 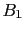 , that we already know.
We also see that the increased belief on this box makes
us more confident to observe white balls in the following
extractions (after re-introduction).
, that we already know.
We also see that the increased belief on this box makes
us more confident to observe white balls in the following
extractions (after re-introduction).
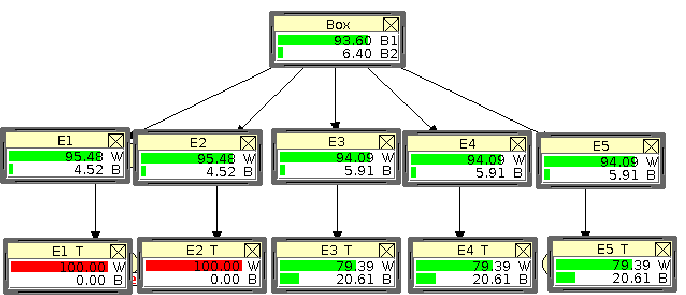
More interesting is the case in which our inference
is based on the reported color (figure 13).
Figure:
Status of the network after the report
of a white ball (compare with figure 12).
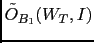 |
The fact that the witness could lie reduces,
with respect to the previous case, our confidence
on 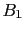 and on white balls
in future extractions. As an exercise on what we have learned
in appendix H, we can evaluate the `effective' Bayes factor
and on white balls
in future extractions. As an exercise on what we have learned
in appendix H, we can evaluate the `effective' Bayes factor
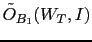 that takes into account the testimony.
Applying Eq. (41) we get
that takes into account the testimony.
Applying Eq. (41) we get
or
 JL
JL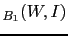 , about a factor of two
smaller than
, about a factor of two
smaller than
 JL
JL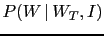 , that was 1.1
(this mean we need two pieces of evidence of this kind
to recover the loss of information due to the testimony).
, that was 1.1
(this mean we need two pieces of evidence of this kind
to recover the loss of information due to the testimony).
The network gives us also the probability that the witness
has really told us the truth, i.e.
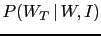 , that is
different from
, that is
different from
 , the reason being that
white was initially a bit more probable than black.
, the reason being that
white was initially a bit more probable than black.
Let us see now what happens if we get two concording testimonies
(figure 14).
Figure:
Network of figure 13 updated
by a second testimony in favor of white.
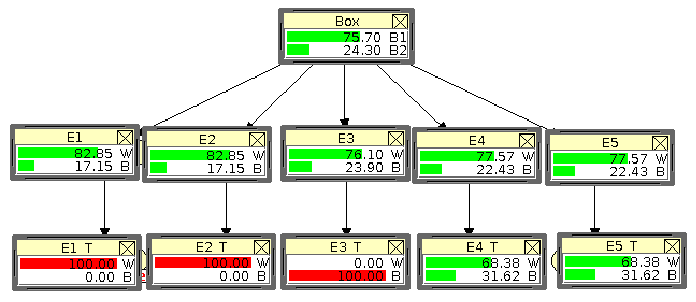 |
As expected, the probability of 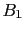 increases and becomes
closer to the case of a direct observation of white.
As usual, also the probabilities of future white balls increase.
increases and becomes
closer to the case of a direct observation of white.
As usual, also the probabilities of future white balls increase.
The most interesting thing that comes from the
result of the network is how the probabilities
that the two witness lie change. First we see that they are the same,
about 95%, as expected for symmetry. But the surprise is that
the probability the the first witness said the truth has increased,
passing from 85% to 95%. We can justify the variation
because, in qualitative agreement with intuition, if we have
concordant witnesses, we tend to believe to each of them more
than what we believed individually. Once again, the result is,
perhaps after an initial surprise, in qualitative agreement with
intuition. The important point is that intuition is unable to
get quantitative estimates. Again, the message is that,
once we agree on the basic assumption and we check, whenever it
is possible, that the results are reasonable, it is better to rely on
automatic computation of beliefs.
Let's go on with the experiment and suppose
the third witness says black
(figure 15).
Figure:
Network of figure 14 updated
by a third testimony in favor of black.
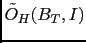 |
This last information reduces the probability of 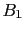 ,
but does not falsify this hypothesis,
as if, instead, we had observed black.
Obviously, it does also reduce the probability of white balls in the
following extractions.
,
but does not falsify this hypothesis,
as if, instead, we had observed black.
Obviously, it does also reduce the probability of white balls in the
following extractions.
The other interesting feature concerns the probability that each
witness has reported the truth. Our belief that the previous
two witnesses really saw what they said
is reduced to 83%. But, nevertheless we are more confident on
the first two witnesses than on the third one,
that we trust only at 76%,
although the lie factor is the same for
all of them. The result is again in agreement with intuition:
if many witnesses state something and fewer say the opposite,
we tend to believe the majority, if we initially consider
all witnesses equally reliable.
But a Bayesian network
tells us also
how much we have to believe the many more then the fewer.
Let us do, also in this case the exercise of calculating the
effective Bayes factor, using however the first formula
in footnote 63:
the effective odds
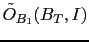 can be written as
can be written as
i.e.
![$ {1}/{[1/13 + (12/13)/(1/5)]} = {13}/{61} = 0.213$](img569.png) ,
smaller then 1 because they provide an evidence
against box
,
smaller then 1 because they provide an evidence
against box 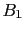 (
(
 JL
JL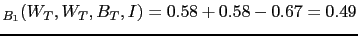 ). It is also easy to check that the
resulting probability of 75.7% of
). It is also easy to check that the
resulting probability of 75.7% of 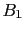 can be obtained
summing up the three weights of evidence, two in favor of
can be obtained
summing up the three weights of evidence, two in favor of
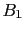 and two against it:
and two against it:
 JL
JL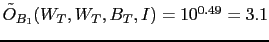 , i.e.
, i.e.
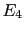 , that
gives a probability of
, that
gives a probability of 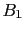 of 3.1/(1+3.1)=76%.
of 3.1/(1+3.1)=76%.
Finally, let us see what happens if we really see a black ball
(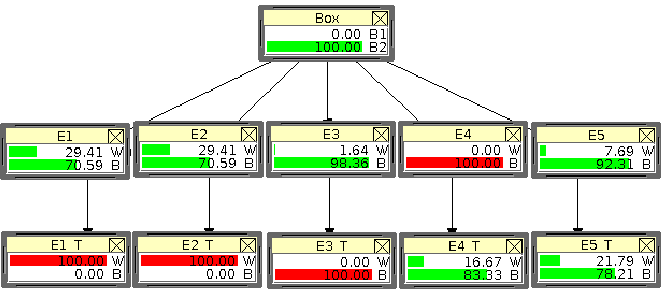 in figure 16).
in figure 16).
Figure:
Network of figure 15 updated
by a direct observation of a black ball.
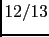 |
Only in this case we become certain that the box is of the kind
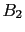 , and the game is, to say, finished. But, nevertheless,
we still remain in a state on uncertainty with respect to several
things. The first one is the probability of a white ball in future
extractions, that, from now becomes
1/13, i.e. 7.7%, and does not change any longer.
But we also remain uncertain on whether the witnesses
told us the truth, because what they said is not
incompatible with the box composition. But, and again in qualitative
agreement with the intuition, we trust much more whom told
black (1.6% he lied) than the two who told white (70.6% they lied).
, and the game is, to say, finished. But, nevertheless,
we still remain in a state on uncertainty with respect to several
things. The first one is the probability of a white ball in future
extractions, that, from now becomes
1/13, i.e. 7.7%, and does not change any longer.
But we also remain uncertain on whether the witnesses
told us the truth, because what they said is not
incompatible with the box composition. But, and again in qualitative
agreement with the intuition, we trust much more whom told
black (1.6% he lied) than the two who told white (70.6% they lied).
Another interesting way of analyzing the final network is to consider
the probability of a black ball
in the five extractions considered.
The fourth is one, because we have seen it. The fifth is 92.3% ()
because we know the box composition. But in the
first two extractions the probability
is smaller than it (70.6%), while in the third is higher (98.4%). That is
because in the two different cases
we had an evidence respectively against and in favor of them.
Giulio D'Agostini
2010-09-30
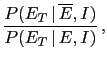
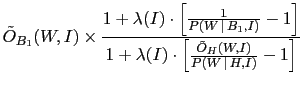
![$\displaystyle \tilde O_{B_1}(W,I) \times
\frac{1 + \lambda(I) \cdot \left[
\fra...
...\lambda(I) \cdot \left[
\frac{ \tilde O_{H}(W,I)}{P(W\,\vert\,H,I)} -1
\right]}$](img558.png)
![]() , that is
different from
, that is
different from
 , the reason being that
white was initially a bit more probable than black.
, the reason being that
white was initially a bit more probable than black.
![]() can be written as
can be written as
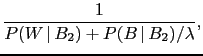
 in figure 16).
in figure 16).