As it is becoming rather well known, the only sound
way to solve what Poincaré called
“the essential problem of the experimental method”
is to tackle it using probability theory, as it should be rather
obvious for “a problem in the probability of causes”.
The mathematical tool to perform what is also known
as `probability inversion' is called
Bayes rule (or theorem),
although due to Laplace, at least in one of the most common
formulations:1
where 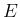 is the observed event and
is the observed event and
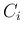 are its possible causes, forming a complete class
(i.e. exhaustive and mutually exclusive).
`
are its possible causes, forming a complete class
(i.e. exhaustive and mutually exclusive).
`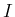 ' stands for the background state of information,
on which all probability evaluations do depend
(`
' stands for the background state of information,
on which all probability evaluations do depend
(`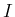 ' is often implicit, as it will be later in this paper,
but it is important to remember
of its existence).
' is often implicit, as it will be later in this paper,
but it is important to remember
of its existence).
Considering also an alternative cause 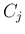 ,
the ratio of the two posterior probabilities,
that is how the two hypotheses are re-ranked
in degree of belief,
in the light of the observation
,
the ratio of the two posterior probabilities,
that is how the two hypotheses are re-ranked
in degree of belief,
in the light of the observation 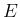 , is given by
, is given by
in which we have factorized the r.h. side into
the initial ratio of probabilities
of the two causes (second term) and the updating factor
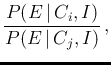 |
|
|
(3) |
known as Bayes factor, or
`likelihood ratio'.2The advantage of
Eq. (2) with respect to Eq. (1)
is that it highlights the two contributions to the posterior
ratio of the hypothesis of interest:
the prior
probabilities of the `hypotheses',
on which there could be a large variety of opinions;
the ratio of the probabilities of the observed event,
under the assumption to each hypothesis of interest,
which can often be rather intersubjective,
in the sense that there is usually a larger, or unanimous
consensus, if the conditions under they have been evaluated
(`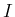 ')
are clearly stated and shared (and in critical cases
we have just to rely on the well argued and documented opinion
of experts.3)
')
are clearly stated and shared (and in critical cases
we have just to rely on the well argued and documented opinion
of experts.3)
Recently, going after years through
the third section of the second
`book' of Gauss' Theoria motus corporum coelestium in sectionibus
conicis solem ambientum [7,8],
of which I had read with the due care only the part
in which the Prince Mathematicorum derives in his
peculiar way what is presently known as the Gaussian (or `normal')
error function,
I have realized that Gauss had also illustrated, a few pages before,
a theorem on how to update the probability ratio of two
alternative hypotheses, based on experimental observations.
Indeed the theorem is not exactly Eq.(2), because
it is only formulated for the case in which
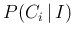 and
and
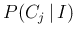 are equal,
but the reasoning Gauss had setup would have led naturally
to the general case. It seems that he focused
into the sub-case of a priori equally likely hypotheses
just because he had to apply his result to a problem
in which he consider the values to be inferred
a priori equally likely
(“valorum harum incognitarum
ante illa observationes aeque probabilia fuisse”).
are equal,
but the reasoning Gauss had setup would have led naturally
to the general case. It seems that he focused
into the sub-case of a priori equally likely hypotheses
just because he had to apply his result to a problem
in which he consider the values to be inferred
a priori equally likely
(“valorum harum incognitarum
ante illa observationes aeque probabilia fuisse”).
But let us proceed in order.
![]() ,
the ratio of the two posterior probabilities,
that is how the two hypotheses are re-ranked
in degree of belief,
in the light of the observation
,
the ratio of the two posterior probabilities,
that is how the two hypotheses are re-ranked
in degree of belief,
in the light of the observation ![]() , is given by
, is given by
![]() and
and
![]() are equal,
but the reasoning Gauss had setup would have led naturally
to the general case. It seems that he focused
into the sub-case of a priori equally likely hypotheses
just because he had to apply his result to a problem
in which he consider the values to be inferred
a priori equally likely
(“valorum harum incognitarum
ante illa observationes aeque probabilia fuisse”).
are equal,
but the reasoning Gauss had setup would have led naturally
to the general case. It seems that he focused
into the sub-case of a priori equally likely hypotheses
just because he had to apply his result to a problem
in which he consider the values to be inferred
a priori equally likely
(“valorum harum incognitarum
ante illa observationes aeque probabilia fuisse”).