- ...
formulations:1
- “The greater the probability of an observed event
given any one of a number of causes to which that event may be attributed,
the greater the likelihood of that cause
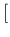 given that event
given that event![$]$](img6.png) .
The probability of the existence of any one of these causes
.
The probability of the existence of any one of these causes
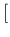 given the event
given the event![$]$](img6.png) is thus a fraction
whose numerator is the probability of the event given the cause,
and whose denominator is the sum of similar probabilities,
summed over all causes.
If the various causes are not equally probable
a priory, it is necessary, instead of the probability of the event
given each cause, to use the product of this probability
and the possibility
of the cause itself.”[1]
is thus a fraction
whose numerator is the probability of the event given the cause,
and whose denominator is the sum of similar probabilities,
summed over all causes.
If the various causes are not equally probable
a priory, it is necessary, instead of the probability of the event
given each cause, to use the product of this probability
and the possibility
of the cause itself.”[1]
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ratio'.2
- The
alternative name likelihood ratio is preferred
in some communities of researchers
because numerator
and denominator of Eq. (3) are called likelihood
by statisticians.
My preference to `Bayes factor' (or even Bayes-Turing Factor
[2,3,4]) is due to the fact
that, since in the common parlance `likelihood' and `probability'
are in practice equivalent, `likelihood ratio'
tends to generate confusion as it were the ratio of the probabilities
of the hypotheses of interest (and the value that maximizes the
`likelihood function' tends to be considered by itself
the most probable value).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... experts.3
- For example the
European Network of Forensic Science Institutes
strongly recommends [5] forensic scientists to report
the `likelihood ratio' of the findings in the light
of the hypothesis of the prosecutor and the hypothesis
of the defense, abstaining to assess which hypothesis
they consider more probable, task left to the judicial
system (but then I have strong worries, shared by other
researchers, about the ability of the members of
judicial system of making
the proper use of such a quantitative information!).
To those interested on the details of how
this Guideline can be turned into practice,
a Coursera offered by the University of Lausanne
is recommended [6]
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... whatever”.4
- All English quotes
are taken from the C.H. Davis translation [8].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... `articles' 5
- This publication is divided into two `books',
each of them subdivided in four `sections'. Then the entire
text is divided
in numeri (translated into `articles' by Davies [8])
running through the `books'. In particular, Section 3 of Book 2,
consisting of 22 printed pages in the original Latin edition,
contains `articles' 172 to 189.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...ascends 6
- “...ad disquisitionem
generassimam in omni calculi ad philosophiam naturalem applicatione
fecundissima ascendemus.”
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... times):7
- For
the reader' convenience (hopefully)
the functions are called here, except when they appear in quotes,
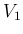 ,
, 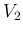 ,
, 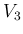 , etc.,
and the measured values
, etc.,
and the measured values 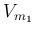 ,
, 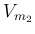 ,
, 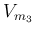 , etc.,
while Gauss uses
, etc.,
while Gauss uses 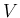 ,
, 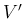 ,
, 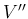 ...and
...and
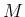 ,
, 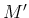 ,
, 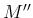 ..., respectively.
..., respectively.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
function8
- Note how Gauss
simply speaks of `probabilities',
obviously meaning probability
density functions, as clear from the
use he makes of them: “the probability to be assigned
to each error
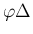 will be expressed by a function of
will be expressed by a function of 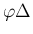 that we shall denote as
that we shall denote as
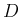 ” - a few lines later it is
clear that Gauss had in mind a 'pdf' since, when he wrote
“the probability generally, that the error lies between
” - a few lines later it is
clear that Gauss had in mind a 'pdf' since, when he wrote
“the probability generally, that the error lies between 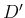 and
and 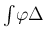 ,
will be given by the integral
,
will be given by the integral
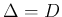 d
d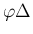 extended
from
extended
from 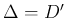 to
to
 ”.
”.
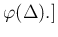 Note also that in the case a function had only one argument,
parentheses were not used. Therefore
Note also that in the case a function had only one argument,
parentheses were not used. Therefore
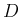 stands
for
stands
for
![$\varphi(\Delta).]$](img57.png)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... function.9
- For
an account of Gauss' derivation in modern notation
see Sec. 6.12 of Ref. [9]
(some intermediate steps needed to reach the solution
are sketched in
http://www.roma1.infn.it/~dagos/history/Gauss_Gaussian.pdf).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...Therefore,10
- As clarified in footnote 8, it is
clear that in the following quotes the generic term
“probability” stands for probability density function.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... functions.11
- The
reason why in the argument appears the differences and not simply
the observed values is that for Gauss
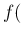 was the error
function, i.e. `probability density function' of the errors
(see also footnote 8). Since, later in `article' 177,
the function
was the error
function, i.e. `probability density function' of the errors
(see also footnote 8). Since, later in `article' 177,
the function 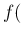 will become the `Gaussian' error function,
we could rewrite directly the joint pdf of the observations
in modern notation
as
will become the `Gaussian' error function,
we could rewrite directly the joint pdf of the observations
in modern notation
as
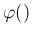
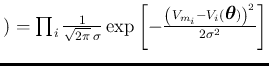
![$) = \prod_i\frac{1}{\sqrt{2\pi}\,\sigma}
\exp\left[-\frac{\left(V_{m_i}-V_i(\mbox{\boldmath$\theta$})\right)^2}{2\sigma^2}\right]$](img76.png) .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... before12
- The historian of statistics
Stephen Stigler refers to Laplace's 1774 Mémoire
as “arguably the most influential article this field
[mathematical statistics
 ] to appear before 1800,
being the first widely read presentation of inverse probability
and its application to both binomial and location
parameter estimation.” [11]
(note that in this reference there is no mention to Gauss).
] to appear before 1800,
being the first widely read presentation of inverse probability
and its application to both binomial and location
parameter estimation.” [11]
(note that in this reference there is no mention to Gauss).
 As far as I know, neither Gauss nor Laplace were
using the word `statistics', but they were talking about probability.
As far as I know, neither Gauss nor Laplace were
using the word `statistics', but they were talking about probability.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... fuisse”).13
- It is clear that what is unknown are the
numeric values of the quantities
and not the `quantities' themselves, at it could seem from the English
translation, because
in that case
there would be little to infer.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... i.e.14
- Note:
the reason of using in the formulae
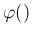
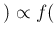
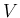 , instead
than just
, instead
than just
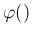 is simply due to the way Gauss wrote the error function,
but, obviously, this function could be redefined and
is simply due to the way Gauss wrote the error function,
but, obviously, this function could be redefined and
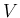 would disappear
from the above equations, then getting for example
would disappear
from the above equations, then getting for example
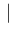
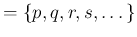
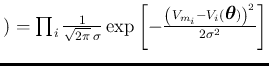
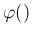
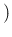
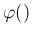
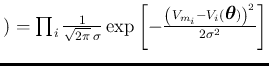
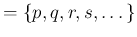
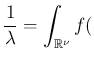 ,
as we would write it nowadays
(see also footnote 11).
,
as we would write it nowadays
(see also footnote 11).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
theorem.15
- Indeed Ref. [13] cites
Ref. [14], writing which I had realized
that Gauss was using a `Bayesian reasoning',
but I had at that time completely skipped
the `details' in which he derived, as a theorem,
the rule to update the ratio of probabilities of hypotheses,
subject of this paper.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... follow,16
- For example
he derived the formula of the weighted average, stressing its
importance to use it, instead of the individual
values [12].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
reading.17
- Historical French and German translations
are also available [15,16].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... else?18
- Although the formal theory
of probability has only been developed in the last few centuries,
the noun probabilitas, the adjective
probabilis and especially its comparative probabilior
(`more probable'), playing a fundamental
role in probabilistic reasoning,
were used in Latin with essentially the
same meaning we assign to them in ordinary language.
For example, a recent `grep' through the Cicero texts collected
in The Latin Library [17] resulted in
105 words containing `probabil'. And it is rather popular
the Cicero's quote “Probability is the very guide
of life” [18], although such a sentence
does not appears verbatim in his texts, but it is a digest of his
thought (see e.g. De Natura Deorum, Liber Primus,
nr. 12 [17]).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
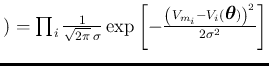
 ] to appear before 1800,
being the first widely read presentation of inverse probability
and its application to both binomial and location
parameter estimation.” [11]
(note that in this reference there is no mention to Gauss).
] to appear before 1800,
being the first widely read presentation of inverse probability
and its application to both binomial and location
parameter estimation.” [11]
(note that in this reference there is no mention to Gauss).
 As far as I know, neither Gauss nor Laplace were
using the word `statistics', but they were talking about probability.
As far as I know, neither Gauss nor Laplace were
using the word `statistics', but they were talking about probability.
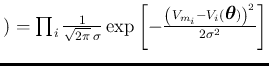
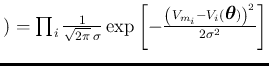
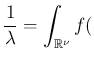 ,
as we would write it nowadays
(see also footnote 11).
,
as we would write it nowadays
(see also footnote 11).